
题目列表(包括答案和解析)
4.已知等腰 的腰为底的2倍,则顶角
的腰为底的2倍,则顶角 的正切值是
(D )
的正切值是
(D )
(A) (B)
(B)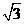 (C)
(C) (D)
(D)
3.答案:B。导析:由 可得
可得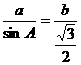 ,由正弦定理可知
,由正弦定理可知 ,故可得
,故可得 ,故
,故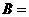
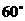 或
或 。
。
3.在 中,若
中,若 ,则
,则 等于 ( )
等于 ( )
A.
 B.
B. 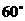 C.
C.  或
或 D.
D. 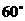 或
或
2.答案:A。 导析:利用正弦定理可得:

2.在△ABC中,若 ,则
,则 与
与 的大小关系为( A)
的大小关系为( A)
)
A. 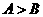 B.
B.  C.
C.  ≥
≥ D.
D.  、
、 的大小关系不能确定
的大小关系不能确定
1.答案:D。导析:利用正弦定理直接可以求得,要注意解的个数问题。
1.已知△ABC中,a=4,b=4 ,∠A=30°,则∠B等于( D )
,∠A=30°,则∠B等于( D )
A.30° B.30°或150°
C.60° D.60°或120°
1. 在问题1.中我们已经知道已知两边及其中一边的对角解三角形时,其余的一边两角不是唯一确定,那如果已知三角形的任意两角与一边,求其它两边和一角的情况怎样呢?这种情况下会有几解呢?
解析:在三角形ABC中,如果已知A,B和b,那C是唯一确定的,利用正弦定理可以发现a,c只有一解,因此如果已知三角形的任意两角与一边,求其它两边和一角只有一种情况,只有一解。
典例导思:
考查目标一:已知三角形两角及其中一角的对边求解三角形。
典例1.已知:在 中,
中, ,
, ,
, ,解此三角形。
,解此三角形。
导拨:在该题中,已知C及c,可以利用正弦定理列出方程进行求解。
解析:由 ,
, 可得
可得
由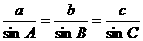 ,可依次计算出
,可依次计算出 ,
,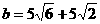 。
。
规律总结:已知三角形两角及其中一角的对边求解三角形这种情况只有一种,处理方法主要借助于正弦定理解方程,在求方程的过程中我们要分清角及其角的对边,搞清楚各个量之间的关系。
考查目标二:已知三角形两边及其中一边的对角求解三角形。
典例2.已知下列三角形的两边及其一边的对角,判断三角形的情况,有解的作出解答。
(1)a=7,b=9,A=100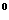 (2)a=10,b=20,A=75
(2)a=10,b=20,A=75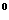
(3)a=10,c=5 ,C=60
,C=60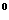 (4)a=2
(4)a=2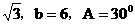
导拨:已知三角形两边及其中一边的对角求解三角形的有可能有两种情况,具体有几解可以借助于《疑难导析》1中的方法解决。
解析:(1) 本题无解。
本题无解。
(2) 本题无解。
本题无解。
(3)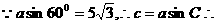 本题有一个解。
本题有一个解。
利用正弦定理,可得:
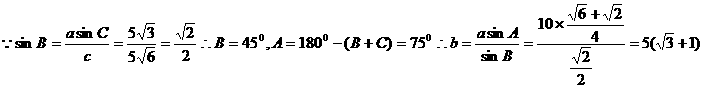 (4)
(4) 本题有两解。
本题有两解。
由正弦定理得:
当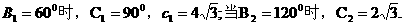
综上所述:
规律总结:已知三角形两边及其中一边的对角求解三角形的有可能有两种情况,具体方法可以借助于下了表格:
|
|
A为钝角 |
A为直角 |
A为锐角 |
|
|
a>b |
一解 |
一解 |
一解 |
|
|
a=b |
无解 |
无解 |
一解 |
|
|
a<b |
无解 |
无解 |
a>bsinA |
两解 |
|
a=bsinA |
一解 |
|||
|
A<bsinA |
无解 |
在线拓展:已知:在 中,
中, ,
, ,
, ,解此三角形。
,解此三角形。
解析:由
∴当 时,
时, 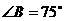 ∴
∴
∴当 时,
时, 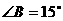 ∴
∴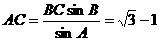 。
。
考察目标三:求三角形面积。
典例3:在 的面积。
的面积。
导拨:已知三角形两边及其一边的对角,由正弦定理来解题。
解析:根据正弦定理有
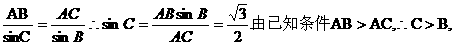 则C有两解。
则C有两解。
(1)当C为锐角时,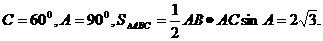
(2)当C为钝角时,
所以, 的面积为
的面积为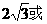

规律总结: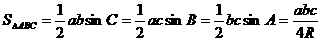 (R为三角形外接圆半径)
(R为三角形外接圆半径)
公式中需要知道两边及其夹角,在此题目中需要求出A,而对于A有两种情况,因此该三角形的面积有两解。
考查目标四:正弦定理的综合应用。
典例4:如右图,D是直角 斜边BC上的一点,AB=AD,记
斜边BC上的一点,AB=AD,记
(1)
证明:sin (2)若AC=
(2)若AC= ,求
,求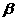 的值。
的值。
导拨:结合已知条件,利用诱导公式找出角及角的三角函数间关系。
解析:(1)证明: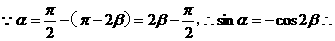 sin
sin 。
。
(2) 在三角形ADC中,由正弦定理可得:

 sin
sin
在(1)中sin ,
,

解得:sin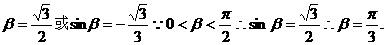


规律总结:正弦定理揭示了任意三角形边角之间的客观关系,是解三角形的重要工具,它经常与三角函数,平面向量知识在三角形中有密切的联系。
分级导练:
基础巩固:
1.已知两边及其中一边的对角解三角形时,其余的一边两角是否唯一确定呢?情况怎样呢?
解析:在 中,已知a,b和A,以点C为圆心,以边长a为半径画弧,此弧与除去顶点A的射线AB的公共点的个数即为三角形解的个数,解的个数见下表:
中,已知a,b和A,以点C为圆心,以边长a为半径画弧,此弧与除去顶点A的射线AB的公共点的个数即为三角形解的个数,解的个数见下表:
(1) A为锐角时:
|


(2)A为直角或钝角时:


由上可见,已知两边及其中一边的对角解三角形时,其余的一边两角不是唯一确定,可以用下表标:
|
|
A为钝角 |
A为直角 |
A为锐角 |
|
|
a>b |
一解 |
一解 |
一解 |
|
|
a=b |
无解 |
无解 |
一解 |
|
|
a<b |
无解 |
无解 |
a>bsinA |
两解 |
|
a=bsinA |
一解 |
|||
|
A<bsinA |
无解 |
3.利用正弦定理体现了三角形中边角之间的关系,那么能否利用正弦定理与三角形的面积有何关系呢?
 解析:①
解析:①
如右图,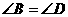 ,所以
,所以
所以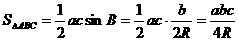
即三角形面积公式为:
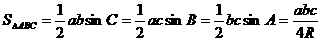 (R为三角形外接圆半径)
(R为三角形外接圆半径)
疑难导析:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com