4．在各类广告中，我们会经常遇到由“方便样本(即样本没有代表性”所产生的结论。例如“现代研究证明，99%以上的人感染有螨虫，”请你从统计学的角度分析该数据的产生情况，如果样本是从去医院看皮肤病的人中产生，那么样本具有代表性吗？

[拓展尝新]

3．某班有50名学生，要从中随机地抽取6人参加一项活动，请用抽签法和随机数表法进行抽取，并写出具体过程。

2．简单随机抽样的常用方法有_________和_____________。当随机地选定随机数表读数选定开始读数的数后，读数的方向可以是________________________________。

1．在简单抽样中，某一个个体被抽的可能是　　　　　　　　　　　　 (　　 )

A．与第几次抽样有关，第一次抽中的可能性大些。

B．与第几次抽样无关，每次抽中的可能性相等。

C．与第几次抽样有关，最后一次抽中的可能性较大。

D．与第几次抽样无关，每次都是等可能的抽取，但各次抽取的可能不一样。

2．经典回放：

例1： 1936 年， 美国著名的 «文学摘要»杂志社,为了预测总统候选人罗斯福与兰登两人谁能当选,他们以电话簿上的地址和俱乐部成员名单上的地址发出1000万封信,收回回信200万封,在调查史上这是少有的样本容量,花费了大量的人力、物力，«文学摘要»相信自己的调查结果，即兰登将以57%对43%的比例获胜，并进行大量宣传，最后选举却是罗斯福以62%对38%的巨大优势获胜，这个调查断送了这家原本颇有名气的杂志社的前程，不久只得关门停刊，试分析这次调查失败的原因。

分析：科学地选取样本是对样本进行数据分析的前提。

解：失败的原因：(1)抽样方法不公平，样本不具有代表性，样本不是从总体(全体美国公民)中随机地抽取的，当年，美国有私人电话和参加俱乐部的家庭都是比较富裕的家庭，1929-1933年的世界经济危机，使美国经济遭到打击，“罗斯福新政”动用行政手段干预经济，损害了部分富人的利益，“喝了富人的血”，但广大的美国人民从中得到了好处，所以，从富人中抽取的样本严重偏离了总体。 　(2)样本容量相对过小，也是导致估计出现偏差的重要原因，因为样本容量越大，估计才能准确，发出的信不少，但回收率太低。 点评：数理统计中涉及到两个问题： 　1、研究如何抽样，抽多少，怎样抽，才能使样本具有很好的代表性，这是抽样方法问题； 　2、研究如何对样本进行合理的分析，作出科学的推断，怎样用样本估计总体。 　　 本例中，调查失败的根本原因就是抽样方法不合理，造成样本不具有代表性。样本的性质不能反映总体的性质，我们所说的随机抽样并不是“随便抽样”，“随意抽样”，在抽样的过程中，要保证抽样的公平性，等可能性的同时，还要保证所抽样本具有较好的代表性，要能反映出总体的特征，这样，我们才能通过研究样本来估计总体。要保证所抽样本中有穷人，也有富人，不同阶层的人按比例抽取，这样得到的样本才能较全面地反映总体，得到的结果才具有参考意义。　

例2 ：现有30个零件，需从中抽取10个进行检查，问如何采用简单随机抽样得到一个容量为10的样本？

　分析： 简单随机抽样适合总体个数较少的情况，本题中总体个数只有30个，所以具有可行性。

　解法一(抽签法)：先将30个零件编号：1，2，3，…，30，并把号码写在形状，大小相同的号签上(号签可以用小球、卡片、纸条等制作)，然后将这30个号签放在同一个箱子里，进行均匀搅拌。抽签时，每次从中抽出1个号签，连续抽10次，就得到一个容量为10的样本。

　解法二(随机数表法)：

　第一步，将30个零件编号00，01，02，…，29。

　第二步，在随机数表中任选一数开始，如从第7行第9的数06开始。

　第三步，从06开始向右读，读到88>29，删去；继续向右读，得到04，将它取出；继续下去，又得到21，25，12，随后的两位数号码是06，由于它前面已取出，将它去掉；再继续下去，又得到01，16，19，10，07。至此，10个样本的号码已取得。于是，所要抽取的样本号码是：

　06，04，21，25，12，01，16，19，10，07。

　点评： 使用随机数表法时，选取开始读的数是任意的，读数的方向也是随机的，可以向右，也可以向左，向上或向下等。在每两位地读数过程中，得到一个两位数字号码，在去掉其中不合要求和与前面重复的号码后，其中依次出现的号码可以看成是依次从总体中抽取的各个个体的号码。

[同步训练]

1．解析视屏：

　数理统计学的核心问题是如何根据样本的情况对总体的情况作出一种推断。这里包括两

类问题：一类是如何从总体中抽取样本；另一类是如何根据对样本的整理、计算和分析，对

总体的情况作出判断。科学合理地抽取样本是对总体进行分析的前提。

简单随机抽样是在特定总体中抽取样本，总体中每一个个体被抽取的可能性是等同的，而且任何个体之间彼此被抽取的机会是独立的。如果用从个体数为N的总体中抽取一个容量为n的样本，那么每个个体被抽取的可能性等于。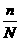　　

简单随机抽样在本章既是重点又是难点。简单随机抽样是抽样中最简单的一种模型，它是本节另两种抽样方法，乃至更复杂的抽样方法的基础。

　(1)关于简单随机抽样的定义，我们可以从以下几个方面来理解。

　①它要求被抽取样本的总体的个体数有限。这样，就便于对其中各个个体被抽取的可能性进行分析。

　②它是从总体中逐个地进行抽取。这样，就便于在抽样实践中进行操作。

　③它是不放回抽样。由于抽样实践中多采用不放回抽样，使其具有较广泛的实用性，而且由于所抽取的样本中没有被重复抽取的个体，便于进行有关的分析和计算。

　④它是一种等可能抽样。不仅每次从总体中抽取一个个体时，各个个体被抽取的可能性相等，而且在整个抽样过程当中，各个个体被抽取的可能性相等，从而保证了这种抽样方法的公平性。

　(2)进行简单随机抽样，从含有N个个体的总体中抽取一个容量为n的样本时，在整个抽样过程中每个个体被抽取的可能性都相等，即等于。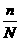

　(3)实施简单随机抽样，主要有两种方法：抽签法和随机数表法。

　抽签法比较简单。对于随机数表法我们首先要理解随机数表并不惟一；其次，只要符合各个位置上等可能地出现其中各个数的要求，就可以构成随机数表。一般来说，统计工作者常用计算机来生成随机数表。

　利用随机数表进行抽样时，应按照如下三个步骤：

　第一步，将总体中的个体编号(由于需要编号，如果总体中的个体数目太多，采用随机表法进行抽样就显得不太方便了)。这里的所谓编号，实际上是编数字号码。例如将100个个体编号成：00，01，02，…，99。而不是编号成：0，1，2，…，99。此外，将起始号码选为00，而不是01，可使100个个体都可用两位数字号码表示，以便于运用随机数表。

　第二步，选定开始的数字。为了保证所选定数字的随机性，应在面对随机数表之前就指出开始数字的纵横位置。

　第三步，获取样本号码。为了便于操作，特别是为了知道所抽取的每一个号码是否与前

面得到的号码重复，可将总体中所有个体的数字号码先按顺序列出，每抽出一个号码，就在

列出的号码中做一个记号，这样就知道后面得到的号码是否曾被取出，最后做了记号的这些

号码就可以看成是依次从总体中抽取的各个个体的号码。

2．　 学法指导：

统计的特征之一是通过部分的数据来推测全体数据的性质, 体会统计结果具有随机性，

统计推断是有可能犯错误的，感受统计思维与确定性思维的不同。统计思维和确定性思维一样成为人们不可缺少的思想武器。

[教师在线]

1．学习目标：

(1)理解简单随机抽样的概念，会用简单随机抽样(抽签法、随机数表法)从总体中抽取

样本。

　 (2)初步感受收集数据的科学性对决策所起的作用。

5．解:(1)分段:362/40商是9余数为2,抽样距为9;(2)先用简单抽样从这些书中抽取2册书不检验;(3)将剩下的书编号:0,1,…,359;(4)从第一组(编号为0,1,…,8)书中按照简单随机抽样的方法抽取一册书,比如其编号为k;(5)顺序地抽取编号为下面数字的书:k+9n(1≤n≤39),总共得到40个样本。

1．系统抽样，00037，001037，00237，00337，00437，99537，99637，99737，99837，99937。 2．，样本， 3．C 4．同例2