
题目列表(包括答案和解析)
20.解:(1)由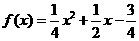 ,
,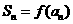 ,
,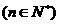
得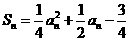
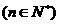 ①
………2分
①
………2分
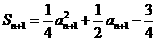 ,
②
,
②
即 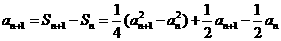 , ………4分
, ………4分
即 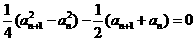 ,
,
即 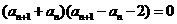

20.(本题满分14分)设函数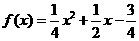 ,对于正数数列
,对于正数数列 ,其前
,其前 项和为
项和为 ,且
,且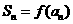 ,
,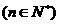 .
.
(1)求数列 的通项公式;
的通项公式;
(2)是否存在等比数列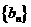 ,使得
,使得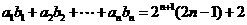 对一切正整数
对一切正整数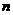 都成立?若存在,请求出数列
都成立?若存在,请求出数列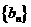 的通项公式;若不存在,请说明理由.
的通项公式;若不存在,请说明理由.
19.(本题满分14分)已知二次函数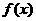 的二次项系数为
的二次项系数为 ,且不等式
,且不等式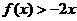 的解集为
的解集为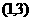 。(1)若方程
。(1)若方程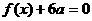 有两个相等的根,求
有两个相等的根,求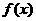 的解析式;
的解析式;
(2)若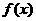 的最大值为正数,求a的取值范围.
的最大值为正数,求a的取值范围.
解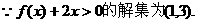
∴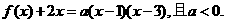 …………2分
…………2分
∴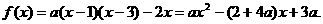 ①
①
由方程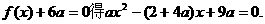 ② …………4分
② …………4分
因为方程②有两个相等的根,所以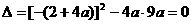 ,
,
即  …………6分
…………6分
由于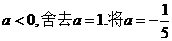 代入①得
代入①得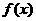 的解析式
的解析式
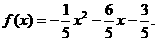 …………7分
…………7分
(Ⅱ)由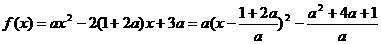 …………9分
…………9分
及 …………10分
…………10分
由 解得
解得 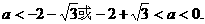 …………13分
…………13分
故当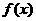 的最大值为正数时,实数
的最大值为正数时,实数 的取值范围是
的取值范围是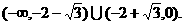 …………14分
…………14分
18.(本题满分13分)已知等比数列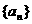 的各项都是正数,前
的各项都是正数,前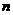 项和为
项和为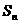 ,且
,且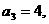
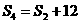 ,求:(1)首项
,求:(1)首项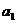 及公比
及公比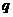 的值;(2)若
的值;(2)若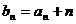 ,求数列
,求数列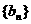 的前
的前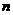 项和
项和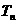 。
。
解:(1)由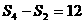 ,得
,得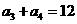 ,则
,则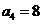 …………3分
…………3分
故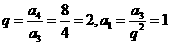 …………6分
…………6分
(2)由(1)数列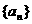 的首项为1,公比为2,所以
的首项为1,公比为2,所以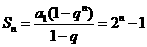 …8分
…8分
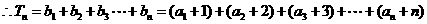
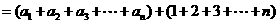
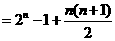 …………12分
…………12分
故数列数列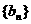 的前
的前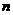 项和
项和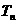 为
为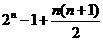 。
…………13分
。
…………13分
17、(本题满分13分)经过长期观测得到:在交通繁忙的时段内,某公路段汽车的车流量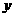 (千辆/小时)与汽车的平均速度
(千辆/小时)与汽车的平均速度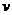 (千米/小时)之间的函数关系为:
(千米/小时)之间的函数关系为: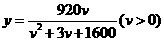 .
.
(1) 在该时段内,当汽车的平均速度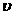 为多少时,车流量最大?最大车流量为多少?
为多少时,车流量最大?最大车流量为多少?
(保留分数形式)
(2) 若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内?
解:(Ⅰ)依题意,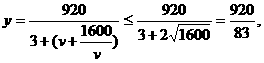 ……………3 分
……………3 分
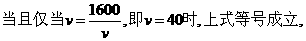 ……5 分
……5 分
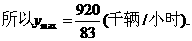 ……6分
……6分
故当v=40千米/小时,车流量最大,最大车流量约为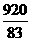 11.1千辆/小时. ……7分
11.1千辆/小时. ……7分
(Ⅱ)由条件得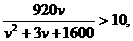
整理得v2-89v+1600<0,………………………………………………9分
即(v-25)(v-64)<0,
解得25<v<64. ……………………………………………………….;12分
若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应大于25千米/小时且小于64千米/小时.………………………13分
16.(本题满分13分)某纺纱厂生产甲、乙两种棉纱,已知生产甲种棉纱1吨需耗一级子棉2吨、二级子棉1吨;生产乙种棉纱1吨需耗一级子棉1吨、二级子棉2吨。每吨甲种棉纱的利润是600元,每吨乙种棉纱的利润是900元。若工厂在生产这两种棉纱的计划中要求消耗一级子棉不超过300吨、二级子棉不超过250吨,则甲、乙两种棉纱应各生产多少吨,才能使利润总额最大?
1解:设生产甲、乙两种棉纱各 吨,利润总额为
吨,利润总额为 元,则目标函数
元,则目标函数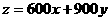 ,
,
 且
且 满足条件
满足条件
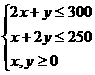 ,
…………3分
,
…………3分
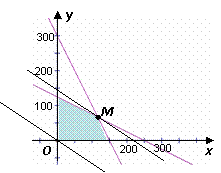
可行域如图中阴影部分所示。 …………5分
把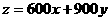 变形为
变形为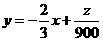 ,得到斜率为
,得到斜率为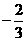 ,在
,在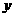 轴上的截距为
轴上的截距为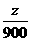 ,随
,随 变化的一族平行直线。 …………7分
变化的一族平行直线。 …………7分
由图可知,当直线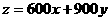 经过可行域上的点M时,截距
经过可行域上的点M时,截距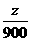 最大,即利润
最大,即利润 有最大值。
…………9分
有最大值。
…………9分
由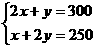 得点M的坐标为
得点M的坐标为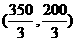 ,
…………11分
,
…………11分
所以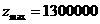 。
…………12分
。
…………12分
故当生产甲棉纱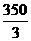 吨、乙棉纱
吨、乙棉纱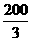 时,利润总额有最大值1300000元。…………13分
时,利润总额有最大值1300000元。…………13分
15.(Ⅰ)解:在 中,
中,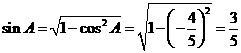 ,…………2分
,…………2分
由正弦定理,得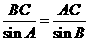 .
…………4分
.
…………4分
所以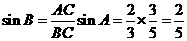 .
…………6分
.
…………6分
(Ⅱ)解:因为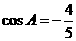 ,所以角
,所以角 为钝角,从而角
为钝角,从而角 为锐角,于是
为锐角,于是
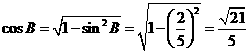 ,
…………8分
,
…………8分
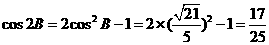 ,
,
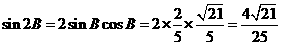 .
…………10分
.
…………10分
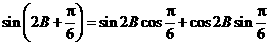
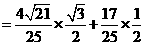
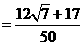 . …………13分
. …………13分
温馨提示: 考生请注意在答题卷规定区域内用黑色笔作答,超出指定区域答题不给分.
15.(本题满分13分)在 中,已知
中,已知 ,
,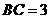 ,
,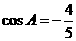 .
.
(Ⅰ)求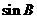 的值;
的值;
(Ⅱ)求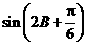 的值.
的值.
14.若数列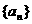 满足
满足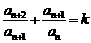 (
(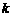 为常数),则称数列
为常数),则称数列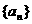 为等比和数列,k称为公比和.已知数列
为等比和数列,k称为公比和.已知数列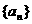 是以3为公比和的等比和数列,其中
是以3为公比和的等比和数列,其中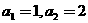 ,则
,则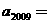 .
.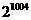
13.若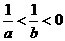 ,则下列不等式:①
,则下列不等式:①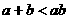 ;②
;②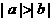 ;③
;③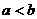 ;④
;④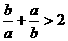 中,正确的不等式有 (填序号)①④
中,正确的不等式有 (填序号)①④
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com