22．箱子中装有6张卡片，分别写有1到6这6个整数. 从箱子中任意取出一张卡片，记下它的读数，然后放回箱子，第二次再从箱子中取出一张卡片，记下它的读数，

试求：(1)是5的倍数的概率；

(2)是3的倍数的概率；

(3)中至少有一个5或6的概率。

21．一台机器由于使用时间较长，生产的零件有一些会有缺损．按不同转速生产出来的零件有缺损的统计数据如下：

转速(转/s)	16	14	12	8
每小时生产有缺损零件数(件)	11	9	8	5

(1)作出散点图；

(2)求线性回归方程；

(3) 如果实际生产中，允许每小时的产品中有缺损的零件最多为10个，那么机器运转速度应控制在什么范围内？

19．高三年级有500名学生，为了了解数学学科的学习情况，现从中随机抽出若干名学生在一次测试中的数学成绩，制成如下频率分布表：

(1)根据右面图表，求①②③④处的数值;

分组	频数	频率
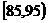	①	②
		0．050
		0．200
	12	0．300
		0．275
	4	③
[145，155]		0．050
合计	④

(2)根据题中信息估计总体平均数.

　 20．已知数列中，，且 ，求这个数列的第m项的值.现给出此算法流程图的一部分

(1)　　　 请将空格部分(两个)填上适当的内容；

(2)　　　 用“For”循环语句写出对应的算法；

(3)　　　 若输出S=16，则输入的的值是多少？

18．在某地的奥运火炬传递活动中，有编号为1，2，3，，18的18名火炬手.若从中任选3人，则选出的火炬手的编号能组成3为公差的等差数列的概率为________．

17．设集合，且在直角坐标平面内，从所有满足这些条件的有序实数对所表示的点中任取一个，其落在圆内的概率恰为，则的一个可能的正整数值是________(只需写出一个即可)．

16．甲乙两人约定在6时到7时之间在某处会面，并约定先到者等候另一人15分钟，过时即可离去，则两人会面的概率是____________．

15．在样本的频率分布直方图中，共有4个长方形，这4个小长方形的面积由小到大构成等差数列，已知，且样本容量为400，则小长方形面积最大的一组的频数为______________ ．

14．已知总体的各个体的值由小到大依次为2，3，3，7，a，b，12，13.7，18.3，20，且总体的中位数为10.5．若要使该总体的方差最小，则a、b的取值分别是_________．

13．若从集合的所有子集中任取一个子集，则取出的集合含有至少两个元素的概率是_______________．

12．某算法的伪代码如图所示，如果输出的

y值是4，那么输入的x的所有可能的

值是___________.