
题目列表(包括答案和解析)
1.一条直线和两异面直线b,c都相交,则它们可以确定( )
A.一个平面 B.两个平面
C.三个平面 D.四个平面
13.证明:(Ⅰ)连结AC,则 是
是 的中点,在△
的中点,在△ 中,EF∥PA…………………………3分
中,EF∥PA…………………………3分
且PA 平面PAD,EF
平面PAD,EF 平面PAD,∴EF∥平面PAD…………………………………6分
平面PAD,∴EF∥平面PAD…………………………………6分
(Ⅱ)因为平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,又CD⊥AD,所以CD⊥平面PAD,
∴CD⊥PA……………………………………………………………………………………9分
又PA=PD= AD,所以△PAD是等腰直角三角形,且
AD,所以△PAD是等腰直角三角形,且 ,即PA⊥PD……………12分
,即PA⊥PD……………12分
而CD∩PD=D,∴ PA⊥平面PDC,又EF∥PA,所以EF⊥平面PDC………………………14分
12.(1)证明:连接AC,设AC∩BD=O.由条件得ABCD为正方形,故O为AC中点.因为E为CC1中点,所以OE∥AC1.因为OEÌ平面BDE,AC1(/平面BDE.所以AC1∥平面BDE.
(2)连接B1E.设AB=a,则在△BB1E中,BE=B1E=a,BB1=2a.所以BE2+B1E2=BB12.所以B1E^BE.由正四棱柱得,A1B1^平面BB1C1C,所以A1B1^BE.所以BE^平面A1B1E.所以A1E^BE.同理A1E^DE.所以A1E^平面BDE.
10. (1)取 中点
中点 ,连结
,连结 ,
,

 分别为
分别为 的中点,
的中点,
 ,且
,且
又 正三棱柱
正三棱柱 ,
,
 四边形
四边形 为平行四边形。
为平行四边形。


所以 
(1) 由可得,取 中点
中点
 正三棱柱
正三棱柱 ,
,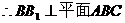 。
。
 平面
平面 ,
, ,
,
 为
为 的中点,
的中点, ,
, 
 ,
, 
 ,
,



 ,
,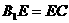




4. 5。 ②③ 6。
5。 ②③ 6。 7。1或2 8。
7。1或2 8。 9。异面
9。异面
3.如图,两个正方形 和
和 所在平面互相垂直,设
所在平面互相垂直,设 、
、 分别是
分别是 和
和 的中点,那么①
的中点,那么①  ;②
;②  面
面 ;③
;③  ;④
;④  、
、 异面
异面
其中正确结论的序号是__①②③___________.
2.已知m,l是直线,α,β是平面,给出下列命题:
①若l垂直于α内的两条相交直线,则l⊥α;
②若l平行于α,则l平行于α内的所有直线;
③四面体中最多可以有四个面是直角三角形;
④若m α且l⊥β, 且α∥β则m
α且l⊥β, 且α∥β则m l
l
其中正确命题的是 ①③④ 。
1.已知直线a、b、l及平面M、N。给出下列四个命题
①若a∥M,b∥M,则a∥b
②若a∥M,b⊥a,则b⊥M
③若a M,b
M,b M,且l⊥a,l⊥b,则l⊥M
M,且l⊥a,l⊥b,则l⊥M
④若a⊥M,a∥N,则M⊥N
其中真命题的序号是______④_______.(将所有正确结论的序号都写上)
13. 如图,在四棱锥
如图,在四棱锥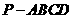 中,底面
中,底面 是正方形,侧面
是正方形,侧面 底面
底面 ,且
,且 ,若
,若 、
、 分别为
分别为 、
、 的中点.(Ⅰ) 求证:
的中点.(Ⅰ) 求证: ∥平面
∥平面 ;
;
(Ⅱ) 求证: 平面
平面 .
.
高二数学立体几何练习一
12.在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为CC1的中点. 求证:(1)AC1∥平面BDE;(2)A1E^平面BDE.(注:正四棱柱侧棱垂
直于底面,底面是正方形)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com