
题目列表(包括答案和解析)
19. (本题满分14分)
设 ,
, 两点在抛物线
两点在抛物线 上,
上, 是
是 的垂直平分线.
的垂直平分线.
(Ⅰ)当且仅当 取何值时,直线
取何值时,直线 经过抛物线的焦点
经过抛物线的焦点 ?证明你的结论;
?证明你的结论;
(Ⅱ)当直线 的斜率为2时,求
的斜率为2时,求 在
在 轴上截距的取值范围.
轴上截距的取值范围.
18. (本题满分14分)
如图,在正三棱柱ABC-A1B1C1中,BB1=BC=2,且M是BC的中点,点N在CC1上.
 (Ⅰ)试确定点N的位置,使AB1⊥MN;
(Ⅰ)试确定点N的位置,使AB1⊥MN;
(Ⅱ)当AB1⊥MN时,求二面角M-AB1-N的大小的余弦值.
17.(本小题满分14分)已知三点 .
.
(Ⅰ)求以 为焦点且过点P的椭圆的标准方程;
为焦点且过点P的椭圆的标准方程;
(Ⅱ)设点 关于直线
关于直线 的对称点分别为
的对称点分别为 求以
求以 为焦点且过点
为焦点且过点 的双曲线的标准方程.
的双曲线的标准方程.
40.00 39.99 39.95 40.0l 40.02 39.98 40.00 39.99 40.00 39.96
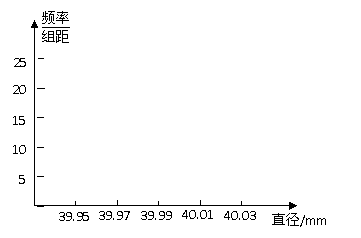
(Ⅰ)完成下面的频率分布表,并画出频率分布直方图;
(2)假定乒乓球的直径误差不超过0.02mm为合格品.若这批乒乓球的总数为10000只,试根据抽样检查结果估计这批产品的合格只数.
|
分 组 |
频数 |
频率 |
|
|
[39.95,39.97) |
|
|
|
|
[39.97,39.99) |
|
|
|
|
[39.99,40.01) |
|
|
|
|
[40.0l,40.03] |
|
|
|
|
合计 |
|
|
|
40.03 40.00 39.98 40.00 39.99 40.00 39.98 40.01 39.98 39.99
16.(本题满分12分)
某制造商为2008年北京奥运会生产一批直径为40mm的乒乓球,现随机抽样检查20只,测得每只球的直径(单位mm,保留两位小数)如下:
15.(本题满分12分)
袋子中有红、白、黄、黑颜色不同大小相同的四个小球.
(Ⅰ)从中任取一球,求取出白球的概率;
(Ⅱ)从中任取两球,求取出的是红球、白球的概率;
((Ⅲ)从中先后各取一球,求先后取出的分别是红球、白球的概率.
14. 已知动点A、B分别在图中抛物线
已知动点A、B分别在图中抛物线 及椭圆
及椭圆
 的实线上运动,若
的实线上运动,若 ∥
∥
 轴,点N的坐标
轴,点N的坐标
为(1,0),则三角形ABN的周长 的取值范围是
.
的取值范围是
.
13.设命题p:|4x-3|≤1;命题:q:x2-(2a+1)x+a(a+1)≤0.若┐p是┐q的必要而不充分条件,则实数a的取值范围是 .
12.椭圆 的焦点为
的焦点为 ,点P为其上动点,当
,点P为其上动点,当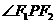 为钝角时,点P横坐标的取值范围是_____________.
为钝角时,点P横坐标的取值范围是_____________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com