…………2分

在中，,由正弦定理

　…………4分

,又　　　　 ……6分

(2)解如图，作交于点D点，连结BD，

由线面垂直的性质定理知　　　　　　　　　　　　 …………8分

为二面角的平面角。　　　　　　　 …………9分

在　　　　　　　　　　　　　　 …………10分

　　　　　　 …………12分

20. (本小题满分10分)

如图，在直三棱柱中， AB=1，

，∠ABC=60.

(Ⅰ)证明：；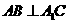

(Ⅱ)求二面角A--B的大小(用三角函数值表示即可)。　　

19.(本小题满分10分)如图，O为坐标原点，过点P(2,0)且斜率为k的直线l交抛物线

于两点.

(1)求与的值；(2)求证：.

(1)解：由题意知直线l的方程为，…………1分

代入抛物线方程消去y，得 　①

　　　　　　　　　　　　　　　　　　　　　　 …………2分

点A,B的横坐标是方程①的两个根，

由韦达定理得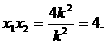　　　　　　　　　　 …………3分

由, , 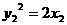　　　　　　　　　　　　…………4分

得　　　　　　　　　　　　　 …………5分

注意到，所以　　　　　　　　　 …………6分

(2)证明：设直线OA,OB的斜率分别为，则，　　　 …………8分

相乘得,所以. 　　　　　　　…………10分

18.(本题满分10分)设f(1)＝2，f(n)>0(nN₊)，且f(n₁+n₂)＝f(n₁)f(n₂)，求的值，试猜想f(n)的解析式，并证明你的猜想。

解：∵f(1)＝2，

∴f(2)＝f(1+1)＝f(1)·f(1)＝f²(1)＝4＝2²

f(3)＝f(1+2)＝f(1)f(2)＝8＝2³，

f(4)＝＝ ＝16＝2⁴，

f(5) ＝＝ ＝32＝2⁵，…………4分

……

猜想：f(n)＝2ⁿ.　　　　　　　　 …………6分

(1)证明：当n＝1时，f(1)＝2显然成立. …………7分

(2)假设n＝k时，f(k)＝2^k

则当n＝k+1时，f(k+1)＝f(k)·f(1)＝2^k·2＝2^k+1，

所以等式成立　　　　　　　　　　　　　　 …………9分

由(1)(2)知，对于任意的正整数n,f(n)＝2ⁿ成立.

　　　　　　　　　　　　　　　　　　　 …………10分

17.(本题满分10分)在长方体中，

已知DA=DC=4,DD₁=3,求异面直线A₁B与B₁C所成角的余弦值。　　　　

[解法一]连接A­₁D，∵A­₁D∥B₁C,

　∴∠BA₁D是异面直线A₁B与B₁C所成的角　　　　　　　　　　　　　　　　 ……4分

连接BD,在△A­₁DB中,AB=A­₁D=5,BD=4 ……6分

cos∠BA₁D=

　　　　 ==　 ……9分

∴异面直线A₁B与B₁C所成角的余弦值是　　　　　　　　 ……10分

[解法二]以D为坐标原点,DA、DC、DD₁所在直线为x轴、y轴、z轴,建立空间直角坐标系.　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ……2分

则A₁(4,0,3) 、B(4,4,0) 、B₁(4,4,3) 、C(0,4,0),

得=(0,4,-3),=( -4,0,-3)　　 ……6分

设与的夹角为θ,

cosθ==　 ……9分

∴异面直线A₁B与B₁C所成角的余弦值是。　　　　　　　　 ……10分

16．将全体正整数排成一个三角形数阵：

1

2　 3

4　 5　 6

7　 8　 9　 10

． ． ． ． ． ． ．

按照以上排列的规律，第10 行从左向右的第3 个数为 　　　　　　．48

[解析]本小题考查归纳推理和等差数列求和公式．前n－1 行共有正整数1+2+…+(n－1)个，即个，因此第n 行第3 个数是全体正整数中第+3个，即为．

[答案]48

15．在平面上，若两个正三角形的边长的比为1：2，则它们的面积比为1：4，类似地，在空间内，若两个正四面体的棱长的比为1：2，则它们的体积比为　　　　　

[解析] 考查类比的方法。体积比为1：8

14．已知椭圆的长轴长是短轴长的2倍，则椭圆的离心率等于　　　　　 　　　　

13.抛物线的准线方程是　　　　　　　 　　

21. (本小题满分12分)已知椭圆C:(a＞b＞0)的离心率为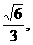短轴一个端点到右焦点的距离为. (Ⅰ)求椭圆C的方程;

(Ⅱ)设直线l与椭圆C交于A、B两点，坐标原点O到直线l的距离为，求△AOB面积的最大值.