
题目列表(包括答案和解析)
1.已知命题 ,
, ,则( )
,则( )
A. ,
, B.
B.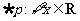 ,
,
C. ,
, D.
D.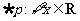 ,
,
10、解:
(1)由已知得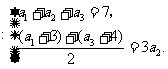 解得
解得 .设数列
.设数列 的公比为
的公比为 ,
,
由 ,可得
,可得 .又
.又 ,可知
,可知 ,
,
即 ,
,
解得 . 由题意得
. 由题意得 .
.  .
.
故数列 的通项为
的通项为 .……………………………6分
.……………………………6分
(2)由于 由(1)得
由(1)得


= ……………..12分
……………..12分
9、(Ⅰ)证明:由题设 ,得
,得 ,
, .
.
又 ,所以数列
,所以数列 是首项为
是首项为 ,且公比为
,且公比为 的等比数列.…………4分
的等比数列.…………4分
(Ⅱ)解:由(Ⅰ)可知 ,于是数列
,于是数列 的通项公式为
的通项公式为
 .所以数列
.所以数列 的前
的前 项和
项和 .…………8分
.…………8分
(Ⅲ)证明:对任意的 ,
,
 .所以不等式
.所以不等式 ,对任意
,对任意 皆成立.…………12分
皆成立.…………12分
7、解:(Ⅰ)设登山组人数为 ,游泳组中,青年人、中年人、老年人各占比例分别为a、b、c,则有
,游泳组中,青年人、中年人、老年人各占比例分别为a、b、c,则有 ,解得b=50%,c=10%.
,解得b=50%,c=10%.
故a=100%-50%-10%=40%,即游泳组中,青年人、中年人、老年人各占比例分别为40%、
50%、10%。
(Ⅱ)游泳组中,抽取的青年人数为 (人);抽取的中年人数为
(人);抽取的中年人数为
 50%=75(人);抽取的老年人数为
50%=75(人);抽取的老年人数为 10%=15(人)。
10%=15(人)。

6、解:根据表中所列数据可得散点图如下:
(2)列出下表,并用科学计算器进行有关计算:
 |
1 |
2 |
3 |
4 |
5 |
 |
2 |
4 |
5 |
6 |
8 |
 |
30 |
40 |
60 |
50 |
70 |
 |
60 |
160 |
300 |
300 |
560 |
因此, 。
。
 ,
,
于是可得:
 ;
;
 。
。
因此,所求回归直线方程为: =1.04x+44.8
=1.04x+44.8
(3)据上面求得的回归直线方程,当广告费支出为10百万元时。
 =1.04×10+44.8=55.2(百万元)
=1.04×10+44.8=55.2(百万元)
即这种产品的销售收入大约为55.2百万元。
5、解:
(Ⅰ) 类工人中和
类工人中和 类工人中分别抽查25名和75名。
......4分
类工人中分别抽查25名和75名。
......4分
(Ⅱ)(ⅰ)由 ,得
,得 ,
,
 ,得
,得 。
。
频率分布直方图如下
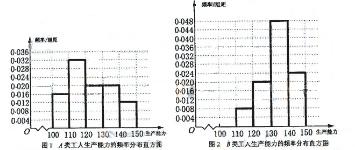 ......8分
......8分
从直方图可以判断: 类工人中个体间的差异程度更小。
......9分
类工人中个体间的差异程度更小。
......9分
(ii) 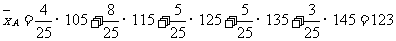 ,
,
 ,
,

 A类工人生产能力的平均数,B类工人生产能力的平均数以及全厂工人生产能力的平均数的估计值分别为123,133.8和131.1.
A类工人生产能力的平均数,B类工人生产能力的平均数以及全厂工人生产能力的平均数的估计值分别为123,133.8和131.1.
4.解:(1)直线方程可化为
直线 的方程的斜率
的方程的斜率
因为 当且仅当
当且仅当 的等号成立。
的等号成立。
 。
。
(2)不能,由(1)知 的方程为
的方程为 ,其中
,其中 圆心
圆心 ,圆心C
,圆心C
到直线 的距离d
的距离d ,由
,由 ,
, ,而
,而 从而,
从而,
若 与圆C相交,则圆C截直线
与圆C相交,则圆C截直线 所得的弦所对立的圆心角小于
所得的弦所对立的圆心角小于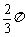 ,所以
,所以 不能将圆C
不能将圆C
分割成弧长的比值为 的两段弧。
的两段弧。
3.(1)由条件

(2)
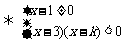
 当
当 时,得
时,得 ,当
,当 时,得
时,得 ,当
,当 时,
时, 。
。
当① ,②
,② ③当
③当
2.解:设 半径为
半径为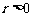 ,C在
,C在 上
上
 ,又C与y轴相切,
,又C与y轴相切,
又在 上截弦长为
上截弦长为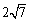 ,则圆心到
,则圆心到 的距离
的距离

 圆C方程为
圆C方程为 或
或
1.(1) 或
或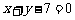
(2)设 的斜率为k,因分别与x,y正半轴相交,所以
的斜率为k,因分别与x,y正半轴相交,所以
则设 则
则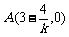

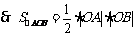


 当且仅当
当且仅当 时,则
时,则 (舍)or
(舍)or

故
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com