
题目列表(包括答案和解析)
2. 设 是空间三条不同的直线,且满足
是空间三条不同的直线,且满足 ,
,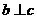 ,则
,则 与
与 的位置关系一定是
的位置关系一定是
A、 与
与 异面
B、
异面
B、
C、 D、
D、
1. 已知直线 的倾斜角
的倾斜角 ,则直线
,则直线 的斜率
的斜率
A、-1 B、1 C、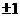 D、不存在
D、不存在
20.(本题满分14分)设数列 满足
满足 ,
, ,
, ,其中
,其中 、
、 为实数,且
为实数,且 .
.
(1)求数列 的通项公式;(4分)
的通项公式;(4分)
(2)设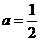 ,
, ,
, ,求数列
,求数列 的前
的前 项的和
项的和 ;(5分)
;(5分)
(3)在(2)的条件下,若存在自然数 使
使 对
对 恒成立,
恒成立,
求 的最小值. (5分)
的最小值. (5分)
解:(1)(1)
 是以
是以 为首项,c为公比的等比数列,
为首项,c为公比的等比数列,

(2)

 ,
,
 得
得


(3)当 时,
时,
 为递增数列,
为递增数列,
 ,
,
 存在自然数
存在自然数 使
使 对
对 恒成立,
恒成立,
 .
.
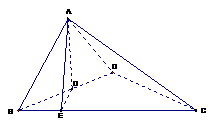
19. (本题14分)如图,四面体ABCD中,O是BD的中点,ΔABD和ΔBCD均为等边三角形,AB =2 , AC =
(本题14分)如图,四面体ABCD中,O是BD的中点,ΔABD和ΔBCD均为等边三角形,AB =2 , AC = .
.
(1)求证: 平面BCD; (4分)
平面BCD; (4分)
(2)求二面角A-BC- D的大小; (5分)
(3)求O点到平面ACD的距离. (5分)
证明:(1)连结OC, 为等边三角形,
为等边三角形, 为
为 的中点,∴
的中点,∴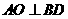 .
.  ,
,
 , ∴
, ∴ .在
.在 中,
中,
 ∴
∴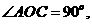 即
即
 ∴
∴ 平面
平面 .
.
(2)过O作 ,连结AE,
,连结AE,
 ,∴AE在平面BCD上的射影为OE.∴
,∴AE在平面BCD上的射影为OE.∴ .∴
.∴  .
.
在 中,
中, ,
,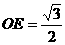 ,
,
 , ∴
, ∴ .
.
∴二面角A-BC-D的大小为 .
.
(3)解:设点O到平面ACD的距离为
 ,
,
∴ .在
.在 中,
中,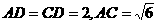 ,
,  .而
.而 ,
,
∴ . ∴点O到平面ACD的距离为
. ∴点O到平面ACD的距离为 .
.
18. (本题10分)已知向量
(本题10分)已知向量 ,
, ,函数
,函数 .(1)求f(x)的最大值及相应的x的值;(5分);(2)若
.(1)求f(x)的最大值及相应的x的值;(5分);(2)若 ,求
,求 的值.(5分)
的值.(5分)
解:(1) ,当
,当
即 时,
时,
(2) ,
, 
17.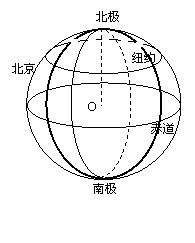 (本题9分)已知地球半径约为6371千米,北京的
(本题9分)已知地球半径约为6371千米,北京的
位置约为东经116°、北纬40°,纽约的位置约为西经74°,
北纬40°.若飞机以平均速度720千米/小时飞行,则从北
京到纽约的最短飞行时间约为多少小时?(飞机飞行高度忽
略不计,结果精确到0.1小时)
解:设北京为点A,纽约为点B,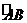 是通过A、B的大圆的劣弧,A、B点的纬线所在的圆的圆心为
是通过A、B的大圆的劣弧,A、B点的纬线所在的圆的圆心为 ,
,
由已知得 ,
, ,
, ,在
,在 中,
中,
 ,
,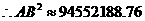 ,
,
在 ,
, ,
, ,
,
 大圆的圆弧
大圆的圆弧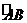 的长为
的长为
 千米 ,
千米 , 小时.答:则从北京到纽约的最短飞行时间约为15.4小时.
小时.答:则从北京到纽约的最短飞行时间约为15.4小时.
16. (本题8分)如图,一个倒置的圆锥形容器的轴截面是边长为4厘米的正三角形,在容器内放一个半径为1厘米的钢球,并将容器倒满水,将钢球取出后,容器内的水深是多少厘米?(精确到0.1).
(本题8分)如图,一个倒置的圆锥形容器的轴截面是边长为4厘米的正三角形,在容器内放一个半径为1厘米的钢球,并将容器倒满水,将钢球取出后,容器内的水深是多少厘米?(精确到0.1).
解:由题意得圆锥的体积为
球的体积为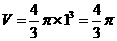
设取出球后的的容器中水的高度为 ,水面的半径为
,水面的半径为 ,则
,则 ,即
,即 ,水的容积为
,水的容积为


 ,
,
答:容器内的水深是3.1厘米.
12、 D ;13、 B ;14、 D ;15 C ;
1、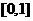 ;2、
;2、 ;3、2或-3;4、
;3、2或-3;4、 ; 5、 6 ;6、
; 5、 6 ;6、 或
或 ;7、
;7、 ;8、
;8、 ;9、
;9、 ;10、 1 ;11、
;10、 1 ;11、 .
.
20.(本题满分14分)设数列 满足
满足 ,
, ,
, ,其中
,其中 、
、 为实数,且
为实数,且 .
.
(1)求数列 的通项公式;(4分)
的通项公式;(4分)
(2)设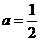 ,
, ,
, ,求数列
,求数列 的前
的前 项的和
项的和 ;(5分)
;(5分)
(3)在(2)的条件下,若存在自然数 使
使 对
对 恒成立,
恒成立,
求 的最小值. (5分)
的最小值. (5分)
2009学年松江二中第一学期高二数学期末试题答题纸2010.01
(请将答案写在答题纸上,写在卷子上无效)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com