
题目列表(包括答案和解析)
4.下列命题错误的是 ( )
A.命题“若 有实数根”的逆否命题为:“若方程
有实数根”的逆否命题为:“若方程 无实数根,则
无实数根,则 ”
”
B.“ ”是“
”是“ ”的充分不必要条件
”的充分不必要条件
C.若 为假命题,则p、q均为假命题
为假命题,则p、q均为假命题
D.对于命题 .
.
3. 在△ABC中,若=,则△ABC的形状是.( )
A.等腰直角三角形 B.直角三角形 C.等腰或直角三角形 D.等边三角形
2. 已知 是等差数列,切
是等差数列,切 则
则 的值是( )
的值是( )
A.117 B.114 C.111 D.108
1. 在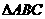 中,A、B的对边分别是
中,A、B的对边分别是 ,且
,且 ,那么满足条件的
,那么满足条件的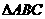 ( )
( )
A.有一个解 B.有两个解 C.无解 D.不能确定
13.(1)F(-c,0),B(0, ),∵kBF=
),∵kBF= ,kBC=-
,kBC=- ,C(3c,0)
,C(3c,0)
且圆M的方程为(x-c)2+y2=4c2,圆M与直线l1:x+ y+3=0相切,
y+3=0相切,
∴
 ,解得c=1,
,解得c=1,
∴所求的椭圆方程为 6分
6分
(2) 点A的坐标为(-2,0),圆M的方程为(x-1)2+y2=4,
过点A斜率不存在的直线与圆不相交,设直线l2的方程为y=k(x+2),
∵ ,又
,又 ,∴cos<
,∴cos< >=
>=
∴∠PMQ=120°,圆心M到直线l2的距离d= ,所以
,所以 ,∴k=
,∴k=
所求直线的方程为x±2 +2=0.
14分
+2=0.
14分
13.如图,F是椭圆 (a>b>0)的一个焦点,A,B是椭圆的两个顶点,椭圆的离心率为
(a>b>0)的一个焦点,A,B是椭圆的两个顶点,椭圆的离心率为 .
.
点C在x轴上,BC⊥BF,B,C,F三点确定的圆M恰好与直线l1: 相切.
相切.
(Ⅰ)求椭圆的方程:
 (Ⅱ)过点A的直线l2与圆M交于PQ两点,且
(Ⅱ)过点A的直线l2与圆M交于PQ两点,且 ,求直线l2的方程.(14分)
,求直线l2的方程.(14分)
12.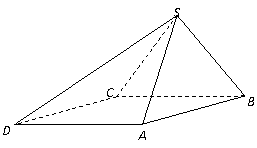 四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.
四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.
已知∠ABC=45°,AB=2,BC= ,SA=SB=
,SA=SB=
(Ⅰ)证明:SA⊥BC;
(Ⅱ)求二面角S-AD-C的正切值;(13分)
(Ⅰ)作 ,垂足为
,垂足为 ,连结
,连结 ,由侧面
,由侧面 底面
底面 ,得
,得 底面
底面 ,得
,得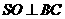
因为 ,所以
,所以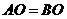 ,
,
 又
又 ,故
,故 为等腰直角三角形,
为等腰直角三角形, ,
,
∴ ,得
,得 .(6分)
.(6分)
(Ⅱ)由(Ⅰ)知 ,依题得
,依题得 ,
,
故 ,
,
∴二面角S-AD-C的平面角为∠SAO
由 ,
, ,得
,得 ,
, ,∴
,∴ (13分)
(13分)
11.已知圆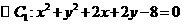 与
与 相交于
相交于 两点,(1)求公共弦
两点,(1)求公共弦 所在的直线方程;
所在的直线方程;
(2)求圆心在直线 上,且经过
上,且经过 两点的圆的方程;(13分)
两点的圆的方程;(13分)
解:(1)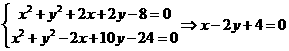 (6分)
(6分)
(2)法1:由(1)得
 ,即A(-4,0),B(0,2),又圆心在直线
,即A(-4,0),B(0,2),又圆心在直线 上,
上,
设圆心为M(x,-x)
则|MA|=|MB|,解得M(-3,3), (13分)
(13分)
法2:圆系法略
10.从棱长为3的正四面体的各顶点截去四个棱长为1的小正四面体(使截面平行于底面),所得几何体的表面积是
.
9.若半径为1的动圆与圆 相切,则动圆圆心的轨迹方程是
.
相切,则动圆圆心的轨迹方程是
.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com