
题目列表(包括答案和解析)
5、设双曲线的焦点在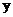 轴上,两条渐近线为
轴上,两条渐近线为 ,则该双曲线的
,则该双曲线的
离心率 ( )
( )
A. B.
B.  C.
C. D.
D.
4、椭圆 的半焦距等于( )
的半焦距等于( )
A. B.
B.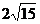 C.
C. D.
D.
3、命题“存在 R,
R,
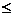 0”的否定是.
0”的否定是.
(A)不存在 R,
R,  >0 (B)存在
>0 (B)存在 R,
R, 
 0
0
(C)对任意的 R,
R, 
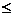 0
(D)对任意的
0
(D)对任意的 R,
R,  >0
>0
2、下列命题的逆否命题中,真命题的个数为( )
(1)若q<1,则方程x2+2x+q=0有实根
(2)若x2+y2=0,则x、y全为零
(3)如果两圆相切,那么圆心距等于两圆半径之和
(4)奇数不能被2整除.
A. 1 B. 2 C. 3 D. 4
1、如果命题 是真命题,命题
是真命题,命题 是假命题,那么( )
是假命题,那么( )
A. 命题p一定是假命题 B. 命题q一定是假命题
C. 命题q一定是真命题 D. 命题q是真命题或假命题
22.(本小题满分14分)
已知椭圆 的焦点在
的焦点在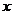 轴上,
轴上, 为坐标原点,
为坐标原点, 是一个焦点,
是一个焦点,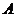 是一个顶点.若椭圆的长轴长是
是一个顶点.若椭圆的长轴长是 ,且
,且 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)求点 与椭圆
与椭圆 上的点
上的点 之间的最大距离;
之间的最大距离;
(Ⅲ)设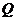 是椭圆
是椭圆 上的一点,过
上的一点,过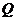 的直线
的直线 交
交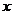 轴于点
轴于点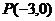 ,交
,交 轴于点
轴于点 .若
.若 ,求直线
,求直线 的斜率.
的斜率.
21.(本小题满分12分)
正方形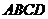 的顶点
的顶点 在抛物线
在抛物线 上,一条对角线
上,一条对角线 在直线
在直线 上, (Ⅰ)求
上, (Ⅰ)求 所在的直线方程.(Ⅱ)求正方形
所在的直线方程.(Ⅱ)求正方形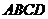 的面积.
的面积.
20.(本小题满分12分)
甲乙两条货船要到同一个泊位装运货物,两船
停泊的时间都为4小时.
(Ⅰ)若它们一天中只是在从凌晨 点到
点到 点的这
点的这 个整数点时刻等可能的到泊位停靠,求一天中,有一条船需要等待的概率;
个整数点时刻等可能的到泊位停靠,求一天中,有一条船需要等待的概率;
(Ⅱ)若它们可以在一天中在从凌晨 点到
点到 点的任何时刻等可能的到泊位停靠,求一天中,有一条船需要等待的概率.
点的任何时刻等可能的到泊位停靠,求一天中,有一条船需要等待的概率.
19. (本小题满分12分)
(本小题满分12分)
如图,四边形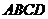 是正方形,
是正方形, 平面
平面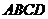 ,
, 平面
平面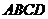 ,
, .
.
(Ⅰ)求证: ∥平面
∥平面 ;
;
(Ⅱ)求证:平面 ⊥平面
⊥平面 .
.
18.(本小题满分12分)
小张在工厂实习50天,每天生产的零件数可用茎叶图表示如下:
|
1 |
3 4 5 6 6
6 7 8 8 8 8 9 9 9 |
|
2 |
0 0 0 0 1
1 2 2 2 2 2 3 3 3 3 4 4 5 5 5 6 6 6 6 7 7 7 8 8 8 9 |
|
3 |
0 1 1 2 3
|
将其分成7组:
(Ⅰ)填频率分布表,并回答零件数在区间 上的频率是多少?
上的频率是多少?
(Ⅱ)从第七组的数据中任意取两个数据,求两个数据恰好相等的概率.
频率分布表
|
分组 |
频数 |
频率 |
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
|
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com