1．例题：

例1．求下列三角函数值：(1)；　 (2)； (3)．

分析：先将不是范围内角的三角函数，转化为范围内的角的三角函数(利用诱导公式一)或先将负角转化为正角然后再用诱导公式化到范围内角的三角函数的值。

解：(1)(诱导公式一)

(诱导公式四)．

(2)(诱导公式二)(诱导公式一)

(诱导公式四)．

(3)

小结：用诱导公式可将任意角的三角函数化为锐角的三角函数，其一般步骤是：

①化负角的三角函数为正角的三角函数；

②化大于的正角的三角函数为内的三角函数；

③化内的三角函数为锐角的三角函数．

可概括为：“负化正，大化小，化到锐角为终了”(有时也直接化到锐角求值)．

例2．判断下列函数的奇偶性：

(1)；　 (2)．

解 (1)因为函数的定义域是，且，

　　　 所以是偶函数．

　 (2)因为函数的定义域是，且

　　　 ，

　　　 所以是奇函数．

说明：公式二可直接对应三角函数的奇偶性．

例3．化简．

解：①当时，

原式．

②当时，

原式．

说明：关键抓住题中的整数是表示的整数倍与公式一中的整数有区别，所以必须把分成奇数和偶数两种类型，分别加以讨论．

三角函数的诱导公式：

(1)公式一：

(2)公式二：

(3)公式三：

(3)公式四：

说明：①公式中的指使公式两边有意义的任意一个角；

②若是角度制，同样成立,如，；

③公式特点：函数名不变，符号看象限；

如果角的终边与角的终边关于轴对称，那么与的三角函数值之间有什么关系？

设角，的终边分别与单位圆交于点，，则点和点关于轴对称(如图)．又根据三角函数的定义，点的坐标是，点的坐标是．故有．

由同角三角函数关系得．

特别地，角与角的终边关于轴对称，故有

如果角的终边与角的终边关于轴对称，或是关于原点对称，那么与的三角函数值之间有什么关系？

(一)复习：

(1)利用单位圆表示任意角的正弦值和余弦值：为角的终边与单位圆的交点

则　 ，；

(2)由三角函数定义可以知道：终边相同的角的同一三角函数相等．

即有

2．问题：

除此之外还有一些角，它们的终边具有某种特殊关系，如关于坐标轴对称、关于原点对称等，那么它们的三角函数有何关系呢？

1．情境：

《高中数学精讲精练》(一)

《三点一测丛书》

(四)总结

本节课我们学习了π±α，-α，2π-α形式的诱导公式，可用口诀“函数名不变，符号看象限”来帮助记忆，正确掌握诱导公式符号是运用诱导公式解题的关键．

(三)诱导公式四、五

师：请同学们思考如何利用已学过的诱导公式推导180°-α与α的三角函数值之间的关系？

生：由诱导公式我们可以得到

sin(180°-α)=sin[180°+(-α)]=-sin(-α)=sinα；

cosα(180°-α)=cos[180°+(-α)]=-cos(-α)=-cosα；

tg(180°-α)=tg[180°+(-α)]=tg(-α)=-tgα；

ctg(180°-α)=ctg[180°+(-α)]=ctg(-α)=-ctgα．

公式四：

sin(180°-α)=sinα，cos(180°-α)=-cosα，tg(180°-α)=-tgα，ctg(180°-α)=-ctgα．

师：请大家再思考如何利用已学过的诱导公式推导360°-α与α的三角函数值之间的关系．

生：由诱导公式我们可以得到：

sin(360°-α)=sin(-α)=-sinα， cos(360°-α)=cos(-α)=cosα，

tg(360°-α)=tg(-α)=-tgα，　 ctg(360°-α)=ctg(-α)=-ctgα．

师：于是我们得到诱导公式五

sin(360°-α)=-sinα，cos(=360°-α)=cosα，

tg(360°-α)=-tgα，ctg(360°-α)=-ctgα．

公式一、二、三、四、五都叫做诱导公式．

上面这些诱导公式，可以概括如下：

k·360°+α(k∈z)，-α，180°±α，360°-α的三角函数值等于α的同名函数值，前面加上一个把α看成锐角时原函数值的符号．简化成“函数名不变，符号看象限”的口诀。请同学思考利用诱导公式求任意角的三角函数值的步骤，即如何利用诱导公式将任意角的三角函数求值问题化归成锐角三角函数求值问题？请看下面例题后总结其步骤．

例4　 求下列各三角函数值

(2)cos(-1665°)=-cos1665°=-cos(4×360°+225°)=-cos225°

师：反思例4的解题过程，请一位同学总结．

生：利用诱导公式求任意角的三角函数值，一般可按以下步骤进行：

师：运用诱导公式解题本质上是多次运用“化归”思想方法，化负角为正角，化大角为周内角，再化为锐角．

(二)诱导公式二、三

师：首先我们先介绍单位圆概念，如图2-18示，以原点为圆心，等于单位长的线段为半径作一个圆，这样的圆称为单位圆．下面我们利用单位圆和任意角三角函数的定义来推导诱导公式二、三．推导之前，请一位同学回答分别关于x轴，y轴，原点对称的两个点的坐标间的关系．

生：设点P(x、y)，它关于x轴、y轴、原点对称的点坐标分别是P1(x，-y)，P2(-x，-y)，P3(-x，-y)．

师：请同学们作出一个任意角α的终边，再作出180°+α角的终边，它们与单位圆的交点有何特征？为什么？

生：如图2-18，任意角α的终边与单位圆交于点P(x，y)．由于角180°+α的终边就是角α终边的反向延长线，角180°+α的终边与单位圆的交点P′，是与点P关于点O对称的。

师：正由于点P与点P′关于原点O中心对称，所以P′坐标是(-x，-y)，又因单位圆半径r=1，由正弦函数和余弦函数的定义可得到

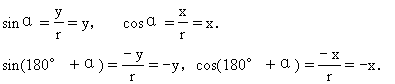
因此，sin(180°+α)=-sinα，cos(180°+α)=-cosα，请同学们思考能否由同角三角函数关系式推导出tg(180°+α)，ctg(180°+α)化简结果？

生：由同角三角函数间的基本关系式，可得到

师：因此我们可以得到诱导公式二

sin(180°+α)=-sinα，cos(180°+α)=-cosα，

tg(180°+α)=tgα，ctg(180°+α)=ctgα．

例1　 求下列各三角函数值

师：我们再来研究角α与-α的三角函数值之间的关系．请同学们作出任意角α与-α的终边，它们与单位圆的交点有何特征？为什么？

生：如图2-19，任意角α的终边与单位圆相交于P(x，y)，角-α的终边与单位圆相交于点p′，从图上可观察得到P与P′关于x轴成轴对称．

师：这位同学回答得正确！由于角α与-α是由射线从x轴的正半轴开始，按相反的方向绕原点作相同大小的旋转而成的，这两个角的终边关于x轴对称，因此，点p′的坐标为(x，-y)，由于r=1，我们得到sinα(-α)=-y，cos(-α)=x，从而sin(-α)=-sinα，(cos(-α)=cosα．如何由同角三角函数关系式推导出tg(-α)．ctg(-α)的化简结果？

生：由同角三角函数关系式可得到

师：因此我们可以得到诱导公式三

sin(-α)=-sinα，cos(-α)=cosα，

tg(-a)=-tgα，ctg(-α)=-ctgα．

例2　 求下列各三角函数值

(1)sin(-400°)=-sin(360°+40°)=-sin40°=-0.6428，

解：∵　 ctg(-α-180°)=ctg[-(180°+α)]=-ctg(180°+α)=- ctgα，

sin(-180°-α)=sin[-(180°+α)]=-sin(180°+α)=-(-sinα)=sinα．

课堂练习：P．155中练习3(1)、(3)、(6)；4．