
题目列表(包括答案和解析)
2.抛物线 在点
在点 处的切线方程是( A
)
处的切线方程是( A
)
A. B.
B. C.
C. D.
D.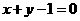
1.计算 的结果是( B
)
的结果是( B
)
A. B.
B. C.
C. D.
D.
22、(本小题满分12分)
已知函数 在
在 时有极大值6,在
时有极大值6,在 时有极小值,
时有极小值,
(1)求 的值; (2)求
的值; (2)求 在区间[-3,3]上的最大值和最小值.
在区间[-3,3]上的最大值和最小值.
解:(1) 由条件知
由条件知
 。。。。。。。。。。。。6分
。。。。。。。。。。。。6分
(2)
|
x |
-3 |
(-3,-2) |
-2 |
(-2,1) |
1 |
(1,3) |
3 |
 |
|
+ |
0 |
- |
0 |
+ |
|
 |
 |
↗ |
6 |
↘ |
 |
↗ |
 |
由上表知,在区间[-3,3]上,当 时,
时,
 时,
时, 。。。。。。
。。。。。。
|

|
版权所有:()
版权所有:()
21、(本小题满分12分)
已知点 是圆
是圆 上的动点,
上的动点,
(1)求 的取值范围;
的取值范围;
(2)若 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
解:(1)设圆的参数方程为 ,
,


(2)

20、(本小题满分12分) 已知 ,且
,且 ,求证:
,求证: 与
与 中至少有一个小于2.
中至少有一个小于2.
解:用反证法.假设 与
与 都大于或等于2,即
都大于或等于2,即 , ----------4分
, ----------4分
 ,故可化为
,故可化为 ,
,
两式相加,得 ,
----------------------------------------10分
,
----------------------------------------10分
与已知 矛盾.所以假设不成立,即原命题成立.
--------------------12分
矛盾.所以假设不成立,即原命题成立.
--------------------12分
19、(本小题满分12分)
已知集合 ,
, ,且
,且 ,
,
求实数 的取值范围.
的取值范围.
解:由条件 可知,
可知, .
.
当 时,
时, ,解得
,解得 ; ……………3分
; ……………3分
当 时,
时, 解得
解得 ;…………6分
;…………6分
综上可知,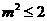 ,即
,即 . …………………8分
. …………………8分
18、(本小题满分12分)
某城市理论预测2000年到2004年人口总数与年份的关系如下表所示
|
年份200x(年) |
0 |
1 |
2 |
3 |
4 |
|
人口数 y (十万) |
5 |
7 |
8 |
11 |
19 |
(1)请画出上表数据的散点图;
(2) 请根据上表提供的数据,求最小二乘法求出 y 关于x的线性回归方程y = b x + a ;
(3)据此估计2005年该城市人口总数。
 (参考数值:0×5+1×7+2×8+3×11+4×19=132,
(参考数值:0×5+1×7+2×8+3×11+4×19=132, ,公式见卷首 )
,公式见卷首 )
|
17、(本小题满分10分) 已知直线的参数方程为 ,圆的极坐标方程为
,圆的极坐标方程为

(I)求直线的普通方程和圆的直角坐标方程;
(II)求直线被圆截得的弦长。
(I)直线的普通方程为: ;
;
圆的直角坐标方程为: ………………4分
………………4分
(II)圆心到直线的距离 ,
,
直线被圆截得的弦长 ………………10分
………………10分
16.由下列各式: ……,归
……,归
纳第 个式子应是___________
个式子应是___________ _.
_.
14、已知 ,则
,则 的值是 2
的值是 2
15极坐标方程分别为 与
与 的两个圆的圆心距为_________
的两个圆的圆心距为_________ 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com