
题目列表(包括答案和解析)
4. 直线 的倾斜角是( )
的倾斜角是( )
A. 不存在 B.  C.
C. 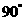 D.
D. 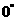
3. 函数 的定义域为 ( )
的定义域为 ( )
A.R B. C.
C. D.
D.
2. 若运行右图的程序,则输出的结果是( ).
A. 5 B. 18 C. 8 D. 13
1. 已知集合
已知集合 ,
, ,则
,则 ( )
.
( )
.
A.  B.
B.  C.
C.  D.
D. 
21、解:(1) ∴切线斜率
∴切线斜率
∴切线方程: ,即
,即
(2)
∴ 有
有
当 变化时
变化时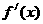 ,
, 变化如下
变化如下
 |
-1 |
(-1, ) ) |
 |
( , , ) ) |
 |
( ,1) ,1) |
1 |
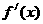 |
|
+ |
0 |
- |
0 |
+ |
|
 |
|
↗ |
|
↘ |
|
↗ |
|
 ,
, ,
, ,
,
∴当 时,
时, 有最大值
有最大值
当  时,
时, 有最小值
有最小值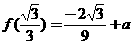
∴对任意的 ,
,

满足 ,故
,故 是“storm函数”。
是“storm函数”。
20、解:(1)根据题意,设椭圆的方程为 ,半焦距为
,半焦距为 ,则D(0,
,则D(0, ),F(
),F( ,0),
,0),
因为直线DF的斜率为 ,所以
,所以 ,①
,①
因为M(1, )在椭圆上,所以
)在椭圆上,所以 ,②
,②
又 ,③由①②③得:
,③由①②③得:
所以椭圆的标准方程为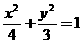
(2)设直线AB的方程为 ,代入
,代入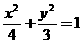 ,
,
得 ,
,
设A( ),B(
),B( ),AB为中点N(
),AB为中点N( ),
),
则 ,
, ,
,
∴ ,
, ,
,
∴AB的中垂线方程为
 ,
,
令 ,得
,得
 ,
,
又 ,∴
,∴ ,
,
∴线段AB的中垂线与 轴的交点的横坐标的取值范围是(0,
轴的交点的横坐标的取值范围是(0, )。
)。
19、解:(1)设椭圆P的方程为 ,
,
由题意得 ,
, ,
,
∴ ,
, ,
,
∴椭圆P的方程为 。
。
(2)假设存在满足题意的直线 ,易知当直线
,易知当直线 的斜率不存在时,
的斜率不存在时,
 不满足题意。
不满足题意。
故可设直线 的方程为
的方程为 ,R(
,R( ),T(
),T( )。
)。
∵ ∴
∴
 =
= 。
。
由 得
得 ,
,
由 得,
得, ,解得
,解得 。①
。①
∴ ,
, ,
,
∴ =
= ,
,
故
 =
= +
+

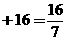 ,解得
,解得 ,②
,②
由①②解得 ,
,
∴直线 的方程为
的方程为 。
。
故存在直线 或
或 满足题意。
满足题意。
18、解:(1)切点坐标(1,-12),
∴ ∴
∴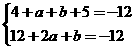 ∴
∴
∴
(2) ∴
∴ 有
有 或
或
当 变化时
变化时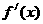 ,
, 变化如下:
变化如下:
 |
-3 |
(-3,-1) |
-1 |
(-1,1) |
1 |
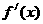 |
|
+ |
0 |
- |
|
 |
|
↗ |
|
↘ |
|
 ,
, ,
,
∴当 时有最小值
时有最小值 ; 当
; 当 时,有最大值
时,有最大值 。
。
17、解:∵ ∴
∴
∴ ∴圆心直角坐标为C
∴圆心直角坐标为C
∴所求直线的直角坐标方程为
∴极坐标方程为 。
。
13.3 14、 15、
15、 16、8
16、8
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com