
题目列表(包括答案和解析)
16.图(1)、(2)、(3)、(4)分别包含1个、5个、13个、25个第二十九届北京奥运会吉祥物“福娃迎迎”,按同样的方式构造图形,设第 个图形包含
个图形包含 个“福娃迎迎”,则
个“福娃迎迎”,则 .(答案用数字或
.(答案用数字或 的解析式表示)
的解析式表示)

15.若曲线 存在垂直于
存在垂直于 轴的切线,则实数
轴的切线,则实数 的取值范围是 .
的取值范围是 .
14. 1+x
(填>或< )
1+x
(填>或< )
13.已知 ,则
,则 .
.
(17)(本小题满分10分) 已知:

通过观察上述两等式的规律,请你写出一般性的命题,并给出的证明.






















(18)(本小题满分12分)某高校“统计初步”课程的教师随机调查了选该课的一些学生情况,具体数据如下表:
|
专业 性别 |
非统计专业 |
统计专业 |
|
男 |
13 |
10 |
|
女 |
7 |
20 |
根据表中的数据,判断选修统计专业是否与性别有关系.
( 其中
其中 为样本容量)
为样本容量)
(19)(本小题满分12分)已知函数 .
.
(1)试问该函数能否在 处取到极值?若有可能,求实数
处取到极值?若有可能,求实数 的值;否则说明理由;
的值;否则说明理由;
(2)若该函数在区间 上为增函数,求实数
上为增函数,求实数 的取值范围.
的取值范围.
(20)(本小题满分12分)已知 是复数,
是复数, ,
, 均为实数(
均为实数( 为虚数单位),且复数
为虚数单位),且复数 在复平面上对应的点在第一象限,求实数
在复平面上对应的点在第一象限,求实数 的取值范围.
的取值范围.
(21)(本小题满分12分)已知函数 若
若 时,
时, 有极值.
有极值. 在点
在点 处的切线l不过第四象限且斜率为3,又坐标原点到切线l的距离为
处的切线l不过第四象限且斜率为3,又坐标原点到切线l的距离为 .
.
(1)求 的值;
的值;
(2)求 上的最大值和最小值.
上的最大值和最小值.
 (22)(本小题满分12分)已知二次函数
(22)(本小题满分12分)已知二次函数 ,其导函数
,其导函数 的图象如图,
的图象如图,
(1)求函数 处的切线斜率;
处的切线斜率;
(2)若函数 上是单调函数,求实数
上是单调函数,求实数 的取值范围;
的取值范围;
(3)若 的图像总在函数
的图像总在函数 图象的上方,求
图象的上方,求 的取值范围.
的取值范围.
(13)若 .则
.则 __________________________.
__________________________.
(14)已知x与y之间的一组数据:
|
x |
0 |
1 |
2 |
3 |
|
y |
1 |
3 |
5 |
7 |
则y与x的线性回归方程为y=bx+a必过点__________________________.
(15)函数 在
在 处有极值10, 则a的值为______________.
处有极值10, 则a的值为______________.
(16)通过计算三角形,四边形,五边形的对角线条数,推测凸 边形
边形 的对角线条数为__________________________.
的对角线条数为__________________________.
(1)化简 ( )
( )
(A) (B)
(B) (C)
(C) (D)
(D)
(2)已知 为等比数列,
为等比数列, ,则
,则 .若
.若 为等差数列,
为等差数列, ,则
,则 的类似结论为
( )
的类似结论为
( )
(A) (B)
(B)
(C) (D)
(D)
(3)若(x2-1)+(x2+3x+2)i是纯虚数,则实数x的值是 ( )
(A) (B)
(B) (C)
(C) 或
或 (D)
(D) 或
或
(4)有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线 平面
平面 ,直线
,直线 平面
平面 ,直线
,直线 ∥平面
∥平面 ,则直线
,则直线 ∥直线
∥直线 ”的结论显然是错误的,
”的结论显然是错误的,
这是因为 ( )
(A)大前提错误 (B)小前提错误 (C)推理形式错误 (D)非以上错误
(5) ( )
( )
(A) 1 (B)  (C) -
(C) - (D) -1
(D) -1
(6)下列求导运算正确的是 ( )
(A) (B)
(B)
(C) (D)
(D)
(7)两个变量 与
与 的回归模型中,分别选择了4个不同模型,它们的相关指数
的回归模型中,分别选择了4个不同模型,它们的相关指数 如下 ,其中拟合效果最好的模型是
( )
如下 ,其中拟合效果最好的模型是
( )
(A)模型1的相关指数 为0.98 (B)模型2的相关指数
为0.98 (B)模型2的相关指数 为0.80
为0.80
(C)模型3的相关指数 为0.50 (D)模型4的相关指数
为0.50 (D)模型4的相关指数 为0.25
为0.25
(8) 设 三数成等比数列,而
三数成等比数列,而 分别为
分别为 和
和 的等差中项,则
的等差中项,则 ( )
( )
(A) (B)
(B) (C)
(C) (D)不确定
(D)不确定
(9)当x≠0时,有不等式 ( )
(A)
(B)
(C)
(D)
(10)以正弦曲线y=sinx上一点P为切点的切线为直线l,则直线l的倾斜角的范围是 ( )
(A) ∪
∪ (B)
(B)
(C) (D)
(D) ∪
∪
(11)设 小于0,则3个数:
小于0,则3个数: ,
, ,
, 的值
( )
的值
( )
(A)至多有一个不小于-2 (B)至多有一个不大于2
(C)至少有一个不大于-2 (D)至少有一个不小于2
(12)已知二次函数 的导数为
的导数为 ,
, ,对于任意实数
,对于任意实数 都有
都有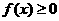 ,则
,则 的最小值为
( )
的最小值为
( )
(A) (B)
(B) (C)
(C) (D)
(D)
第Ⅱ卷(非选择题 共90分)
22. (本题满分14分)
设函数
(1)求函数 的单调区间;
的单调区间;
(2)若当 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)若关于 的方程
的方程 在区间
在区间 上恰好有两个相异的实根,
上恰好有两个相异的实根,
求实数 的取值范围;
的取值范围;
哈尔滨市第六中学2010届高二下学期期中考试
21. (本小题满分12分)
已知函数 .
.
(Ⅰ)当 时,证明函数
时,证明函数 只有一个零点;
只有一个零点;
(Ⅱ)若函数 在区间
在区间 上是减函数,求实数
上是减函数,求实数 的取值范围.
的取值范围.
20.(本小题满分12分)
已知函数
 在
在 处取得极值
处取得极值 ,其中
,其中 为常数.
为常数.
(1)求 的值;
的值;
(2)求函数 的单调区间;
的单调区间;
(3)若对任意 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com