
题目列表(包括答案和解析)
2.函数 在(-1,1)上为单调递减函数,在(1,+∞)上为单调递增函数,则
在(-1,1)上为单调递减函数,在(1,+∞)上为单调递增函数,则
A. a=1, b=1; B. a=1, b∈R; C. a=-3, b=3; D. a=-3, b∈R.
|
 的图象如图所示,下列数值排序正确的是
的图象如图所示,下列数值排序正确的是
 A.
A. ;
;
B. ;
;
|
 ;
;
D. .
.
1. 已知
已知 的定义域为R,
的定义域为R, 的导函数
的导函数 的图象如图所示,则
的图象如图所示,则
A. 在x=1处取得极小值;
在x=1处取得极小值;
B.  在x=1处取得极大值;
在x=1处取得极大值;
C.  是R上的增函数;
是R上的增函数;
D 是(-∞,1)上的减函数,(1,+∞)上的增函数.
是(-∞,1)上的减函数,(1,+∞)上的增函数.
21.(12分)已知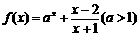 .
.
(1)证明:函数 在
在 上为增函数;
上为增函数;
(2)用反证法证明:方程 没有负数根.
没有负数根.
证明:(1) .
.
 ,
, ,
,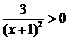 ,
, ,
,
 函数
函数 在
在 上为增函数;
上为增函数;
(2)假设存在 ,满足
,满足 ,则
,则 ,
, ,
,
∴ ,解得
,解得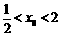 ,与假设
,与假设 矛盾.故方程
矛盾.故方程 没有负数根.
没有负数根.
20.(12分)已知点 是圆
是圆 上的动点,
上的动点,
(1)求 的取值范围;
的取值范围;
(2)若 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
解:(1)设圆的参数方程为 ,
,


(2)

19.(12分)已知过函数f(x)= 的图象上一点B(1,b)的切线的斜率为-3。
的图象上一点B(1,b)的切线的斜率为-3。
(1)求a、b的值;
(2)求A的取值范围,使不等式f(x)≤A-1993对于x∈[-1,4]恒成立;
解:(1) =
=
依题意得k= =3+2a=-3, ∴a=-3
=3+2a=-3, ∴a=-3
 ,把B(1,b)代入得b=
,把B(1,b)代入得b=
∴a=-3,b=-1
(2)令 =3x2-6x=0得x=0或x=2
=3x2-6x=0得x=0或x=2
∵f(0)=1,f(2)=23-3×22+1=-3
f(-1)=-3,f(4)=17
∴x∈[-1,4],-3≤f(x)≤17
要使f(x)≤A-1993对于x∈[-1,4]恒成立,则f(x)的最大值17≤A-1993
∴A≥2010。
18.(10分)求以椭圆 内一点P(1,-1)为中点的弦所在直线的方程。
内一点P(1,-1)为中点的弦所在直线的方程。
解:由已知条件可知所求直线的斜率 存在且不为0,故可设所求直线方程为:
存在且不为0,故可设所求直线方程为:
 ,即
,即 代入椭圆方程
代入椭圆方程 得:
得:
 ①,设所求直线与已知椭圆的交点A、B的坐标分别为
①,设所求直线与已知椭圆的交点A、B的坐标分别为 ,所以
,所以 是方程①的两个根,
是方程①的两个根,
又因为点P(1,-1)是线段AB的中点,所以有 ,
,
即 ,解得
,解得 ,所以所求直线的方程为
,所以所求直线的方程为

17.(10分)已知 ,求证:
,求证: .
.
证明:
 ,
,
 .
.
又 ,
, ,
, ,
,
 将以上三个不等式相加,得
将以上三个不等式相加,得 ,
,
 .
.

 .
.
16.直线 的极坐标方程为____________________。
的极坐标方程为____________________。
15.在复平面内,O是原点,向量 对应的复数3+
对应的复数3+ ,如果A关于实轴的对称点B,则向量
,如果A关于实轴的对称点B,则向量 对应的复数为
.
对应的复数为
.

14. ,
, ,
, ,计算
,计算 分别为
分别为 ,猜想
,猜想 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com