
题目列表(包括答案和解析)
20.(16分) 已知函数 的定义域为
的定义域为 ,且同时满足:对任意
,且同时满足:对任意 ,总有
,总有 ,
, ;
;
若 ,
, 且
且 ,则有
,则有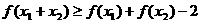 .
.
(1)求 的值;
的值;
(2)试求 的最大值;
的最大值;
(3)设数列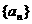 的前
的前 项和为
项和为 ,且满足
,且满足 ,
,
求证: .
.
江苏省赣榆高级中学高二数学答题卷
19.(16分) 随机抽取某厂的某种产品400件,经质检,其中有一等品252件、二等品100件、三等品40件、次品8件.已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元,而1件次品亏损2万元.设1件产品的利润(单位:万元)为 .
.
(1)求 的分布列和数学期望;
的分布列和数学期望;
(2)经技术革新后,仍有四个等级的产品,但次品率降为 ,一等品率提高为
,一等品率提高为 .如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
.如果此时要求1件产品的平均利润不小于4.73万元,则三等品率最多是多少?
18.(16分)现有甲、乙两个盒子,甲盒中装有4个白球和4个红球,乙盒中装有3个白球和若干个红球,若从乙盒中任取两个球,取到同色球的概率是 .
.
(Ⅰ)求乙盒中红球的个数;
(Ⅱ)若从甲盒中任取两个球,放入乙盒中均匀后,再从乙盒中任意取出2个球放回到甲盒中,求甲盒中白球没有增加的概率;
(Ⅲ)从甲、乙两个盒子中各任取两个球进行交换,若交换后乙盒子中的白球数和红球数相等,就说这次交换是成功的,试求当进行150次交换(都从初始状态交换)时,大约有多少次是成功的.
17.(14分) 设 ,
,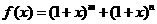 ,
,
(1)当 时,
时, ,求
,求 。
。
(2)当 时,
时, 展开式中
展开式中 的系数是20,求
的系数是20,求 的值。
的值。
(3) 展开式中
展开式中 的系数是19,当
的系数是19,当 ,
, 变化时,求
变化时,求 系数的最小值。
系数的最小值。
16.( 14分)某班有8人,现在要从中选出5人去参加一项活动,按下列要求,有多少种不同的选法?(要求计算出结果)
(1)甲乙丙三人中至少有一人入选;
(2)甲乙丙三人必入选后,五人排成一排,其中甲乙必须相邻且不与丙相邻的排法。
15.( 14 分)(1)计算 ;
;
(2)已知
 求z及
求z及 .
.
14.“渐减数”是指每个数字比其左边数字小的正整数(如 ),若把所有的五位渐减数按从小到大的顺序排列,则第
),若把所有的五位渐减数按从小到大的顺序排列,则第 个数为
▲ .
个数为
▲ .
13.若 ,且
,且 则实数
则实数 中最大的一个为__▲_____.
中最大的一个为__▲_____.
12.设 (n=2,3,4…)是
(n=2,3,4…)是 的展开式中x的一次项的系数,则
的展开式中x的一次项的系数,则 (
(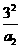 +
+ +…+
+…+ )的值是 ▲ .
)的值是 ▲ .
11.位于坐标原点的一个质点 按下列规则移动:质点每次移动一个单位,移动的方向为向上或向右,并且向上、向右移动的概率都是
按下列规则移动:质点每次移动一个单位,移动的方向为向上或向右,并且向上、向右移动的概率都是 ,质点
,质点 移动五次后位于点(
移动五次后位于点( ,
, )的概率是____▲____.
)的概率是____▲____.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com