5．不等式的解集是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　 A．　 　　　 B．　　 C．　 　　 D．

4．在对分类变量X, Y进行独立性检验时,算得=7有以下四种判断

(1) 有99﹪的把握认为X与Y有关;(2)有99﹪的把握认为X与Y无关;(3)在假设H₀:X与Y 无关的前提下有99﹪的把握认为X与Y有关;(4)在假设H₁: X与Y有关的前提下有99﹪的把握认为X与Y无关.以上4个判断正确的是　 　　　　　　　　　 (　　 )

　　　　 A． (1)、(2) 　　　　　　　 B． (1)、(3)　 　　　　　　 C． (2)、(4)　 　　　　　 D． (3)、(4)

3．若则的最小值是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　 　　 A．2　 　　　　　　　　　　　　　　 B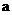．　 　　　　　　　　　　　　　 C．3　 　　　　　　　　　　　　　　 D．

2．下面几种推理是类比推理的是　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　 A．两条直线平行，同旁内角互补，如果和是两条平行直线的同旁内角，则

　　 B．由平面向量的运算性质，推测空间向量的运算性质

　　 C．某校高二级有20个班，1班有51位团员，2班有53位团员，3班有52位团员，由此可以推测各班都超过50位团员

　　 D．一切偶数都能被2整除，是偶数，所以能被2整除

1．在回归直线方程　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．当，的平均值　　　 　　　　

　　　 B．当变动一个单位时，的实际变动量

　　　 C．当变动一个单位时，的平均变动量　　　　　　　　　　　　　　　　　　　

　　　 D．当变动一个单位时，的平均变动量

22．(本题满分12分)　如图，三棱柱的底面是边长为2的等边三角形，侧面ABB₁A₁是

∠A₁AB=60°的菱形，且平面ABB₁A₁⊥ABC，M是A₁B₁上的动点.

　 (1)当M为A₁B₁的中点时，求证：BM⊥AC；

(2)试求二面角A₁－BM－C的平面角最小时三棱锥M－A₁CB的体积．

21．(本题满分12分)在一段线路中有4个自动控制的常用开关如图连接在一起。假定在2005年9月份开关能够闭合的概率都是0.7,开关能够闭合的概率都是0.8。

(1)求所在线路能正常工作的概率；

(2)计算在9月份这段线路能正常工作的概率。

20．(本题满分12分)某学校的生物实验室里有一个鱼缸，里面有6条鱼，其中4条黑色的和2条红色的，有位生物老师每周4天有课，每天上、下各一节课，每节课前从鱼缸中任取1条鱼在课上用，用后再放回鱼缸.

　 (1)求这位生物老师在一天中上、下午所捞的鱼为同色的概率；

　 (2)求这位生物老师一周中恰有两天上、下午所捞得的鱼为不同色的概率.

19．(本题满分12分)某班甲、乙、丙三名同学竞选班委，甲当选的概率为，乙当选的概率为，丙当选的概率为．

(1)求甲、乙、丙恰有一名同学当选的概率；

(2)求甲、乙、丙至多两人当选的概率．

18．(本题满分12分)排球比赛的规则是5局3胜制，A、B两队每局比赛获胜的概率分别为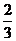和．

(1)前2局中B队以2:0领先，求最后A、B队各自获胜的概率；

(2)B队以3:2获胜的概率．