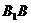19、直三棱柱中，，，D为棱 的中点

(1)求证： 平面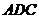

(2)求平面与平面所成的二面角的大小

18、一次数学考试中，设甲、乙、丙三人及格的概率分别是，，，且每位学生及格的事件是相互独立的，计算：

(1)三人都及格的概率；

(2)只有两人及格的概率；

(3)几个人及格的事件最容易发生。

17、从4名男生和2名女生中任选3人参加演讲比赛，设随机变量表示所选3人中女生的人数。

(1)求的分布列；

(2)求的数学期望；

(3)求“所选3人中女生人数”的概率。

16、在半径为13cm的球面上，有A、B、C 三点，AB=6cm，BC=8cm，CA=10cm，则球心到平面ABC的距离是__________

15、设随机变量-，随机变量-，若，则=_______________

14、有红、黄、篮三种颜色的小旗各3面，在每种颜色的3面小旗上分别标上号码1、2和3，现任取3面，它们的颜色与号码均不相同的概率是­_______________

13、某学校有教师200人，男学生1200人，女学生1000人，现用分层抽样的方法，从所有学生中抽取一个容量为的样本，已知从女学生中抽取的人数为80人，则=­­­­­­­­_______________

22．(本小题满分12分)

　　　　 已知函数，且函数的图象关于原点

对称，其图象在x=3处的切线方程为

　 (1)求的解析式；_{w.&w.w.k.s.5*}

　 (2)是否存在区间[m，n]，使得函数的定义域和值域均为[m，n]，且其解析式为 的解析式？若存在，求出这样一个区间[m，n]；若不存在，则说明理由.

21．(本小题满分12分)_{w.&w.w.k.s.5*}

双曲线，一焦点到其相应准线的距离为，过点A(0，-b)，B(a，0)的直线与原点的距离为

　 (1)求该双曲线的方程

　 (2)是否存在直线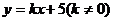与双曲线交于相异两点C，D，使得C，D两点都在以A为圆心的同一个圆上，若存在，求出直线方程；若不存在说明理由.

_{w.&w.w.k.s.5*}

20．(本小题满分12分)

　 已知斜三棱柱ABC-A₁B₁C₁，在底面ABC上的射影恰为AC的中点D，又知_{w.&w.w.k.s.5*}

　 (I)求证：AC₁⊥平面A₁BC；

　 (II)求CC₁到平面A₁AB的距离；

　 (理)(III)求二面角A-A₁B-C的大小