
题目列表(包括答案和解析)
3.把3个相同的小球放入4个不同的盒子中,每个盒子最多放2个小球,则不同方法有( )
A. 16 B. 24 C. 64 D. 81
2. 现有5双不同颜色的手套(每双手套的两只颜色相同),从中任取3只,若取出的3只手套颜色各不相同,则这样的取法有多少种?( )
A. 480 B. 360 C.120 D.80
1.代数式 的展开式的项数有( )
的展开式的项数有( )
A.12 B.13 C.60 D.360
21. 已知数列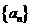 的各项均为正数,观察如下程序框图,当
的各项均为正数,观察如下程序框图,当 时,有
时,有 ,当
,当 时,有
时,有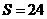 .
.
(Ⅰ)试求数列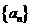 的通项公式;
的通项公式;
(Ⅱ)设数列 满足
满足 ,抽去数列
,抽去数列 中的第1项,第4项,第7项,……,第
中的第1项,第4项,第7项,……,第 项,……, 余下的项顺序不变,组成一个新数列
项,……, 余下的项顺序不变,组成一个新数列 ,求
,求 的前
的前 项和
项和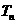 .
.
 (Ⅲ)问是否存在常数
(Ⅲ)问是否存在常数 ,使得
,使得 对任意
对任意 都成立,若存在, 求出
都成立,若存在, 求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
解:由框图 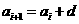 ,可知
,可知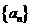 为等差数列,………………………1分
为等差数列,………………………1分
由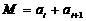
当 时,有
时,有 ①………………2分
①………………2分
当 时,有
时,有 ②………………3分
②………………3分
得 .
. ………………………4分
………………………4分
(Ⅱ)由 ,得
,得 ………………………5分
………………………5分
∵ ∴
∴ ,数列
,数列 是首项为2,公比为2的等比数列;
是首项为2,公比为2的等比数列;
(没有证明数列 为等比数列可以不扣分)
为等比数列可以不扣分)
依题意:数列 的奇数项组成首项为4,公比为8的等比数列;偶数项组成首项为8,公比为8的等比数列; ………………………6分
的奇数项组成首项为4,公比为8的等比数列;偶数项组成首项为8,公比为8的等比数列; ………………………6分
∴当 时
时
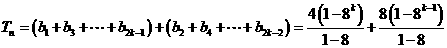
 ………8分
………8分
当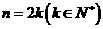 时
时

 …………………9分
…………………9分
(Ⅲ)当 时 ∵
时 ∵
∴
∵ ∴
∴ ∴
∴ ……………………11分
……………………11分
当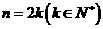 时 ∵
时 ∵
∴ ∵
∵ ∴
∴ ∴
∴
综上所得:存在常数 ,使得
,使得 对任意
对任意 都成立,
都成立, ………13分
………13分
(理)设数列 的前n项和为
的前n项和为 ,数列
,数列 满足:
满足:  ,且数列
,且数列 的前n项和为
的前n项和为 .
.
(1)求 的值;
的值;
(2)试判断:数列 是为等比数列还是等差数列?请说明理由。
是为等比数列还是等差数列?请说明理由。
(3)抽去数列 中的第1项,第4项,第7项,……,第3n-2项,……余下的项顺序不变,组成一个新数列
中的第1项,第4项,第7项,……,第3n-2项,……余下的项顺序不变,组成一个新数列 ,若
,若 的前n项和为
的前n项和为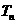 ,求证:
,求证: .
.
解:(1)由题意得:  ;………………1分
;………………1分
当n=1时,则有:  解得:
解得:  ;
;
当n=2时,则有:  ,即
,即 ,解得:
,解得:  ;
;

 ………………2分
………………2分
(2) 由 ① 得:
① 得:
 ② ………………3分
② ………………3分
② - ①得:  ,
,
即:  即:
即: ; ……………4分
; ……………4分

 ,由
,由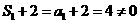 知:
知:
数列 是以4为首项,2为公比的等比数列.…………………………………6分
是以4为首项,2为公比的等比数列.…………………………………6分
(3)由(2)知:  ,即
,即 ……………………7分
……………………7分
当n≥2时,  对n=1也成立,
对n=1也成立,
即 (n
(n ………………………………………………………….…8分
………………………………………………………….…8分
 数列
数列 为
为 ,它的奇数项组成以4为首项、公比为8的等比数列;偶数项组成以8为首项、公比为8的等比数列;…………………9分
,它的奇数项组成以4为首项、公比为8的等比数列;偶数项组成以8为首项、公比为8的等比数列;…………………9分
 当n=2k-1
当n=2k-1  时,
时,


 当n=2k
当n=2k  时,
时,


 .………………13分
.………………13分
20.已知圆 :
: ,一动直线
,一动直线 过
过 与圆
与圆 相交于
相交于 、
、 两点,
两点, 是
是 中点,
中点, 与直线
与直线 :
: 相交于
相交于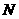 .
.
(Ⅰ)当 时,求直线
时,求直线 的方程;
的方程;
(Ⅱ)探索 是否与直线
是否与直线 的倾斜角有关,若无关,请求出其值;若有关,请说明理由.
的倾斜角有关,若无关,请求出其值;若有关,请说明理由.
解:(Ⅰ)①当直线 与x轴垂直时, 易知
与x轴垂直时, 易知 符合题意………………2分
符合题意………………2分
②当直线 与x轴不垂直时, 设直线
与x轴不垂直时, 设直线 的方程为
的方程为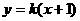 ,即
,即 ,
,
因为 ,所以
,所以 ,则由
,则由 ,得
,得 …5分
…5分
 直线
直线 :
: . 从而所求的直线
. 从而所求的直线 的方程为
的方程为 或
或 ………6分
………6分
(Ⅱ)因为 ,
,  …8分
…8分
①当 与x轴垂直时,易得
与x轴垂直时,易得 ,则
,则 ,又
,又 ,
,
 ……………………10分
……………………10分
②当 的斜率存在时,设直线
的斜率存在时,设直线 的方程为
的方程为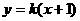 ,
,
则由 ,得
,得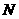 (
(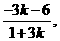
 ),则
),则 ……11分
……11分
 =
= …………………12分
…………………12分
综上, 与直线l的斜率无关,且
与直线l的斜率无关,且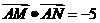 .……………13分
.……………13分
另解1:①当 与x轴垂直时,易得
与x轴垂直时,易得 ,又
,又 ,
,
则 ,
, …………………9分
…………………9分
②当 的斜率存在时,设直线
的斜率存在时,设直线 的方程为
的方程为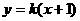 ,代入圆的方程得
,代入圆的方程得
 ,则
,则 ,
,
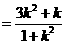 ,即
,即 (
(
 ),则
),则 …………10分
…………10分
又由 ,得
,得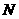 (
(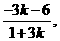
 ), 则
), 则 ………11分
………11分
 …………12分
…………12分
综上, 与直线l的斜率无关,且
与直线l的斜率无关,且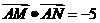 .…………13分
.…………13分
19.某厂家拟在2010年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量) 万件与年促销费用
万件与年促销费用 万元满足
万元满足 (
( 为常数),如果不搞促销活动,则该产品的年销售量是1万件. 已知2010年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).
为常数),如果不搞促销活动,则该产品的年销售量是1万件. 已知2010年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).
(1)将2010年该产品的利润y万元表示为年促销费用 万元的函数;
万元的函数;
(2)该厂家2010年的促销费用投入多少万元时,厂家的利润最大?
解:(1)由题意可知,当 时,
时,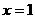 ,∴
,∴ 即
即 ,…………3分
,…………3分
∴ ,每件产品的销售价格为
,每件产品的销售价格为 元.…………4分
元.…………4分
∴2010年的利润 …………6分
…………6分

 ……8分
……8分
(2)∵ 时,
时, .…………10分
.…………10分
∴ ,当且仅当
,当且仅当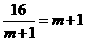 ,即
,即 时,
时, .………………12分
.………………12分
答:该厂家2010年的促销费用投入3万元时,厂家的利润最大,最大为21万元.……13分
18.如图,在三棱柱 中,每个侧面均为正方形,
中,每个侧面均为正方形, 为底边
为底边 的中点,
的中点, 为侧棱
为侧棱 的中点,
的中点,
 (Ⅰ)求证:
(Ⅰ)求证: ∥平面
∥平面 ;
;
(Ⅱ)求直线 与平面
与平面 所成角的正弦值。
所成角的正弦值。
 证明:(Ⅰ)设
证明:(Ⅰ)设 的交点为O,连接
的交点为O,连接 ,连接
,连接 .
.
因为 为
为 的中点,
的中点, 为
为 的中点,所以
的中点,所以 ∥
∥ 且
且 .
.
又 是
是 中点,则
中点,则 ∥
∥ 且
且 ,即
,即 ∥
∥ 且
且 ,
,
则四边形 为平行四边形.所以
为平行四边形.所以 ∥
∥ .
.
又 平面
平面 ,
,
 平面
平面 ,则
,则 ∥平面
∥平面 . ……………6分
. ……………6分
(Ⅱ) 过 作
作 于
于 ,因为平面
,因为平面 ,则
,则 ,连
,连 ,则
,则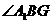 为直线
为直线 与平面
与平面 所成的线面角,………………9分
所成的线面角,………………9分
在直角三角形 中,设
中,设 ,
, ,
, ,
,
所以 ,……………11分
,……………11分
所以直线 与平面
与平面 所成角的正弦值为
所成角的正弦值为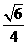 ……………12分
……………12分
17.已知向量 (
( ).向量
).向量 ,
,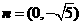 ,
,
且

 .
.
(Ⅰ) 求向量 ;
;
(Ⅱ) 若 ,
, ,求
,求 .
.
解析:(Ⅰ)∵ ,∴
,∴ ,………1分
,………1分
∵ ,∴
,∴ ,即
,即 …………① ………2分
…………① ………2分
又 ………②
………②
由①②联立方程解得, ,
, .………………5分
.………………5分
∴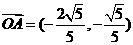 …………………………6分
…………………………6分
(Ⅱ)∵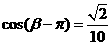 即
即 ,
, ,…………7分
,…………7分
∴ ,
, ……………8分
……………8分
又∵ ,……………9分
,……………9分
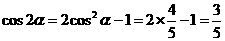 ,………………10分
,………………10分
∴ .………12分
.………12分
16. 某高中学校共有学生2000名,各年级男、女生人数如下表:
|
|
高一年级 |
高二年级 |
高三年级 |
|
女生 |
373 |
 |
 |
|
男生 |
377 |
370 |
 |
已知在全校学生中随机抽取1名,抽到高二年级女生的概率是0.19.
(I)求 的值;
的值;
(II)现用分层抽样的方法在全校抽取48名学生,问应在高三年级抽取多少名?
(III)已知 ,
,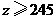 ,求高三年级中女生比男生多的概率.
,求高三年级中女生比男生多的概率.
解:(I) ……………………………… 3分()
……………………………… 3分()
(II)高三年级人数为
现用分层抽样的方法在全校抽取48名学生,应在高三年级抽取的人数为:
 (名). ………………………… 6分()
(名). ………………………… 6分()
(III)设高三年级女生比男生多的事件为A,高三年级女生男生数记为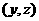
由(II)知
基本事件空间包含的基本事件有:
(245,255)、(246,254)、(247,253)、……(255,245),共11个.
事件A包含的基本事件有:
(251,249)、(252,248)、(253,247)、(254,246)、(255,245),共5个.
 高三年级中女生比男生人数多的概率是
高三年级中女生比男生人数多的概率是 ……………………………… 12分()
……………………………… 12分()
15.(文) 设函数 的定义域为D,若存在非零数
的定义域为D,若存在非零数 使得对于任意
使得对于任意 有
有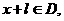 且
且 ,则称
,则称 为M上的
为M上的 高调函数。
高调函数。
现给出下列命题:
①函数 为R上的1高调函数;
为R上的1高调函数;
②函数 为R上的
为R上的 高调函数
高调函数
③如果定义域为 的函数
的函数 为
为 上
上 高调函数,那么实数
高调函数,那么实数 的取值范围是
的取值范围是
其中正确的命题是 。(写出所有正确命题的序号)[②③]
(理).对于函数f(x),若在其定义域内存在两个实数a,b(a<b),使当x∈[a,b]时,f(x)的值域也是[a,b],则称函数f(x)为“科比函数”.
(1)给出下列两个函数:① ;②
;② ,其中是“科比函数”的函数序号是
② .
,其中是“科比函数”的函数序号是
② .
(2)若函数 是“科比函数”,则实数k的取值范围是
是“科比函数”,则实数k的取值范围是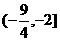 .
.
[解](1)因为 是增函数,若f(x)为“科比函数”,则f(a)=a,f(b)=b,即
是增函数,若f(x)为“科比函数”,则f(a)=a,f(b)=b,即
a+1=a,b+1=b,无解,所以 不是“科比函数”.
不是“科比函数”.
因为当x∈[0,1]时, ∈[0,1],所以
∈[0,1],所以 是“科比函数”.
是“科比函数”.
(2)因为 是增函数,若
是增函数,若 是“科比函数”,则存在实数a,b(-2≤a<b),使
是“科比函数”,则存在实数a,b(-2≤a<b),使 ,即
,即 .所以a,b为方程
.所以a,b为方程 的两个实数根,从而方程
的两个实数根,从而方程 有两个不等实根.
有两个不等实根.
令 ,则
,则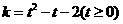 .当t=0时,k=-2;当t=
.当t=0时,k=-2;当t= 时,k=
时,k= .
.
由图可知,当 时,直线y=k与曲线
时,直线y=k与曲线 有两个不同交点,即方程
有两个不同交点,即方程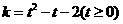 有两个不等实根,故实数k的取值范围是
有两个不等实根,故实数k的取值范围是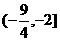 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com