23．(本小题满分14分)

如下图，过抛物线的对称轴上任一点作直线与抛物线交于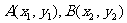两点。

　 (I)若，证明：

　 (II)在(I)条件下，若点Q是点P关于原点对称点，证明：；

　 (III)设直线AB的方程是，过A，B两点的圆C与抛物线在点A处有共同的切线，求圆C的方程。

22．(本小题满分12分)

2010年上海世博会大力倡导绿色出行，并提出在世博园区参观时可以通过植树的方式来抵消因出行产生的碳排放量，某游客计划在游园期间种植n棵树，已知每棵树是否成活互不影响，成活率都为，用表示他所种植的树中成活的棵数，的数学期望为E，方差为D。

　 (I)若n=1，求D的最大值；

　 (II)已知E=3，标准差，试求n与p的值并写出的分布列。

21．(本小题满分12分)

甲乙两奥运会主办城市之间有7条网线并联，这7条网线能通过的信息量分别为1，1，2，2，2，3，3，现从中任选三条网线，设可通过的信息量为X，当可通过的信息最，则可保证信息通畅。

　 (I)求线路信息通畅的概率；

　 (II)求线路可通过的信息量X的分布列及数学期望。

20．如果三位数的十位数既小于百位数又小于个位数，则称这样的三位数为“凹数”(如201，636，734等)，那么所有的凹数的个数为　　 　　　　。

19．双曲线的两个焦点为F₁，F₂，若P为其上一点，且|PF₁|=2|PF₂|，则双曲线离心率的取值范围为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．(1，3)　　　　　　 B．　　　　　　　　　 C．　　　　　　　 D．

18．如图，将1，2，3，4，5，6六个数字分别填入小正方形后，

按虚线折成正方体，则所得正方体相对面上两个数字的和均

相等的概率是　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．　　　　　　　　　　　　　　　　　　　　　　　　　 B．　　　　　　　　　　

　　　 C．　　　　　　　　　　　　　　　　　　　　　　　　　　 D．

17．(本小题满分14分)

　　 已知函数

　 (I)当a=1时，求函数的单调区间；

　 (II)求函数在区间[0，1]上的最小值。

第Ⅱ卷(能力附加卷，共50分)

16．(本小题满分12分)

　　 某旅游公司为3个旅游团提供甲、乙、丙、丁4条旅游线路，每个旅游团从中任选一条。

　 (I)求3个旅游团选择3条不同的旅游线路的概率；

　 (II)求恰有2条旅游线路没有被选择的概率；

　 (III)求选择甲旅游线路的旅游团数的分布列及数学期望。

15．(本小题满分8分)

　　 已知直线与椭圆(为参数)，若直线与椭圆交于A，B两点，求线段AB的长度。

14．某仪器显示屏上的每个指示灯泡均以红光或黄光或蓝光来表示不同的信号，已知一排有6个指示灯，每次显示其中的3个，且仅有2个相邻的，则一共可显示的不同信号数为

　　 　　　　　　　　　。