8、比2吨少吨是(　 　　　　)。 比2吨少是(　　　　　 )

7、一项工程，甲队独做4天完成，乙队独做6天完成。两队一起做，每天可以完成这项工程的(　 　--　 )。

6、一个数的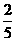是64，这个数的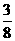是(　 　　　　　)。

5、修一段路,小明独做10天完成,小华独做8天完成.小华的工作效率是小明的( 　　　　)%

4、超市运来200千克苹果，运来的雪梨比苹果少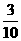，运来的雪梨比苹果少(　　　 )千克，雪梨有(　　　　 )千克。

3、一些大米，吃了，剩下的占总数的( 　-- 　)。

2、单打一份稿件，10天完成。每天完成这项工作的( -- )，8天可以完成这批零件 的(　 --　 )。

1、5月份用煤比4月份多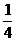，5月份用煤相当于4月份的(　 --　 ­)。

4、已知一个数的几分之几是多少，求这个数。

例如： ，表示：已知一个数的三分之一是24，求这个数。

整除与除尽

整除：

甲数除以乙数(甲、乙为自然数)，商是整数，余数为零。就说甲数能被乙数整除。

除尽：甲数除以乙数(乙数不为零)，商是有限数。就说甲数能被乙数除尽。

整除可以说是除尽，但除尽就不能说一定叫整除。

例如：1÷5＝0.2，叫除尽，但不叫整除。因为商是小数。

又如：10÷3＝3……1，既不叫整除，(因为余数不为零)也不叫除尽。

约数和倍数

当甲数能被乙数整除时，就说甲数是乙数的倍数，乙数是甲数的约数。这两个概念都是相对而存在。一个自然数，不存在是否倍数与约数。例如：“3是约数”，就是一个错误说法。只能是对3、6、9、……等数而言，是其中某个数的约数。

奇数与偶数

凡是能被2整除的数叫偶数，反之，不能被2整除的数叫奇数。

质数(素数)与合数

一个数的约数只有1和它本身的数叫做质数，也叫素数。反之，一个数的约数除了1和它本身以外，还有其他的约数，这个数就叫合数。

1是否质数

由于1的约数只有1个，所以1既不是质数，也不是合数。

公约数

几个数公有的约数，叫做公约数。

它的个数是有限的，既有最大的，也有最小的。

互质数

两个数的公约数只有1，而没有其他公约数的，这两个数就叫互质数。

质数与互质数

这两个概念没有什么联系。两个质数，不能肯定就是互质数。只有两个不相同的质数，才能肯定是互质数。另外，两个合数既可能是互质数，也可能不是互质数，但不能说两个合数一定不是互质数。

质因数

把一个合数分解成几个质数相乘的形式，这样的质数叫做质因数。

分解质因数

把一个合数分解成几个质数相同的形式，就叫做分解质因数。

公倍数

几个数公有的倍数，叫做公倍数。它的个数是无限的，只有最小的，没有最大的。

最大公约数

几个数公有的约数中，最大的一个就叫做这几个数的最大公约数。

最小公倍数

几个数公有的无限个倍数中，最小的一个，就叫做这几个数的最小公倍数。

能被2整除的判断方法

一个数能否被2整除，只要看这个数的末尾是否有0、2、4、6、8这五个数的其中一个即可。

能被5整除的判断方法

一个数能否被5整除，只要看这个数的末尾是否有0、5这两个数的其中一个即可。

能被3整除的判断方法

一个数能否被3整除，只要看这个数的各个数位上的数字和能否被3整除。

分数单位

分子为1，分母不为零的真分数，就叫这个分数的分数单位。例如： 的分数单位是 ，它有7个这样的分数单位。又如 的分数单位是 ，它有13个这样的分数单位(将带分数化成假分数)。

分数化有限小数的判断方法

一个分数能否化成有限小数，主要看分母(这里的分数一定是最简分数)是不是只有质因数“2或5”。掺杂任何其他质因数，都不能化成有限小数，反之，就一定能化成有限小数。例如： 、 、 等都能化成有限小数。 、 、 都不能化成有限小数。

分数没有基本单位

不同的分数，有不同的分数单位。没有一个共同的标准量，就没有基本单位。

分数的基本性质

一个分数的分子、分母同时乘上或除以相同的数(零除外)，分数的大小不变，这叫分数的基本性质。

分数的通分、约分

通分：把几个单位不同的分数，化成相同单位，且大小不变的分数，叫做通分。

约分：把一个分数化成同它相等的，分子、分母较小的分数，叫做约分。

百分数

表示一个数是另一个数的百分之几的数，叫做百分数。百分数又叫百分率或百分比。百分数是特殊分数。特征是分母为100，采用符号“%”(叫做百分号)来表示。分子可以是整数，也可以是小数。

百分率

两个相同量的比的比值，用百分数和的形式表示时，这个比值叫做这两个量的百分率，也叫百分比。通常的“××率”就是百分数。如“出勤率”等。

准确数与近似数(近似值)

与实际情况完全符合的数，叫做准确数。

与实际情况接近而有一定误差的数，叫做近似数(或叫近似值)。

名数与不名数

量数与计量单位名称合起来叫做名数。例如：7米、18千克、9时25分等都叫名数。

没有带单位名称的数，叫做不名数。如2、4、6、8等，都叫不名数。

单名数与复名数

只含有一个计量单位名称的名数叫做单名数。例如7米、18千克等都叫做单名数。

含有两个或者两个以上的同类计量单位名称的名数，叫做复名数。例如：2米3分米5厘米，8小时33分，8吨8千克等都叫复名数。

高级单位与低级单位

计量单位较大的叫做高级单位，计量单位较小的叫做低级单位。高、低级单位是相对的，没有单个的高、低级单位的名数。

公历年的平年、闰年

平年：把公历年份除以4(这里不是整百的公历年份)有余数时，就把这一年叫做平年，计365天。其中二月份有28天。

闰年：把公历年份除以4(这里不是整百的公历年份)余数为零时，就把这一年叫做闰年，计366天。其中二月份有29天。如果年份是整百的，则除以400，再看余数。

时刻与时间

时刻表示一天内某一个特指的时候，例如上午8时30分开会，这里的“8时30分”这是时刻。时间表示两个是期或两个时刻的间隔。例如，做作业用去30分钟，这里的“30分钟”就是时间。

比和比值

比：两个数相除，叫做两个数的比。一般地当数a除以b(b≠0)就叫做a与b的比，记作a:b。也可以用分数形式表示为 。

比值:比的前项除以后项所得的商，叫做比值。

比和比值有本质的不同。如 既可看作是比，又可看作是比值。如果化成 ，则只能表示为比值。

比的化简

把一个比化为最好简整数比，叫做比的化简。一般情况下，化简以后的比，前后两项为互质数。

比例

表示两个比相等的式子叫做比例。

正比例

两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的比值(也就是商)一定，这两种量就叫做成正比例的量，它们的关系叫做正比例关系。用字母表示： (一定)

反比例

两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的积一定，这两种量就叫做成反比例的量，它们的关系叫做反比例关系。用字母表示： (一定)

直线：没有端点，可以向两端无限延长。

射线：只有一个端点。可以向一端无限延长。

线段：有两个端点。射线和线段都是直线的一部分。

两点之间，线段最短。

垂线、垂足

两条直线相交，有一个角是直角时，就说这两条直线互相垂直。其中一条直线叫做另一条直线的垂线，其交点叫垂足。从直线外一点到直线所画的线段中，垂线最短。

角：

锐角(小于90⁰的角)、直角(等于90⁰的角)、钝角(大于90⁰而小于180⁰的角)、平角(等于180⁰的角)、周角(等于360⁰的角)

平行线

在同一平面内的两条不相交的直线，叫做平行线。

面积和地积

面积是用来表示一个物体的表面或者平面的大小。

地积就是土地的面积。

体积和容积(容量)

体积：用来表示物体所占空间的大小，叫做体积。

容积：一个容器所能容纳物体的体积，叫做容积或容量。

3、把一个数平均分成若干份，每份是多少？简称“等分除法”。

例如：24÷3，表示把24平均分成3份，每份是多少？