5.分数、百分数应用题

典型题解

★例1某车间有男工35人，女工45人，男、女工各占车间职工数的几分之几？

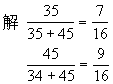
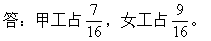
[解题关键与提示]

要求用男工数、女工数分别去比车间职工人数，车间职工人数即男、女工之和。

两天看了几页？第一天比第二天少看几页？还剩下几页没看？

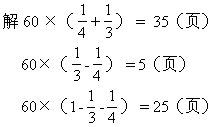
答：两天共看35页，第一天比第二天少看5页，还剩下25页没看。

[解题关键与提示]

★例3某钢厂去年产钢400万吨，今年计划比去年增产6%。今年计划增产钢多少万吨？今年计划生产多少万吨？

解　 400×6%=400×0.06=24(万吨)

400×(1+6%)=400×1.06=424(万吨)

答：今年计划增产钢24万吨，生产424万吨。

[解题关键与提示]

去年产量为“1”，增产吨数对应的百分率是400万吨的6%，生产吨数的对应百分率是(1+6%)。要求一个数的百分之几是多少，用乘法计算。

还剩下多少米？

[解题关键与提示]

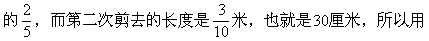
“总长-第一次剪去的长度-第二次剪去的长度”，就得到还剩下的长度。

答：全班有42人。

[解题关键与提示]

根据量率对应关系，即男生数÷男生分率=(“1”)全班人数。

这块地有多少亩？

　=150(亩)

答：这块地有150亩。

[解题关键与提示]

根据：耕的亩数÷耕的分率=一块地“1”的亩数。耕的亩数是(40+50)

有多少名？

　=21(名)

答：女生有21名。

[解题关键与提示]

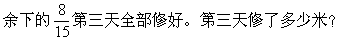
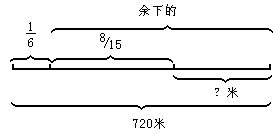
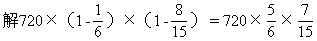
=280(米)

答：第三天修了280米。

[解题关键与提示]

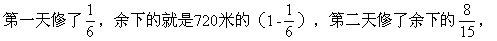
解(1)第二次运走一堆碎石的几分之几？

(2)第三次运走一堆碎石的几分之几？

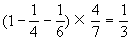
(3)这堆碎石有多少吨？

　=32(吨)

答：这堆碎石有32吨。

[解题关键与提示]

剩下的吨数÷对应的分率=碎石总数。题中三个分数的单位“ 1”不同。必须转化成都以一堆碎石为“1”的分数，然后求剩下的分率。

★★★例10有一桶油，第一次取出40%，第二次比第一次少取出10千克，桶里还剩30千克油。这桶油原来有多少千克？

解　 (30-10)÷(1-40%× 2)

＝20÷20%

=100(千克)

答：这桶油原来有100千克。

[解题关键与提示]

应该用剩下的油÷剩下的百分率=这桶油原来的重量。剩下的百分率=1-第一次取出的百分率-第二次取出的百分率。此题解答的难点是第二次取了这桶油的百分之几，这要用假定法计算了。用线段图表示题中的数量关系：

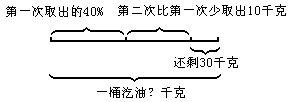
可以看到：假定第二次也取出40%。那么剩下的油就要减少10千克，是(30-10)千克了。

典型题库

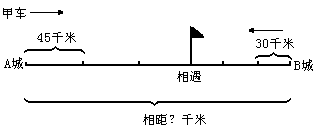
★1.一列客车和一列货车同时从两个车站相对开出，货车每小时行35千米，客车每小时行45千米，2.5小时相遇，两车站相距多少千米？

★2.两个县城相距52.5千米，甲、乙二人分别从两城同时相对而行，甲每小时行5千米，乙每小时比甲快0.5千米，几小时后相遇？

★3.甲、乙二人分别从相距110千米的两地相对而行。5小时后相遇，甲每小时行12千米，问乙每小时行多少千米？

★★4.甲、乙两站相距486千米，两列火车同时从两站相对开出，5小时相遇。第一列火车比第二列火车每小时快1.7千米，两列火车每小时的速度各是多少？

★★5.两列火车同时从相距650千米的两地相向而行，甲列火车每小时行50千米，乙列火车每小时行52千米，4小时后还差多少千米才能相遇？

★★6.大陈庄和小王庄相距90千米。小刚和小牛分别由两庄同时反向出发。2小时24分后两人相距46.6千米，如果小刚每小时行9.9千米，小牛每小时行多少千米？

★★7.学校距活动站670米，小明从学校前往活动站每分钟行80米，2分钟后，小丽从活动站往学校走，每分钟行90米，小明出发多少分钟后和小丽相遇？相遇时二人各行了多少米？

★★8.甲、乙两队合挖一条水渠，甲队从东往西挖，每天挖65米，乙队从西往东挖，每天比甲多挖2.5米。两队合挖8天后还差52米，这条水渠全长多少米？

★★9.张、李两位叔叔计划共同生产一种零件300个，二人一起生产了5小时后还差40个没完成。已知张叔叔每小时生产24个，李叔叔每小时生产多少个？

★★10.甲、乙两队合修一条长2400米的路，甲队每小时修126米，乙队每小时比甲队多修48米，求完工时两队各修路多少米？

★★11.东西两村相距64千米。甲、乙二人同时骑车从东西两地相对出发，2.5小时相遇。甲每小时行12.5千米，乙每小时比甲快多少千米？

★★★12.一列客车和一列货车分别从甲、乙两地相向而行。客车每小时行50千米，货车每小时比客车慢8千米，客车先行1小时后，货车从乙地出发，经过3小时后两车相遇。甲、乙两地相距多少千米？

★★★13.东西两城相距254千米，甲、乙两辆汽车相对开出，甲车每小时行27千米，先行2小时后，乙车开始出发，速度为每小时23千米。乙车出发几小时后两车相遇？

★★14.甲、乙两个工程队开凿一条隧道。甲队每天开凿1.5千米，乙队比甲队的2倍少0.5千米.半个月完成了任务，这条隧道有多长？

★★★15.两个车站相距360千米，两列火车相对行驶，第一列火车每小

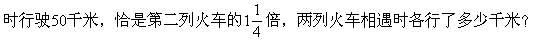
★★16.两艘客轮同时从两港相对行驶，甲轮每小时行40千米，乙轮每小时行36千米，早上8时开出，晚上11时相遇，两港口相距几千米？

★★★17.甲、乙两个工程队同时从公路的一点向两头铺沥青，甲队每天比乙队多铺20米。已知4天后两队相距880米，两队每天各铺多少米？

★★★18.小明和小华相距50步远，同时反向出发，小明每分钟走80步，小华每分钟走85步。当两人相距1700步时，出发了多少分钟？

★★★19.两辆摩托车分别从相距440千米的两地同时相向而行，因雪后路滑，5小时后才相遇。甲车比原计划每小时少行15千米，乙车比原计划每小时少行7千米。已知原计划甲车每小时的速度是乙车的1.2倍，求两车原计划每小时各行多少千米？

4.工程问题

典型题解

★例1 一项工程，由甲队做30天完成，由乙队做20天完成。(1)两队合做5天可以完成工程的几分之几？(2)两队合做10天，还剩下工程的几分之几？(3)两队合做几天完成？

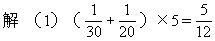
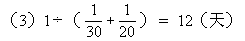
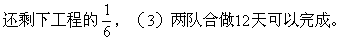
[解题关键与提示]

要解答3个问题，都离不开工作效率。甲队30天完成，总工程是“1 ”，

问题(1)要求完成的工程量，用工效×工时；问题(2)要求剩余工程量，用总工程量“1”减去已做工程量；问题(3)要求完成时间，用总工程量“ 1”÷两队工效的和。

★例2 有一件工作，小华做需3天，小芳做需4天，小梅做需5天，如果三人合做，需几天完成？

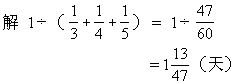
[解题关键与提示]

把这件工作的具体工作量看作“ 1”，小华单独做这件工作需3天，每天

“1”除以三人每天完成的工作量(即工效之和)，就得到三人合做需要的时间。

★例3 有一项工程，甲队单独做需要10天，甲、乙两队合做需要4天，乙单独做需要几天？

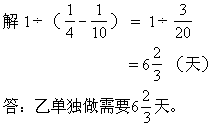
[解题关键与提示]

此题关键是要求出乙的工作效率。由于工作效率之和= 甲的工效+ 乙的工效，所以乙的工效= 工作效率之和- 甲的工效。

★★例4 一件工作，甲单独做，需要6天，乙单独做，需要8天，两人

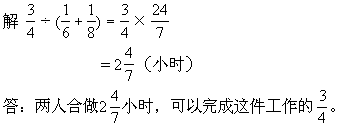
[解题关键与提示]

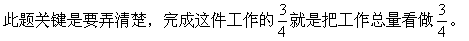
★★例5 一项工程，甲队独做60天完成，乙队独做40天完成，现先由甲队独做10天后，乙队也参加工作。还需几天完成？

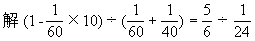
=20(天)

答：还需20天完成。

[解题关键与提示]

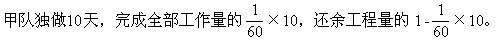
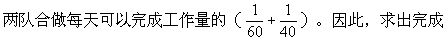
★★例6 有一项工程，甲队单独做需要10天，甲、乙两队合做需要4天。如果甲队先做3天，然后两队合做还需要几天？

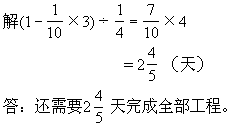
[解题关键与提示]

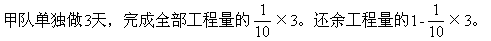
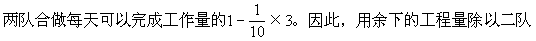
合作的效率就得到两队合做还需要的天数。

★★★例7 打字员打一部稿件，甲单独打4小时可打完，乙单独打8小时可打完，二人合打2小时后，剩下的由乙独打，还需要几小时打完？

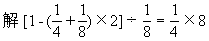
　=2(小时)

答：还需要2小时打完。

[解题关键与提示]

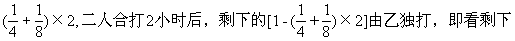
★★★例8一批货物，用一辆卡车运18次运完，用一辆大车运30次运完。现在用同样的3辆卡车和5辆大车一起运，几次可以运完？

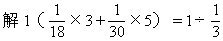
　=3(次)

答：3次可以运完。

[解题关键与提示]

以一次运的货，就得需要运的次数。典型题库

★★1.一件工程，甲独做10天完工，乙独做15天完工，二人合做几天完工？

★★2.一袋米，甲、乙、丙三人一起吃，8天吃完，甲一人24天吃完，乙一人36天吃完，问丙一人几天吃完？

★★★3.一项工程，甲独做要18天，乙独做要15天，二人合做6天后，其余的由乙独做，还要几天做完？

★★★4.一项工程，甲独做要12天完成，乙独做要18天完成，二人合做多少天可以完成这件工程的2/3？

★★★ 5.修一条路，甲单独修需16天，乙单独修需24天，如果乙先修了9天，然后甲、乙二人合修，还要几天？

★★★6.一项工程，甲独做要12天，乙独做要16天，丙独做要20天，如果甲先做了3天，丙又做了5天，其余的由乙去做，还要几天？

乙独做，又做了16天才完成，问二人独做各需要几天？

★★8.一项工程，甲独做要10天，乙独做要15天，丙独做要20天。三人合做期间，甲因病请假，工程6天完工，问甲请了几天病假？

比卡车少用2小时。如果卡车、客车分别从甲、乙两城同时相对开出，4小时后两车之间的距离占全程的几分之几？

★★10.一套家具，由一个老工人做40天完成，由一个徒工做80天完成。现由2个老工人和4个徒工同时合做，几天可以完成？

★★★11.一个水池上有两个进水管，单开甲管，10小时可把空池注满，单开乙管，15小时可把空池注满。现先开甲管，2小时后把乙管也打开，再

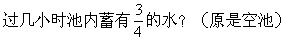
★★1.

★★2.

★★3.

★1.相遇时间= 距离之和÷(　　 )。

★2.距离之和= (　　 )。

★3.速度甲= 距离之和÷相遇时间- (　　 )；

速度乙= (　　 )。

★★4.甲、乙两人相对而行，相遇时甲行了18千米，乙行了13千米，他们原来相距(　　 )千米。

3.行程问题

典型题解

★例1 两个县城相距22千米，甲、乙二人同时从两城出发，相对而行，甲每小时行6千米，乙每小时行5千米，几小时后相遇？

解 22÷(6+5)=2(小时)

答：2小时后相遇。

[解题关键与提示]

此题可用两种方法解，(1)先求出二人每小时速度之和，减去甲每小时的速度，就等于乙每小时的速度。(2)从两城距离中减去甲2小时所行距离，就等于乙2小时所行距离，求每小时行多少干米再除以2即可。

★例2 甲、乙二人同时从两个县城相对而行，甲每小时行6千米，乙每小时行5千米，2小时后相遇，两个县城相距多远？

解 (6+5)×2=22(千米)

答：两个县城相距22千米。

[解题关键与提示]

求两个县城相距多远实际上是求甲、乙二人的距离之和，距离之和= 速度之和×相遇时间。

★例3 两个县城相距22千米，甲、乙二人同时从两城出发，相对而行，2小时后相遇，甲每小时行6千米，乙每小时行多少千米？

解　 方法(1)：22÷2-6=5(千米)

方法(2)：(22-6×2)÷2=5(千米)

答：乙每小时行5千米。

[解题关键与提示]

题中的22千米是两城的距离，是甲、乙二人一共所行的路程，实际上是二人所行的“距离之和”，而甲、乙二人共行(6+5)千米是行进时“速度之和”。求“相遇时间”就是看“距离之和”里包含了几个“速度之和”，就是几小时相遇。

★★例4 甲、乙二人同时从A、B两个县城相对而行，甲每小时行6千米，乙每小时行5千米，2小时后二人还相距4千米。两个县城相距多远？

解 (6+5)×2+4=26(千米)

答：两上县城相距26千米。

[解题关键与提示]

全程分成了三段：甲走的、乙走的、未走的，三段路程加起来，即得两城间的距离。因此，可先求出二人1小时共走的路程即速度和，再乘以二人行走的时间，这样就成为已走的和未走的两个部分相加了。如下图所示。

★★例5 一辆汽车和一辆自行车同时从甲、乙两地相向出发，4小时后两车在途中相遇，甲、乙两地相距240千米，汽车每小时行45千米。自行车每小时行多少千米？(用方程、算术两种方法解)

解　 方法(1)：设自行车每小时行x千米。

4x+ 45×4=240

4x=240-180

4x=60

　x=15

方法(2)：(240-45×4)÷4=15(千米)

答：自行车每小时行15千米。

[解题关键与提示]

两车已相遇，全程分成汽车走的与自行车走的两段，两段总长240千米，用方程解较方便。用算术解，可以这样想：全程-汽车走的路程=自行车走的路程，再除以自行车走的时间，即得速度。

★★例6 东西两地相距60千米，甲骑自行车，乙步行，同时从两地出发，相对而行，3小时后相遇。已知甲每小时的速度比乙快10千米，二人每小时的速度各是多少千米？

解　 甲：(60÷3+10)÷2=15(千米)

乙： 15-10=5(千米)

答：甲的速度是每小时15千米，乙的速度是每小时5千米。

[解题关键与提示]

甲每小时比乙快10千米，为二人“速度之差”，60÷3= 20(千米)为二人每小时的“速度之和”，因此，求二人每小时的速度可用“和差问题”的方法解答。

★★例7 两个车间要组装7200台电视机，第一车间每天组装250台，第二车间5天的组装量第一车间4天就能完成。现在两个车间同时开工，几天后能完成任务？完成任务时，两车间各组装了多少台？

解　 7200÷(250+250×4÷5)

=7200÷(250+200)

=7200÷450

=16(天)

第一车间：250×16=4000(台)

第二车间： 7200-4000=3200(台)

答：16天后能完成任务。完成任务时，第一车间组装了4000台，第二车间组装了3200台。

[解题关键与提示]

解此题的关键是要求出第二车间每天组装的台数。由“第二车间5天的组装量第一车间4天就能完成”可知250×4=1000(台)既是第一车间4天的工作量，也是第二车间5天的工作量。因此，再用1000÷5就可求出第二车间每天组装的台数。

★★★例8 体育场的环形跑道长400米，小刚和小华在跑道的同一起跑线上，同时向相反方向起跑，小刚每分钟跑152米，小华每分钟跑148米。几分钟后他们第3次相遇？

解　 设x分钟后他们第三次相遇

152x+148x=400×3

　300x=1200

x=4

答：4分钟后他们第3次相遇。

[解题关键与提示]

两人在环形道上跑步，开始“反向”，后来会转化成“相向”，所以实际上就是相向相遇问题。相遇时两人正好走完一圈。全长400米，所以第3次相遇时两人共跑了(400×3)米。因此可以按照“甲程+乙程=全程”列方程解，也可用算术方法解。

即：(1)400×3÷(152+148)= 4(分)

(2)400÷(152+148)×3= 4(分)

★★★例9 A港和B港相距662千米，上午9点一艘“寒山”号快艇从甲港开往乙港，中午12点另一艘“天远”号快艇从乙港开往甲港，到16点两艇相遇，“寒山”号每小时行54千米，“天远”号的速度比“寒山”号快多少千米？(用两种方法解)

解“寒山”号比“天远”号快艇先开时间：

12-9=3(小时)

从“天远”号开出到与“寒山”号相遇的时间：

16-12=4(小时)

方法(1)：“天远”号比“寒山”号快的千米数：

(662-54×3)÷4-54-54=500÷4-54-54

=125-54-54

=17(千米)

方法(2)：设“天远”号每小时比“寒山”号快x千米。以下略。

[解题关键与提示]

此题中的时间是用“时刻”替代的，只要把时刻转换成时间就简单了。换算的方法是：结束时间-开始时间= 经过时间。

★★★例10 甲骑摩托车，乙骑自行车，同时从相距126千米的A、B两城出发、相向而行。3小时后，在离两城中点处24千米的地方，甲、乙二人相遇。求甲、乙二人的速度各是多少？

解　 甲的速度：(126÷2+24)÷3=29 (千米/小时)

乙的速度：(126÷2-24)÷3= 13(千米/小时)

答：甲骑摩托车的速度是每小时29千米，乙骑自行车的速度是每小时13千米。

[解题关键与提示]

此题可用线段图表示：

如上图，中点处就是A、B两城正中间的地方，所以由中点处到A城和B城之间的距离都是(126÷2)千米。甲骑摩托车比乙骑自行车速度快，所以同样行3小时，行驶的路程比乙多，要在离中点24千米处相遇，因此，甲走的路程是(126÷2+24)千米；乙走的路程是(126÷2-24)千米。

典型题库

2.求平均数

典型题解

★例1 一个学习小组在一次数学测验中，小红得100分，小明得98分，小兰得96分，小平得90分，平均每人多少分？

解 (100+98+96+90)÷4=96(分)

答：平均每人96分。

[解题关键与提示]

先求出总成绩和总人数，然后求出平均数。

★例2 一辆汽车前2小时每小时行42千米，后3小时每小时行40千米，平均每小时行多少千米？

解　 (42+40)÷(2+3)

＝82÷5

=16.4(千米)

答：平均每小时行16.4千米。

[解题关键与提示]

先求出行的总路程和总时间，然后求出平均数。

★例3 某校少先队组织了4个采树种小组，采摘树种支援大西北的绿化。第一天采到15千克，第二天采到20千克，第三天采到19千克。(1)平均每天采到树种多少千克？(2)平均每组采到树种多少千克？(3)平均每组每天采到树种多少千克？

解　 (1)(15+20+19)÷3=18(千克)

(2)(15+20+19)÷4=13.5(千克)

(3)(15+20+19)÷3÷4=4.5(千克)

答：平均每天采到18干克树种，平均每组采到13.5千克树种，平均每组每天采到4.5千克树种。

[解题关键与提示]

平均的总数是共采到的树种数，始终不变；按什么“单位”平均，三个问题的要求各不相同：问题(1)要求按“天数”平均；问题(2)要求按“组数”平均；问题(3)要求按“每组每天”平均。

★例4 学校食堂第一周烧煤308千克，第二周烧煤313千克，第三周烧煤288千克。若每周按6天计算，这三周内平均每天烧煤多少千克？

解　 (308+313+288)÷(6×3)

＝909÷18

＝50.5(千克)

答：这三周内平均每天烧煤50.5千克。

[解题关键与提示]

此题先求出三周烧煤总数及烧煤天数，然后再求出平均每天烧煤多少千克。

★★例5 少先队五一中队，一次数学测验的结果是：第一小队12人，每人平均95分，第二小队12人，每人平均96分，第三小队13人，每人平均97分，第四小队12人，每人平均90分，这个中队的平均分是多少？(保留一位小数)

解　 (95×12+96×12+97×13+90×12) ÷(12+12+13+12)

＝4633÷49

＝94.6(分)

答：这个中队的平均分是94.6分。

[解题关键与提示]

先求出每个小队的总成绩，再求四个小队的总成绩及总人数，最后求平均分。

★★例6 解放军某团一连野营拉练，第一天走了32.5千米，第二天走了34.5千米，第三天比前两天的总和的一半多1.5千米，平均每天走多少千米？

解　 [ 32.5+34.5+(32.5+34.5)÷2+1.5]÷3

= [67+35]÷3

= 34(千米)

答：平均每天走34千米。

[解题关键与提示]

此题的关键是求第三天走了多少千米。“第三天比前两天的总和的一半多1.5千米”，因此前两天的总和除以2再加上1.5即(32.5+34.5)÷2+1.5=35即为第三天走的千米数。

★★★例7 某车间三个小组制作一种同样的机器零件，甲组5人做了1000个，乙组6人做的与甲组数量相等，丙组7人做的比甲、乙两组的总和还多50个，平均每人制作多少个？

解　 (1000×2+1000×2+50)÷(5+6+7)

=4050÷18

=225(个)

答：平均每人制作225个。

[解题关键与提示]

此题与例6已知条件差不多，不同的是总份数没直接给，把甲、乙、丙三组的人数加起来就是总份数。

★★★例8 有五筐苹果，第一至第四筐每筐平均有苹果181个，如果加上第五筐则平均为169个，第五筐有苹果多少个？

解　 169×5-181×4

=845- 724

=121(个)

答：第五筐有苹果121个。

[解题关键与提示]

此题根据四筐的平均数181个，可求出四筐的总数是181×4= 724(个)。又根据五筐的平均数169个，可求出五筐的总数是169×5=845个，最后再用五筐的总数减去四筐的总数就是第五筐的数量。典型题库

★1.李师傅上午工作了3小时，共加工零件246个，下午工作了4小时，共加工零件342个。李师傅这一天平均每小时加工多少个零件？

★2.自行车修理部在四月份上半月修自行车165辆，下半月修自行车195辆，四月份平均每天修多少辆？

★★3.一辆汽车给公社运化肥，上午运5次，共运30.7吨，下午运4次，比上午少运6.5吨，平均每次运化肥多少吨？

★★4.某书店一月份出售书1235本，二月份出售1009本，三月份出售1340本，四月份比三月份少出售208本，五月份至年终书的出售量比前4个月的3.5倍少198本。这年平均每月出售多少本书？

★★5.前进化肥厂去年上半年平均每月生产化肥9800吨，下半年平均每月生产化肥18700吨，今年计划比去年增产15000吨，今年计划平均每月生产化肥多少吨？

★★6.一列火车前5小时行驶了260千米，后7小时比前5小时每小时平均多行驶9千米，这列火车平均每小时行驶多少千米？

★★7.某农场35人用一周时间锄一块地，前3天共锄地70.3亩，后4天共锄地120.8亩，平均每人每天锄地多少亩？

★★8.一艘轮船从甲港驶往乙港，因顺水行驶10小时到达，从乙港返回甲港时逆水，比去时多行了5小时。甲、乙两港之间相距250千米。求这艘轮船来回的平均速度？

★★★9.李明同学数学、语文、外语考试的平均分是97分，数学、语文的平均分是96分，他的外语考了多少分？

★★10.某化肥厂四月份生产化肥4006吨，五月份生产化肥5000吨。如果要使第二季度平均月产量达到4800吨，六月份至少要生产多少吨化肥？

★★★11.有两块麦地，第一块3亩，第二块5亩，两块地平均亩产麦子370千克。第一块平均亩产320千克，第二块平均亩产多少千克？

★★★12.某校五年级一班一次数学考试，第一组9人，平均分数是90分，第二组10人，平均分数是89.5分，第三组10人，平均分数是92.2分，第四组9人，共考了774分。这个班同学的总平均分是多少分

★★1.126与72的差除以9，商是多少？

★★3.一个数的1.4倍与3的和是10，求这个数。

★★5.一个数的1.5倍正好是5.8与1.9的差，求这个数。

★★7.2.8与6的积，减去1.75除以7的商，差是多少？

★★★9.一个数的4倍与40的和正好是120，求这个数。(用方程解)

★★★12.比一个数的45%少3.5的数是14.5，求这个数。(用方程解)

★★★16.一个数的75%减去4.5与3的积等于0，求这个数。

★★★17.25增加40%后再减少20%，结果是多少？

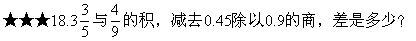
　看图计算

★例5 下图中平行四边形的面积是12平方厘米，求画斜线的三角形的面积。

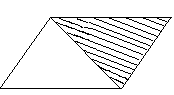
解 12÷2＝6(平方厘米)

[解题关键与提示]

三角形的面积等于和它等底等高的平行四边形的面积的一半。

★例6　 下图中哪个三角形的面积跟画斜线的三角形的面积相等？它的面积是多少？你还能画出跟画斜线的三角形面积相等的三角形吗？

解　 三角形ABD与三角形CBD的面积都跟画斜线的三角形的面积相等。

3×2÷2＝3(平方厘米)

★★例7 计算下面图形阴影部分的面积。(单位：厘米)

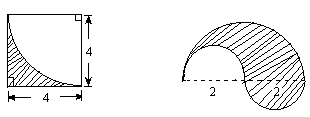
解　 4×4－3.14×4×4÷4　　　 2×2×3.14÷2

＝16－12.56＝4×3.14÷2

＝3.44(平方厘米)　　　　　 ＝6.28(平方厘米)

[解题关键与提示]

的面积。

(2)阴影部分的面积正好是半径是2厘米的圆面积的一半。

★★例8　 下图中圆的周长是18.84厘米，求阴影部分的面积。

解　 18.84÷3.14÷2＝3(厘米)

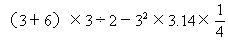
＝13.5－7.065

＝6.435(平方厘米)

[解题关键与提示]

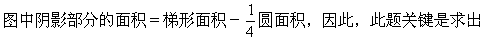
圆的半径(也是梯形的上底)。

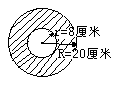
★★例9　 下图是一个圆环，R＝2厘米，r＝1厘米，求出它的面积。

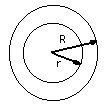
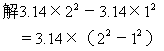
＝3.14×3

＝9.42(平方厘米)

[解题关键与提示]

圆环面积＝大圆面积－小圆面积。

★★★例10求阴影部分的面积。(单位：厘米)

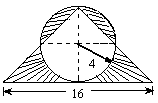
解　 (16÷2)×4÷2×2＝32(平方厘米)

[解题关键与提示]

通过旋转将阴影部分转化为：

只需求出底是(16÷2)，高是4的2个三角形面积即可。

典型题库

求下面各图形阴影部分的面积。

★★1.

★★2.

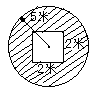
★★3.

★★4.

★★5.

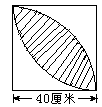
★★6.

★★7.

★★8.

★★9.

应用题

一般应用题

典型题解

★例1 小红在期中考试中，语文得了81分，政治比语文多5分，数学比政治又多6分，数学得多少分？

解 81+5+6＝92(分)

答：数学得92分。

[解题关键与提示]

弄清楚政治与语文、数学与政治的关系，一步步求出所求问题。

★例2 某煤厂第一批运来煤900吨，第二批运来煤球500吨，第三批运到的是木炭，已知木炭的数量比煤和煤球的总数少400吨，煤厂运来木炭多少吨？

解 900+500-400＝1000(吨)

答：煤厂运来木炭1000吨。

[解题关键与提示]

题中告诉我们木炭的数量比煤和煤球的总数少400吨，因此首先要求出煤和煤球的总数，然后再从煤和煤球的总数中减去木炭比煤和煤球的总数少的400吨，剩下的就是运来木炭的吨数。

★例3 某农机厂计划生产800台拖拉机。平均每天生产44台，生产了10天，余下的任务要求8天完成，平均每天要生产多少台？

解　 (800-44×10)÷8

＝360÷8＝45(台)

答：平均每天要生产45台。

[解题关键与提示]

要求余下的任务8天完成，平均每天要生产多少台，首先要知道余下的数量，从“计划生产800台拖拉机。平均每天生产44台，生产了10天”可以求出余下的数量是800-44×10＝360台，再用360÷8＝45(台)即是余下的任务8天完成，平均每天要生产的台数。

★例4 一个车间有25排机器，每排有5台，每台用3个人操作，这个车间一共有多少工人？

解　 3×5×25＝375(个)

答：这个车间一共有375个工人。

[解题关键与提示]

这类连乘应用题一定要注意被乘数的位置，列式时注意每一步算式表示的意思，如“3×5”表示每台用3个人操作，每排5台用多少个人操作，如列成“5×3”，意思就错了。

★例5　 一个修路队修路，每天修4千米，需要10天才能完工，后来改进了技术，只要8天就可修完。改进技术后，每天修路多少千米？

解(4×10)÷8＝5(千米)

答：改进技术后，每天修5千米。

[解题关键与提示]

知道改进技术后8天就可修完，要想求每天修路多少千米，还必须知道这条路一共有多长，从“每天修4千米，需要10天才能完工”可以求出这条路的全长，再用全长除以修的天数，就可得出每天修路多少千米？

★★例6 学校买10个篮球和8个小足球，共付出300元。每个小足球价格15元，每个篮球价格多少元？

解　 (300－15×8)÷10

＝180÷10

＝18(元)

答：每个篮球价格18元。

[解题关键与提示]

此题的关键是要求出“买的小足球共多少元？”“买的篮球共多少元？”这两个问题解决了，每个篮球的价格就可以计算了。

★★例7 服装厂原来做一套童装用布2.4米，改进剪裁方法后，每套节省用布0.2米，原来做264套童装的布，现在可以做多少套？

解　 2.4×264÷(2.4-0.2)

＝633.6+2.2

＝2880(套)

答：原来做264套童装的布，现在可以做2880套。

[解题关键与提示]

要想求“现在可以做多少套？”关键是要求出“现在有多少米布”及“现在每套用布多少米。”

★★例8 某工人每月工资600元，十二月份发工资后，他将工资的一半存入银行，其余的在食堂吃饭支出200元，买奶粉3袋，每袋6.80元；年底领到超额奖450元，他现在有现金多少元？

解　 600÷2-200-6.8×3+450

＝300-200-20.4+450

＝529.6(元)

答：他现在有现金529.6元。

[解题关键与提示]

注意此类题中“支出”要从总数中减去，“领到”要加上。

★★★例9 某生产队积肥，第一次25人，平均每人积肥600千克；第二次15人，平均每人比第一次多积200千克，若每亩地平均施肥500千克，这些肥料能供几亩地使用？

解 ［600×25+(600+200)×15］÷500

＝［15000+12000］÷500

＝27000÷500＝54(亩)

答：能供54亩地使用。

[解题关键与提示]

此题关键是要求出两次共积肥多少千克，在求第一次、第二次各积肥多少千克时注意被乘数的位置。

★★★例10 甲、乙两地相距400千米。一辆汽车从甲地开往乙地，以每小时45千米的速度行驶了6小时后，要求汽车在2小时内到达乙地，那么汽车平均每小时至少要比原速度加快多少千米？

解 (400-45×6)÷2-45＝130÷2-45＝20(千米)

答：汽车平均每小时至少要比原速度加快20千米。

[解题关键与提示]

解答此题的关键是要求出汽车在2小时内需要走过的路程，已知甲、乙两地相距400千米，又知汽车以每小时45千米的速度行驶了6小时，因此可求出汽车在2小时内到达乙地需走过的路程是400-45×6＝130(千米)，另外，求出汽车在2小时内到达乙地的速度后，还要注意减去原来的速度，因为最后要求的是汽车平均每小时至少要比原速度加快多少千米。

★★★例11　 某运输队有一项运送720吨货物的任务，每天运45吨，运了四天后，因特殊情况，余下的货物要在9天内运完，每天要多运几吨？(先分步列式后综合)

解(1)四天运了多少吨？

45×4＝180(吨)

(2)还剩下多少吨？

720-180＝540(吨)

(3)剩余货物要9天运完，每天平均运多少吨？

540÷9＝60(吨)

(4)现在每天要多运几吨？

60-45＝15(吨)

综合算式：

(720-45×4)÷9－45＝540÷9-45＝15(吨)

答：每天要多运15吨。

[解题关键与提示]

此题已知条件较多，分析时可从问题入手，其思考过程如下：

典型题库

★1.少先队员捡废铁，一月份捡了898千克，二月份捡了978千克，三月份比二月份少捡15千克。问三月份捡废铁多少千克？

★★2.某生产队有两块棉田，一块是14亩，每亩收皮棉91千克，另一块是17亩，每亩收皮棉103.5千克，这两块田共产皮棉多少千克。

★★3.红星农场要收割540公亩小麦。原计划6天收割完，实际每天比原计划多收割18公亩。实际用多少天收割完？

★★4.益生农机厂计划生产800台拖拉机。平均每天生产44台，生产了10天，余下的任务要求8天完成，平均每天要生产多少台？

★★5.买2.5千克的桔子比买1.5千克的苹果多花了4.3元，已知每千克苹果1.8元，每千克桔子多少元？

★★6.一盒同样规格的铁钉共重600克，取出250个铁钉后，剩下的重525克。原来这盒铁钉有多少个？

★★7.一个小商店运进15袋红枣，每袋24千克，若每500克售价为1.8元，一共可以卖多少元？

★★8.小红在假期里读一本小说，原计划每天早晨读10页，中午读8页，用15天读完，实际她每天晚上又读9页，这样她提前几天读完？

★★★9.某机械厂用5个大铁块、3个小铁块，浇铸了一个重555千克的机件；又用同样的大铁块7个、小铁块3个，浇铸了一个重705千克的机件。问大、小两种铁块每个各重多少千克？

★★10.某工厂举办业余文化学习班，参加第一期的92人，第二期比第一期多45人，第三期是第一期的2倍。问三期共有多少人参加了学习班？

★★★11.某工厂徒工平均每人每小时能加工零件4个，师傅每人每小时平均能加工零件7个。一个车间共有师傅、徒工35人，在一小时内共加工零件155个。问师傅、徒工各几人？

★★12.园林工人要给600棵果树剪枝。原计划12天完成，实际比原计划每天剪的棵数的1.5倍还多5棵，实际比原计划提前几天完成任务？

★13.修一条路，已经修好700米，比没修的4倍还多20米。这条路全长多少米？

★★★14.宏光造纸厂去年造纸4.8万吨，今年前8个月的产量就等于去年全年的产量。照这样计算，今年的平均月产量比去年增产多少万吨？

★★15.某校六年级三个班共有60本科技书。如果二班向一班要来2本，再送给三班5本，则三个班的本数正好相等。三个班原来各有多少本？

★★16.货场有一批货物用5辆载重量是4吨的卡车和4辆载重量是8吨的卡车各运了10次，还剩下80吨。这批货物有多少吨？

★★17.某生产队计划挖一条长2400米的水渠，已经挖了5天，平均每天挖60米，剩下的用25天挖完，平均每天应挖多少米？(用方程解)

★★18.某建筑工地要运64吨水泥。先用6辆载重4吨的汽车运一次，剩下的改用载重5吨的汽车运，一次运完需要多少辆？(用方程解)

★★★19.停车场上停着大客车和小轿车，停车场上的大客车数比小轿车的3倍多15辆，比小轿车的4倍少35辆，两种车各有多少辆？

典型应用题

1.归一问题和倍比问题

典型题解

★例1 某人步行，3小时行15千米，7小时行多少千米？

解 15÷3×7＝35(千米)

答：7小时行35千米。

[解题关键与提示]

先求出一个单位量即每小时行多少千米，然后再求出几个单位的总量即7小时行多少千米。这类解法叫“归一法”。

★例2　 5个人2小时植树20棵，6个人3小时植树多少棵？

解　 20÷5÷2×6×3

＝2×6×3

＝36(棵)

答：6个人3小时植树36棵。

[解题关键与提示]

要求6个人3小时植树多少棵，必须先求出5个人1小时植的棵数，再求出1个人1小时所植的棵数。

★例3 一辆卡车3次运货20吨。照这样算，9次可运货多少吨？

解 20×(9÷3)＝60(吨)

答：9次可运货60吨。

[解题关键与提示]

9次是3次的3倍，每次运货量不变，运的货一定是20吨的3倍。这类解法叫“倍比法”。

★★例4 某厂运来一批煤，计划每天用5吨，40天用完，如果改进锅炉，每天节约1吨，这批煤可以用多少天？

解　 5×40÷(5-1)

＝200÷4

＝50(天)

答：这批煤可以用50天。

[解题关键与提示]

从“计划每天用5吨，40天用完”中，可求出煤的总吨数，把总吨数除以改进锅炉后每天用煤量，可得用煤天数。

★★例5 某车间用4台车床5小时生产零件600个，照这样算，增加3台同样的车床后，(1)8小时可以生产多少个零件？(2)如果要生产6300个零件几小时可完成？

解　 600÷5+4÷(4+3)×8

＝30×7×8

＝1680(个)

6300÷［600÷5÷4×(4+3)］

＝6300÷［30×7］

＝30(小时)

答：(1)8小时可以生产1680个零件。(2)如果要生产6300个零件30小时可以完成。

[解题关键与提示]

此题要求的两个问题都需知1台1小时生产的零件数，因条件中有小时和台数两个量，需用“两次归一”，即先求出4台1小时生产多少，再求1台1小时生产多少。

★★例6　 8个工人3小时制作机器零件360个，如果人数缩小了2倍，时间增加了5小时，可制作机器零件多少个？

解　 36O÷8÷3×(8÷2)×(3+ 5)

＝15×4×8

= 480(个)

答：可制作机器零件480个。

[解题关键与提示]

此题中人数缩小了2倍指现在的人数是8÷2=4(人)；时间增加了5小时指现在的时间是3+5=8(小时)。

★★★例7　 12人25天挖了一个长60米、宽2米、高2.8米的防空洞，照这样的速度计算，30人用20天挖防空洞可以挖土多少立方米？

解　 60×2×2.8÷12÷25×30×20

＝336÷12÷25×30×20

=1.12×30×20

= 672(立方米)

答：30人用20天挖防空洞可以挖土672立方米。

[解题关键与提示]

此题和例6不同在12人25天挖的立方米数未直接给，因此第一步先要通过“长60米、宽2米、高2.8米”求出挖的总数为 60×2×2.8=336(立方米)，然后方法同例6。

★★★例8 某工地的一项工程，原计划由30人工作，每天工作8小时，45天完工。为了提前完工，实际由54人工作，每天工作10小时，可以提前几天完工？

解　 45-8×30×45÷(10×54)

＝45-10800÷540

＝45-20

＝25(天)

答：可以提前25天完工。

[解题关键与提示]

此题的关键是要先求出工程的总工时数 8×30×45= 10800(小时)及实际每天做工时数10×54=540(小时)。

典型题库

★1. 一台拖拉机5小时耕地75亩，照这样计算，14小时可以耕地多少亩？

★2. 三年级少先队员3天栽树苗2700棵，按照这样的速度，栽8100棵需要多少天？

★3. 某工人4小时做机器零件27个，8小时做多少个？

★★4. 5台机器8小时共生产钉子5000千克，7台这样的机器24小时共可生产钉子多少千克？

★★5.一部6000字的稿件，3个打字员4小时打完，如果要2小时打完，需要几个人？

★★★6.中山公园有一块长10.4米，宽5米的花坛，共种200棵花，南湖公园有长40.95米、宽5米的一个花坛，也准备按中山公园花坛的种花疏密程度栽种，问能栽多少棵花？

★★★7.工程兵某连要修一条公路，3天修路6000米，剩下没修的路比修好的2.5倍少304米，求还需多少天可修完？(保留两位小数)

★★8.养路队维修铁路，25人5天维修6250米，如果按此生产率计算，如果再增加5个人维修15000米铁路，需用多少天？

★★★9.某连队要修一条长520米的水渠，10天修了320米，剩下的要求4天完成。剩下的每天要比前10天每天多挖多少米？

★★10.20个人5小时摘棉花500千克，摘棉机每小时可摘250千克，100个人8小时所摘的棉花，如果用摘棉机去摘，几小时可摘完？

★★11.3部推土机45分钟推平1350公亩土地，两部这样的推土机，要推平长300米，宽120米的土地，需要多少时间？

★★12.某农场养马16匹，养牛46头，10天吃草6500千克。每头牛每天吃草11千克，每匹马每天吃草多少千克？

★★13.服装厂原计划16人在5天里做160套学生校服，刚要生产时又增加了任务，在工作效率不变的情况下，需要20人做9天才能完成。增加的任务是多少套？

★★★14.学校买来一批粉笔，原计划18个班可用60天，实际用45天后，有3个班外出了，剩下的粉笔够在校班级用多少天？

★★★15.12人5天平整土地360公亩。如果每人每天工作效率提高25%，30人平整2700公亩土地需要几天完成？

★1.x+78＝172

★2.576－x＝324

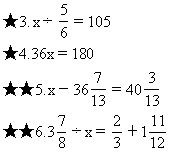
★★7.0.2x+4.6＝38.4

★★8.12.5%x＝14.4

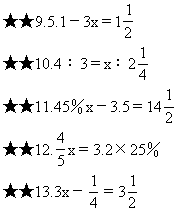
★★14.256－8x＝64

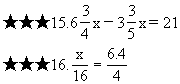
★1.7586+29070÷285

★2.8975-32×238

★3.43.6×1.5-21.43

★★4.750.4+235.2÷98×8.5

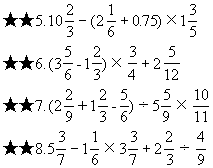
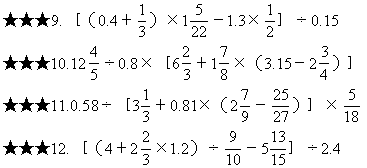
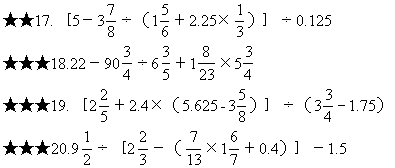
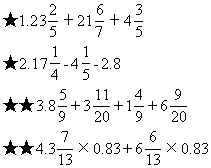
★7.17.28+9.9

★★8.0.36×8.4+0.36×0.6+0.36

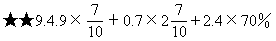
★★10.1932-499+989

★★14.32×1.25×25

★★15.8.88×125