8.[题例]有一根圆柱形木料，如果沿着水平方向将它锯成3小段，表面积则增加113.04平方厘米；如果沿着上、下底面直径将它竖着切成相同的两块，表面积则增加120平方厘米。这个圆柱形木料的体积是多少立方厘米？

[思路点拨]同学们都知道，圆柱的体积=底面积×高。可是，题中没有直接告诉我们底面积、高是多少，怎样求底面积(或底面直径)和高呢？我们可以根据已知条件画出两个示意图来进行分析。观察图1，将圆柱形木料沿着水平方向锯一次，增加的面积为木料底面积的2倍。将其锯成3段，需要锯2次，增加的面积就是木料底面积的4(2×2)倍。因此，木料的底面积为113.04÷4=28.26(平方厘米)，底面半径的平方为

7.[题例]甲、乙两人共同生产一种零件，甲生产了8小时，乙生产了6小时，一共生产了312个零件。已知，乙5小时的工作量等于甲2小时的工作量。甲、乙各生产了多少个零件？

[思路点拨]假设312个零件全部给乙做，先把甲生产的8小时的工作量替换成乙做需要几小时，根据“乙5小时的工作量等于甲2小时的工作量”，甲做8小时，乙就要做8÷2×5＝20小时。

[解题过程]8÷2×5＝20(小时)

　　　　 312÷(20+6)＝12(个)

　　　　 乙：6×12＝72(个)

　　　　 甲：312-72＝240(个)

　　　 检验：240÷8＝30

　　　　　　 30×2÷5＝12

　　　　 答：甲生产了240个，乙生产了72个。

6.[题例]甲、乙两堆煤共重78吨，从甲堆运出25%到乙堆，则乙堆与甲堆的重量比是8：5.原来各有多少吨煤？

[思路点拨]甲乙两堆煤的重量分别发生了变化，但它们的总重量不变。所以我们可以先根据甲乙两堆煤的总重量和它们的重量比为8：5算出减少后甲堆煤的重量为30吨；再根据甲堆运出25%后是30吨算出甲堆原来的吨数和乙堆原来的吨数。

[解题过程]

甲堆运出后的重量：78×=30(吨)

甲堆原来的重量：30÷(1-25%)=30÷0.75=40(吨)

乙堆原来的吨数：78-40=38(吨)

答：甲堆原来有40吨煤，乙堆原来有38吨煤。

5.[题例]　 在下列长方形中画出一条线段，把它分成一个三角形和一个梯形，使它们面积的比是2：3。

[思路点拨]假想是从长方形的左上顶点向下画出一条直线，三角形和梯形的高是相等的，因此，它们面积之间的倍数关系就是底之间的倍数关系。三角形和梯形面积的比是2：3，则三角形的底：梯形的(上底+下底)=2：3，也就是必须把长方形的两长平均分成5份。

但是这样分实际很难操作。我们回顾比的基本性质，2：3=4：6，如果把两平均分成10份，不是容易一些吗？

[解题过程]： 首先将长方形的两条长平均分成10份，然后使三角形的底为4份，梯形的底为6份即可。

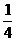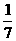4.[题例]如果※3=××，※2=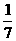×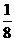；那么请你探究：※3=(　 　　 )，

※4－※4＝(　　)。

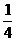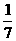[思路点拨]这是一个找规律的题目，要能顺利解答，关键是能从例子※3=××，※2=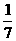×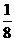中找出规律。观察题目不难发现※后是几，就依次连乘几个分子为1的分数，而且分母是从※前的分母依次向后连续的自然数。

[解题过程]

※3=××=

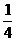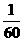
※4－※4＝×××-×××=

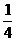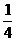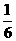3.[题例]甲、乙、丙三位小朋友各自收集了一些画片，甲收集了60张，是三人中收集最多的，以下三个只有一个是正确的，

A:甲、乙、丙三人收集张数的比是13：7：5　

B:甲收集的张数占三人张数的30%

C：甲收集的张数是总数的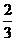倍少22张。

(1)以上准确的信息是(　 )

(2)根据以上提供的信息，请你算一算甲、乙、丙三人共有画片多少张？

[思路点拨]遇到这种题目可以用排除法进行推理。

如果A信息是正确的，那就用60÷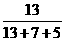 的方法求出画片总张数。由于计算结果不是整数，所以信息A错误。

如果B信息正确则可以用60÷30%=200(张)算出总张数，虽然结果为整数，但是不符合“三人中甲收集得最多”这一信息。因为如果总张数200正确，那么乙丙两人的总和也应该是140张，那么乙丙两人中张数较多的一个人，至少也是70张。140÷2=70(张)与题目条件不符。因此信息B也是错误的。

由此看来信息C该是正确的。

根据“甲收集的张数是总数的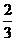倍少22张”，单位“1”未知，可以列方程解答这道题目。

[解题过程]

解：设总数是x张。

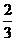x-22=60　

x=123　

答：甲乙丙三人共有画片123张。

3. 14080×0.2÷1=2816(瓶)

2. 55×40%×640=14080(只)

1.(45+50+65+55+60+50+50+54+61+60)÷10=55(只)

3.用总只数乘每只元数可以求出总元数，再除以每瓶的元数。

[解题过程]：