49.[题例]教室的门高大约2米，宽大约1米，现在将教室的门打开90度，教室的门大约扫过了多大的空间？(海安县西场镇中心小学　 许隆)

[思路点拨]教室门旋转的空间可以看作是一个半径是1米，高是2米的圆柱的体积，而“现在将教室的门打开90度”，其旋转的空间是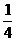个圆柱的体积。

[解题过程]

48.[题例]圆柱的半径是10厘米，侧面积是100平方厘米，它的体积是多少？

[思路点拨]这类题目同学们的正常解题思路是先求出圆柱的高，再求圆柱的体积。其实可以运用转化的思想来解题，根据圆柱体积公式的推导过程，可以把圆柱切拼成一个长方体，把圆柱原来的侧面摆放为长方体的底面，那么长方体的底面积是圆柱侧面积的一半，高就是圆柱原来底面的半径。(加图)

解题过程：100÷2×10＝500(平方厘米)。

47.[题例]上海世博会的巨大标语牌上，要用油漆涂出如下图所示的三种标点符号：句号，逗号，问号(图中阴影部分)。已知大圆半径为R，小圆半径为r，且R＝2r。若均匀用料，哪一个标点符号用的油漆最多？

[思路点拨]要求哪个标点符号用的油漆最多其实就是求阴影部分的面积哪个大，但题目中并没有告诉具体数据，乍一看无从下手，怎么办呢？别急，其实根据“大圆半径为R，小圆半径为r，且R＝2r”我们不妨假设R是4分米，则r是2分米，那么上述三种标点符号中阴影部分的面积就能很容易地求出来。

[解题过程]

句号： 4²π－2²π＝12π(平方分米)

逗号：×4²π＝8π(平方分米)

问号：×12π+2²π＝13π(平方分米)

13π＞12π＞8π

答：问号用的油漆最多。

46．[题例]如图，长方形ABCD是由上、中、下三个长方形拼成的，已知中间长方形的宽正好是上下两个长方形宽的和。那么S₁ 、S₃的面积和与S₄的面积比是(　　 )。

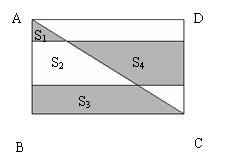
[思路点拨]我们知道：S1+S2+S3＝长方形ABCD面积的一半。而“中间长方形的宽正好是上、下两个长方形宽的和”，所以中间长方形的面积也等于长方形ABCD面积的一半，即S2+S4＝长方形面积的一半。由此我们可以进行“等价交换”而得出：S1+S2+S3＝S2+S4，即S1+S3＝S4。那么图形中，对角线下面的两个阴影部分的面积和与对角线上面的阴影部分面积相等，它们的比是1：1。

[解题过程]

S1+S2+S3＝长方形ABCD面积的一半

S2+S4＝长方形面积的一半

S1+S2+S3＝S2+S4，即S1+S3＝S4

(S1+S3)：S4＝1：1

45.[题例]一个长16厘米，宽8厘米的长方形铁皮，你能把它剪成五块，焊接成一个底面是正方形的长方体容器吗？(不许浪费)画出草图，并算出这个容器的容积是多少？

[思路点拨]

从题中要求“剪成五块，焊接成一个底面是正方形的长方体容器”我们可知剪成的铁皮的类型，一块正方形和四块完全一样的长方形，长方形的长要和正方工形的边长相等，有了这个思路，我们可把这块长方形铁皮先分成两块边长是8厘米的正方形，一块做容器有底，别一个正方形剪成四块，做周围四个面。

[解题过程]

8÷4=2(厘米)

8×8×2＝128(立方厘米)

答：这个容器的容积是128立方厘米。

44.[题例]求下图1中的阴影部分面积(单位:厘米)。

[思路点拨]阴影部分是个不规则图形，我们可以通过动态处理，使得图形变得简单。连接BD，然后旋转BC边，可以得到一个新图形，如图2所示：从图中可以看出，阴影部分面积正好等于圆面积减去里面一个最大正方形的面积。又因正方形面积和圆面积的比为2:π，从而很容易求出阴影部分的面积。

[解题过程]

圆的面积：3.14×()²＝7.065(平方厘米)

正方形的面积：7.065÷3.14×2＝4.5(平方厘米)

阴影部分的面积：7.065－4.5＝2.565(平方厘米)

43.[题例]友谊商场五一购物优惠活动：购物满200元，送100元的购物券，凭购物券加上60元以上的现金可以购买商店里的任何商品。小明帮妈妈选了一件210元的羊毛衫，得到100元的购物券，然后又添90元买了一个皮包，请你算算，小明实际购物相当于打几折？

[思路点拨]折数=现价÷原价。小明可以用妈妈实际付出的元数除以这两样货物原有的标价之和。

解题过程：(90+210)÷(210+100+90)=75%

答：小明实际购物相当于打七五折。

42.[题例]一只装有水的长方体玻璃杯，底面积是60平方厘米，水深8厘米。现将一个底面积是12平方厘米的圆柱体铁块竖放在水中(直到底部)，仍有一部分铁块露在水面上，现在水深多少厘米？

[思路点拨]因为铁块已经到了底部，所以这时水所占据的地面积不再是60平方厘米，而是(60-12)平方厘米，水的体积并没有变化，60×8÷(60-12)可以求出水现在的高度。

解题过程：60×8÷(60-12)=10

答：现在水深10厘米。

41.[题例]如右图，东西、南北两条路交叉成直角，甲距路口中心(o点)1500米。甲由南向北，乙路口中心由西向东，同时行走。5分钟后，甲尚未走到路口，两人离路口中心的距离相等；又走45分钟后，两人离路口的距离又相等。求甲、乙两人每分钟各行多少米？

[思路点拨]由“甲距路口中心1500米”“5分钟后，甲尚未走到路口，两人离路口中心的距离相等”可知，甲5分钟行的路程加上乙5分钟所行的路程是1500米。得出，甲乙的速度和是1500÷5=300。再由“又走45分钟后，两人离路口的距离又相等。”可知，甲45分钟的路程相当于乙55分钟的路程，路程一定时速度和时间成反比例，甲乙的时间比是45：55=9：11，所以他们的速度比是11：9，此题就转化成为按比例分配应用题。

解题过程：1500÷5=300(米)

45：(45+5+5)=9：11

300×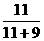=165(米)

300×=135(米)

答：甲每分钟行165米，乙每分钟行135米。

40.[题例]小明定居在美国纽约，妈妈定居在北京。2009年12月31日晚上7时45分小明在纽约给妈妈打电话，祝妈妈新年快乐。妈妈一看正好是2010年1月1日早上8时45分。春节前，2月1日晚上9时30分，妈妈打电话给小明，叫他回北京过年。小明春节回家时花了500美元给妈妈买了两件礼物：一件大衣200美元和一个项链300美元。妈妈一打听，这件大衣相当于人民币1366元。

(1)妈妈打电话给小明时正好是纽约什么时间？

(2)小明给妈妈买的项链相当于人民币多少元？

[思路点拨](1)根据“2009年12月31日晚上7时45分小明在纽约给妈妈打电话，祝妈妈新年快乐。妈妈一看正好是2010年1月1日早上8时45分。”可知纽约时间+13小时=北京时间，从而可以推算妈妈打电话给小明时纽约的时间。

　　　　 　(2)根据“一件大衣200美元”和“这件大衣相当于人民币1366元”可以知道美元与人民币的汇率，从而可以求到项链相当于人民币多少元。

[解题过程](1)2月1日晚上9时30分－13小时=1月31日早上8时30分

　　　　　 答：妈妈打电话给小明时正好是纽约1月31日早上8时30分。

　　　　 (2)1366÷200×300=2049(元)

　　　　　 答：小明给妈妈买的项链相当于人民币2049元。