54.[题例]如图，一些小球按下面方式摆放，照这样的规律，第五堆小球共(　　　 )个，第十堆小球共有(　　　 )个。

[思路点拨]观察图形，第一堆1个小球，第二堆第一行1个小球，第二行2个小球，一共(1+2=)3个小球；第三堆第一行1个小球，第二行2个小球，第三行3个小球，一共(1+2+3=)6个小球；第四堆第一行1个小球，第二行2个小球，第三行3个小球，第四行4个小球，共(1+2+3+4=)10个球；由此可以推断第五堆共有(1+2+3+4+5=)15个小球，第十堆共有(1+2+3+4+…+10=)55个小球。

[解题过程]

第五堆小球：1+2+3+4+5=15(个)

第十堆小球：1+2+3+4+…+10=55(个)

53.[题例]华新建筑公司有两个工程队，甲队有28人，乙队有22人，现需使甲、乙两队的人数比是3:2，下面给出了几种方案，请你先判断方案的可行性(可行的打“√”，不可行的打“×”)，再算出增加、减少或甲、乙两队之间的调整人数。

[思路点拨](1)由甲队有28人，要使甲乙两人的人数比是3:2，我们可判断方案(3)(4)不可行(28不是3的倍数)；(2)由甲队有28人，乙队有22，可知甲乙两队的比的比值是，要使甲乙两队的比的比值为，比值增加，甲队要增加人数，，从而可判断(1)(5)方法不可行，可行的只有方案(2)和(6)。

[解题过程]

6.7×2＝13.4(元)

　　　 答：小明带了13.4元。

6.2+0.5＝6.7(元)

3.1×2＝6.2(元)

2.8+0.8－0.5＝3.1(元)

52.[题例]小明去文具店买了1支钢笔后，发现所用的钱比所带的总钱数的一半多0.5元；接着买了1支圆珠笔，所用的钱比买钢笔后余下的钱的一半少0.5元；又买了2.8元的本子，最后剩下0.8元。小明带了多少元钱？

[思路点拨]这题我们采用倒推的策略，从“又买了2.8元的本子，最后剩下0.8元”可知，买圆珠笔后剩下了(2.8+0.8)元，接着从“接着买了1支圆珠笔，所用的钱比买钢笔后余下的钱的一半少0.5元”中可知，如果买圆珠笔的钱正好是买钢笔余下的钱的一半的话，那么买钢笔剩下的钱的一半就是(2.8+0.8－0.5)元，即3.1元，买钢笔剩下的钱就是3.1×2＝6.2(元)，然后从“买了1支钢笔后，发现所用的钱比所带的总钱数的一半多0.5元”中，如果买了1支钢笔后，发现所用的钱正好所带的总钱数的一半的话，就应该是6.2+0.5＝6.7(元)

[解题过程]

51.[题例]某渔船队出海捕鱼，如果出海后是好天，那么收益10000元；如果出海后天气变坏，将损失7000元。无论出不出海，每月都要承担2000元的正常消耗费。据气象部分预测，六月份好天气的可能性有40%，坏天气的可能性有60%。如果你是队长，你认为六月份是否应该出海捕鱼？(西场镇中心小学　　 崔艳丽)

[思路点拨]如果六月份每天出海捕鱼共30次，好天气有30×40%＝12次，可得收益：10000×12＝120000元；遇到坏天气有30×60%＝18次，将损失：7000×18＝126000元，共计损失126000－120000+2000＝8000元。由此看出，六月份每天出海捕鱼共损失8000元，比不出海捕鱼只消耗2000元损失更大，而且天气恶劣，人生安全得不到保障，不值得冒这样的险。

[解题过程]

30×40%＝12次　　　　 10000×12＝120000元

30×60%＝18次　　　　 7000×18＝126000元

126000－120000+2000＝8000元　　　　 8000＞2000

答：不应该出海捕鱼。

50.[题例]计算图中阴影部分的面积。(单位：厘米)

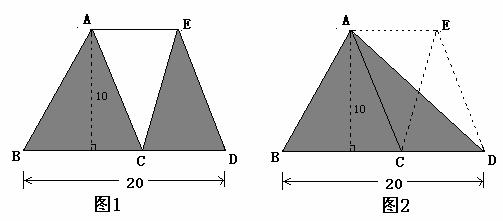
[思路点拨]图中阴影部分的面积由两个三角形组成，但是三角形的底不知道，无法分别求出三角形的面积，但图中告之了两个三角形底的和，可以试着将三角形转化到一起。连接A、D，(如图2所示)，发现三角形ACD和ECD等底等高，可以把三角形ECD的面积转化为三角形ACD的面积，所求阴影部分的面积就是△ABD的面积。

[解题过程]20×10÷2＝100(平方厘米)。

3.14×1×1×2×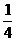＝1.57(立方米)

答：教室的门大约扫过了的空间是1.57立方米。