
题目列表(包括答案和解析)
4、注意两位数ab与ba分别可表示成10a+b以及10b+a,然后按题意列式求解。
3、设这个两位数为ab,a是十位数字,b是个位数字,那么这个两位数可以写成10a+b。同理,中间加一个0所得的3位数可以写成100a+b。于是由题给条件可列出下面的式子,100a+b=7(10a+b),从而100a+b-b-70a=70a+7b-b-70a,这就是30a=6b,因此b=5a。注意到a、b只能取小于10的数即可求出它们的值。
2、解法一:因为商与除数相同,所以商与除数的乘积是一个平方数,而且这个平方数一定不超过239(想一想理由是什么?)。然后判断不超过239的平方数中,哪个平方数是符合题目要求的(这里要用到除法中除数与余数的大小关系)。由此即可求出除数。解法二:设除数是x,那么根据条件,并把除法改用乘法(想想怎样用乘法对除法作验算)写出来就可得到239=x2+x-1。等式两边都加1得239+1=x2+x,这就是x(x+1)=240。把这个式看成是两个连续自然数的积是240,你应该知道怎样求x了。
1、(1)仿例1(1)题的方法即可;(2)反复用例1(1)题的做法,直到找出规律为止;(3)这是由两个数列凑合而成的,对每个数列用上述方法;(4)它也是由两个数列合成的,做法与上一小题同。
15、10条直线最多可以把平面分成几部分?
习题二提示及部分解答
14、仿照例6的方法计算13+23+33+…+n3。
13、3个三角形最多可把整个平面分成多少个区域?4个三角形呢?10个三角形呢?
12、连结圆周上任意两点的线段叫做弦,直径正好就是经过圆心的弦。一个圆被一条直径和一条弦划分,最多可分成4个区域。一个圆被2条直径和一条弦划分,最多可分成7个区域。那么,一个圆若被一百条直径和一条弦来分,最多可分成多少个区域呢?
11、一个分数在约分前分子分母的和为108,如果分子加上15,分母加上12再作约分,恰好得到 ,求原来的分数化成最简分数应是多少?
,求原来的分数化成最简分数应是多少?
10、计算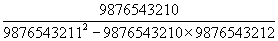 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com