14、先证明对任何自然数n有

　(n+1)⁴=n⁴+4n³+6n²+4n+1，　(1)

由此推出

　(n+1)⁴-n⁴=4n⁴+6n²+4n+1。　(2)

然后利用(2)式分别取n为1，2，…，n-1，n得出n个等式。把这些等式左、右两边分别相加，然后利用(2.15)式及关于前n个自然数的和的公式就得出要求的计算公式了。详细过程参见例6。

　另解：此题还有一个特殊的解法。直接计算可得

　1³ 　 =1²；　 1³+2³ 　 =3²；

　1³+2³+3³ 　 =6²；　1³+2³+3³+4³=10²；

　1³+2³+3³+4³+5³=15²；

　… … … …

　注意到数列1，3，6，10，15，…， 　(1)

它的规律是：其中第n个数等于1+2+…+n，即可得出

　1³+2³+…+n³=(1+2+…+n)²=(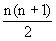)²。　(2)

在寻找数列(1)中第n个数的规律时，仍然要用到正文中例1给出的方法，即把(1)写成

并注意3=1+2，6=1+2+3，10=1+2+3+4，15=1+2+3+4+5等等。

13、注意先研究一个及两个三角形的情形。方法与上题类似。

12、解法一：先研究3条直径和1条弦最多可把圆分成几个区域，结论是10个，再由数列4，7，10，…的规律求出问题的答案。

　解法二：先考虑一百条直径把圆分成多少个区域(注意每加一条不同的直径，划分的区域多出2个)，然后再添上一条弦，看它能增加最多多少个区域。

11、假设约分前分子为a，分母为b，那么由题意得到

　a+b=108　　 (1)

　= 　(2)

注意到(2)式就是b+12=2×(a+15)，即有b+12-2a-12=2a+2×15-2a-12，这就是

　b-2a=18。　 (3)

(1)式表示a与b的和是108，而(3)式表示b比a的2倍还多18，现在求a，b就容易了。

10、此题与第7、8两题类同，千万不要直接计算。注意到分子、分母中四个数的共同点，可以设a=9876543210，于是原式变为，用分配律把分母的值算出来即可。

9、注意其中最小与最大的两个数的和是61-49=12。由此再利用2+3+4+5+6+7+8+9+10=54比61小推出，最小，最大两数只可能是1和11。最后注意1+2+3+4+5+6+7+8+9+10+11=66。剩下的推理由你自己完成。

8、做法与上题同，只不过这次应假设a=+…+，于是原式变为(1+a)×(a+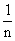)-(1+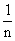a+)×a。

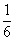7、算式里有4个括号，4个括号中共同有的是+++，就设a=+++，题目中的式子就变成(1+a)×(a+)-(1+a+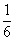)×a，利用分配律两次(参考(2.8)式的计算过程)就可以算出它的值。

6、根据条件列出以下式子：

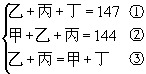
由①，②两式推出丁=甲+3，代入③式得

　2甲=乙+丙-3 　④

把②式两边都乘以2得

　2甲+2乙+2丙=288　 ⑤

用④式代替⑤式中的2甲，就可求出乙+丙的值。再利用③式就可求出四班人数总和。

5、这种几个字母轮换出现的式子通常用加法去做，即把3个式子的左边和右边分别相加，这就得到4x+4y+4z=44，由此即可求出x+y+z的值。