题目列表(包括答案和解析)
9.若有8分和15分的邮票可以无限制地取用，但某些邮资如：7分、29分等不能刚好凑成，那么只用8分和15分的邮票
不能凑成的最大邮资是________。
10.
的末两位数是________。
11.4只小鸟飞入4个不同的笼子里去，每只小鸟都有自己的一个笼子(不同的鸟，笼子也不相同)，每个笼子只能飞进一只鸟。若都不飞进自己的笼子里去，有________种不同的飞法。
12.甲、乙两船分别在一条河的A，B两地同时相向而行，甲顺流而下，乙逆流而行。相遇时，甲、乙两船行了相等的航程，相遇后继续前进，甲到达B地，乙到达A地后，都立即按原来路线返航，两船第二次相遇时，甲船比乙船少行1千米。如果从第一次相遇到第二次相遇时间相隔1小时20分，则河水的流速为每小时_______千米。
=________。
2.一个千位数字是1的四位数，当它分别被四个不同的质数相除时，余数都是1，满足这些条件的最大的偶数是 ____。
3.有两个三位数，它们的和是999，如把较大数放在较小数的左边，点一个小数点在两数之间所成的数，正好等于把较小数放在较大数的左边，点一个小数点在两数之间所成的数的6倍，那么这两个数的差(大减小)是 ________。
4.一千个体积为1立方厘米的小立方体合在一起成为一个边长为10厘米的大立方体，表面涂油漆后再分开为原来的小立方体，这些小立方体中至少有一面被油漆涂过的数目是_______。
5.某班有50名学生，参加语文竞赛的有28人，参加数学竞赛的有23人，参加英语竞赛的有20人，每人至多参加两科，那么参加两科的最多有_______人。
6.甲、乙两人进行百米赛跑，当甲到达终点时，乙在甲后面20米处；如果两人各自的速度不变，要使甲、乙两人同时到达终点，甲的起跑线应比原来的起跑线后移_______米。
7.一水池有一根进水管不断地进水，另有若干根相同的抽水管。若用24根抽水管抽水，6小时即可把池中的水抽干；若用21根抽水管抽水，8小时可将池中的水抽干。若用16根抽水管抽水，_______小时可将池中的水抽干。|
8.如右图, P为平行四边形ABCD外一点，已知三角
形PAB与三角形PCD的面积分别为7平方厘米和3平
方厘米，那么平行四边形ABCD的面积为_______平方厘米。 |
 |
7.有一钟表，每小时慢2分钟，早上8点时，把表对准了标准时间，当中午钟表走到12点整的时候，标准时间为_____。
8.地震时，地震中心同时向各个方向传播出纵波和横波，纵波的传播速度是3.96千米/秒，横波的传播速度是2.58千米/秒。某次地震，地震检测点用地震仪接受到地震的纵波之后，隔了18.5秒钟，接受到这个地震的横波，那么这次地震的地震中心距离地震检测点________千米(精确到个位)。
9.一块冰，每小时失去其重量的一半，八小时之后其重量为 
千克，那么一开始这块冰的重量是________千克。
10.五年级一班有32人参加数学竞赛，有27人参加英语竞赛，有22人参加语文竞赛，其中参加了数学和英语两科的有12人，参加了语文和英语的有14人，参加了数学和语文两科的有10人，那么五年级一班至少有________人。
11.有2000盏亮着的电灯，各有一个拉线开关控制着。现按其顺序编号为1，2，3，…，2000，然后将编号为2的倍数的灯线拉一下，再将编号为3的倍数的灯线拉一下，最后将编号为5的倍数的灯线拉一下，三次拉完之后，亮着的电灯有________盏。
12.有25张纸片，每张纸片的正面用红色铅笔任意写上一个不超过5的自然数，反面用蓝色铅笔任意写上一个也是不超过5的自然数，唯一的限制是：红色数字相同的任何两张纸片上，所写的蓝色数字一定不能相同。现在把每张纸片上的红、蓝两个整数相乘，这25个积的和为________。
=________。
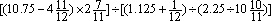2.原有男、女同学325人，新学年男生增加25人；女生减少5%，总人数增加16人，那么现有男同学________人。
3.一商店以每3盘16元的价格购进一批录音带，又从另一处以每4盘21元的价格购进比前一批加倍的录音带。如果以每3盘K元的价格全部出售可得到所投资的20%的收益，则K值是________。
4.在除13511，13903及14589时能剩下相同余数的最大整数是________。
5.试将20表示成一些合数的和，这些合数的积最大是________。|
6.在1×2×3×...×100的积中，从右边数第25个数字是___。
7.如右图所示, 角AOB=90o，C为AB弧的中点，已知阴影甲的面积为
16平方厘米，则阴影乙的面积为________平方厘米。
8.各数位上数码之和是15的三位数共有_____个。 |
 |
7.a是由2000个9组成的2000位整数，b是由2000个8组成的2000位整数，则a×b的各位数字之和为________。
8.四个连续自然数，它们从小到大顺次是3的倍数、5的倍数、7的倍数、9的倍数，这四个连续自然数的和最小是____。
9.某区对用电的收费标准规定如下：每月每户用电不超过10度的部分，按每度0.45元收费；超过10度而不超过20度的部分，按每度0.80元收费；超过20度的部分，按每度1.50元收费。某月甲用户比乙用户多交电费7.10元，乙用户比丙用户多交3.75元，那么甲、乙、丙三用户共交电费________元(用电都按整度数收费)。
10.一辆小汽车与一辆大卡车在一段9千米长的狭路上相遇，必须倒车，才能继续通行。已知小汽车的速度是大卡车的速度的3倍，两车倒车的速度是各自速度的 
；小汽车需倒车的路程是大卡车需倒车的路程的4倍。如果小汽车的速度是50千米/时，那么要通过这段狭路最少用________小时。
11.某学校五年级共有110人，参加语文、数学、英语三科活动小组，每人至少参加一组。已知参加语文小组的有52人，只参加语文小组的有16人；参加英语小组的有61人，只参加英语小组的有15人；参加数学小组的有63人，只参加数学小组的有21人。那么三组都参加的有________人。
12.有8级台阶，小明从下向上走，若每次只能跨过一级或两级，他走上去可能有________种不同方法。
=________。
2.1到2000之间被3，4，5除余1的数共有________个。
3.已知从1开始连续n个自然数相乘，1×2×3×…×n，乘积的尾部恰有25
个连续的0，那么n的最大值是____ 。
4.若今天是星期六，从今日起102000天后的那一天是星期________。
5.如右图，在平行四边形ABCD中，AB=16，
AD=10，BE=4，则FC=________。
6.所有适合不等式 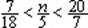 的自然数n
之和为________。 |
 |
13、甲乙两人对一根7米长的木棍涂色，首先甲从木棍的一端开始涂黑5厘米，间隔5厘米不涂色，然后再涂黑5厘米，如此交替下去直到最后。然后，乙仍从同一端点开始，先留7厘米不涂色，接着涂黑7厘米，再留7厘米不涂色，这样交替到最后。最后按颜色分界线锯断，求共锯成多少段？其中没有涂色的木棍有多少段、总长是多少？
12、小明把如下12个数各写在一张纸条上，再把纸条捏成团，从中拣出一个纸团丢掉，把剩下的11个纸团分成两组，打开一看，甲组中的几个数是互不相同的奇数，且乙组中各数之和恰好是甲组各数之和的4倍，求：(1)丢掉的纸团上写的是哪个数？(2)甲组中有几个数？是哪几个数？那12个数是：5，6，7，9，10，11，11，11，11，12，12，14。
11、1991个1991依次连接起来成一个多位数，求这个数被7除的余数。
10、下面5组数中只有一组数不是方程3785x-468y=121的解，请指出这组数来。
A、x=21257，y=171918； B、x=20321, y=164348； C、x=23597, y=190843；
D、x=22941, y=186737； E、x=22661, y=183273。
9、若干个数排成一行，开头两个数是1与3，从第二个数开始，每个数的4倍等于它左右两边两数之和。(1)求这个数列中第80个数及第123个数被3除的余数及被5除的余数。(2)1785与1988这两个数是否在这列数中？
8、一个学生扳手指头数数，按照下述规定进行：从中指开始数1，依次按食指、大拇指、食指、中指、无名指、小指、再折回无名指、中指，以下与此相同。问：他数到1991时扳的是哪个手指？
7、求1×3×5×7×9×11×13×…×1991的最后两位数字。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com