4．跑道长是200米

　第一次相遇甲、乙共跑了半圈，其中甲跑了60米．设半圈跑道长为x米，乙在俩人第一次相遇时跑了x-60米．从出发到甲乙第二次相遇共跑了3个半圈长，由于他俩匀速跑步，在3个半圈长里乙应跑3(x-60)米，而这个距离恰好是乙跑一圈还差80米，即2x-80米，所以

　3(x－60)＝2x-80

　3x-180=2x-80

　x＝100

　2x=2×100=200(米)

　故圆形跑道的长是200米．

3．B得98分

　由D得分是五人的平均分知，D比A得分高，否则D成为五人中得分最低的，就不能是五人的平均分，由此得到五人得分从高到低依次是B、E、D、C、A．

　由C得分是A与D的平均分，因为A是94分，94是偶数，所以D的得分也应是偶数，但D不能得100分，否则B得分超过100分；D=98分，则C=96分，E=98分，B=98×5-(98+96+94+98)=104分，超过100分，不可能；所以D=96分，C=95分，E=97分，B得分是

　96×5-(97+96+95+94)=98(分)

2．小明5岁，妈妈32岁，爸爸36岁，爷爷74岁

　妈妈与小明年龄之和：

　(147+38)÷(2×2+1)=37(岁)

　小明的年龄：(37-27)÷2=5(岁)

　妈妈的年龄：37-5=32(岁)

　爷爷的年龄： 37×2=74(岁)

　爸爸的年龄：74-38=36(岁)

1．取了6次后，红球剩9个，黄球剩2个．

　设取了x次后，红球剩9个，黄球剩2个．

　5x+9=(4x+2)×1.5

　5x+9＝6x+3

　x=6

　所以取6次后，红球剩9个，黄球剩2个．

9．21

　每个车间抽出3名装卸工，共抽出3×5=15人，每辆车上有3人，共需3×3=9人，这样可节约15-9=6(人)．这时A有3人，B有2人，C有4人，D有0人，E有5人．再从A、B、C、E各抽出2人，每车上2人，这样又可省去2×4-2×3=2人．这样每辆车跟5人，共15人，A有1人，B有0人，C有2人，E有3人，D还是0人．共需装卸工：

　5×3+1+2+3=21(人)

　第二次从乙容器里倒出一部分给甲容器，并不改变乙容器的酒精浓度，所以乙容器里酒精浓度是第一次甲容器倒入一部分纯酒精而得到的，因此乙容器中酒精与水之比是：

　20%∶(1-20%)=1∶4

　那么第一次从甲容器里倒出100克给乙容器，则乙容器中纯酒精与水之比恰好是：

　100∶400=1∶4

　第二次倒后，甲容器里酒精与水之比是

　70%∶(1-70%)=7∶3

　设第二次从乙容器中倒出x克酒精溶液，则第二次倒后，甲容器有纯酒 　

　所以第二次从乙容器里倒入甲容器的混合溶液是144克．

8．38

　由题意知甲乙两人合作30天可以完成这项工作．甲做45天，比30天多15天，乙可少做

　30-18=12(天)

　说明甲做15天相当于乙做12天．

　现在甲做20天，比30天少10天，这10天的工作量让乙来完成，需要天数：

　乙还需要单独做：

　30+8=38(天)

7．1，3，3

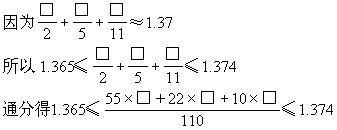
　于是有150.15≤55×□+22×□+10×□≤151.14

　由于□里的数是整数，所以

　55×□+22×□+10×□=151

　只有 55×1+22×3+10×3=151

　所以□里数字依次填1，3，3．

6．10

　这道题没有限制砝码只能放在天平的同一秤盘上，因此天平两边的秤盘上都可以放砝码，尽管只有2克、3克、6克砝码各一个，但是如果天平一边是2克，另一边是3克，就可称出1克重的物体，如果它俩放在同一边又可称出5克重的物体．同理，2克与6克砝码可称出4克或8克重的物体；3克与6克砝码可称出3克或9克重的物体，其中3克重物体可以直接用3克砝码称出；用2克、3克和6克可称出7克、5克、1克、11克重的物体；所以用这三个砝码可称出1、2、3、4、5、6、7、8、9、11克共10种不同重量的物体．

5．19平方厘米

　所求图形是不规则图形，通过分割可以很容易求出图中标出1、2、3、4、5、6、7图形的面积，用整个大长方形面积减去这7个图形的面积即为所求，所以不规则图形面积为：

　8×6-3×2÷2×3-(1+3)×3÷2-2×4÷2-(2+4)×1÷2-(3+4)×2÷2

　=(19平方厘米)

4．30

　因为4=1×4=2×2，有4个约数的数一定能表示成a³或ab，a、b是质数．

　对于a³，只有a=3时，a³=27是两位数，即有1个数符合条件．

　对于ab，当a=2，b=5、7、11、13、17、19、23、29、31、37、41、43、47时符合条件，有13个；当a=3，b取大于3且小于37的质数时，符合条件，有9个；同理当a=5时有5个；a=7时有2个．则自然数中恰有4个约数的所有两位数的个数是：

　1+13+9+5+2=30(个)