6.960

　对于A有5种着色方法，B与A相邻，有4种着色方法；C与A相邻，它可以与B的颜色相同，因此C有4种着色方法；同理可以知D有4种着色方法，E有1 种着色方法，F有3种着色方法，共有：

　5×4×4×4×1×3= 960(种)

5.大油桶18个，小油桶22个.

　假设40个油桶都是大桶，则共装油200千克，而小桶装油0千克，大桶比小桶共多装油200千克，比条件给的差数多了200-24=176千克，多的原因是把小桶看成了大桶.若把40个大桶中的一部分换成小桶，则每把一个大桶换成一个小桶，大桶装油总数就减少了5千克，小桶装油就增加了3千克，所以大桶比小桶多装的千克数就减少了5+3=8千克，那么需要把多少个大桶换成小桶呢？列式为

　(5×4-24)÷(5+3)=22(2个)……小桶个数

　40-22=18(个)……大桶个数.

4.12

　设阴影面积的长为a，宽为b，则面积为20亩的耕地的长与宽可以分别

　a×b=15×16÷20=12(亩)

3.129

9的公约数，为了使装瓶数尽可能少，a取15、42、9的最大公约数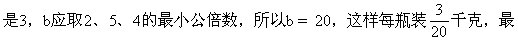 少要用的瓶数：

　 　=50+64+15

　=129(瓶)

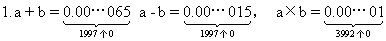　 　a÷b=1.5.

2.21972

　横放需1997×6根，竖放需1998×5根，共需：

　1997×6+1998×5

　=1997×(6+ 5)+ 5

　=21972(根)

4．如图，四个圆相互交叉，它们把四个圆面分成13个区域．如果在这些区域上(加点的)分别填上6至18的自然数，然后把每个圆中的数各自分别相加，最后把这四个圆的和相加得总和，那么总和最大可能是多少？

模拟试卷36

3．有一根6厘米长的绳子，它的一端固定在长是2厘米、宽是1厘米的长方形的一个顶点A处(如图)，让绳子另一端C与边AB在一条线上，然后把它按顺时针方向绕长方形一周，绳子扫过的面积是多少？

2．在黑板上写出3个整数分别是1，3，5，然后擦去一个换成其它两数之和，这样操作下去，最后能否得到57，64，108？为什么？

1．一个人以相同的速度在小路上散步，从第1棵树走到第13棵树用了18分，如果这个人走了24分，应走到第几棵树？

10．一次足球赛，有A、B、C、D四队参加，每两队都赛一场．按规则，胜一场得2分，平一场得1分，负一场得0分．比赛结果，C队得5分，A队得3分，D队得1分，所有场次共进了9个球，C队进球最多，进了4个球，A队共失了3个球，B队一个球也没进，D队与A队比分是2∶3，则D队与C队的比分是______．