
题目列表(包括答案和解析)
30、
Ⅰ(14分)在群体中位于某同源染色体同一位置上的两个以上,决定同一性状的基因称为复等位基因,如控制ABO血型的基因。在家兔的常染色体上有一系列决定毛色的等位基因: A、a1、a2、a。
A基因对a1、a2、a为显性,a1基因对a2、a为显性,a2对a为显性。A基因系列在决定家兔毛皮颜色时其表现型与基因型的关系如下表:
|
毛皮颜色表现型 |
基因型 |
|
全色 |
A
|
|
青旗拉 |
a1 |
|
喜马拉扬 |
a2 |
|
白化 |
aa |
请回答下列问题:
(1)家兔皮毛颜色的基因型共有 种,其中纯合体有 种。
(2)若一只全色雄兔和一只喜马拉扬雌兔多次交配后,子代全色:青旗拉=1:1,则两只亲本兔的基因型分别为 、 。
(3)若有一只喜马拉扬雄兔和多只其他各色的雌兔,如何利用杂交方法检测出喜马拉扬雄兔的基因型?(写出实验思路和预期实验结果即可)
Ⅱ、(10分)番茄叶型正常叶(A)和马铃薯叶(a)为一对相对性状,且控制叶型的基因位于常染色体上。以纯合正常叶型的第6号染色体为三体(2n+1)的植株为母本,以马铃薯叶型的正常植株(2n)为父本进行杂交,试问:
(1)假设a基因在第6染色体上,F1群体中出现的基因型及其比例为 ;使F1群体的三体植株与马铃薯叶型的正常番茄杂交,F2的叶型种类和比例为 ;三体与正常个体比例为 。
(2)假设a基因不在第6染色体上,使F1群体的三体植株与马铃薯叶型的正常番茄杂交,F2的叶型种类和比例为 ;三体与正常个体比例为 。
方案Ⅰ:取该红色粉末溶于足量稀硝酸中,观察溶液颜色变化。
方案Ⅱ:取该红色粉末溶于足量稀硫酸中,观察是否有残渣。
方案Ⅲ:装置如图所示:(夹持仪器略去)

试回答下列问题:
(1)请分别评价方案Ⅰ和方案Ⅱ是否合理(填“是”或“否”),若不合理,请简述其原因:
方案Ⅰ: ;
方案Ⅱ: 。
(2)方案Ⅲ中,实验前应检验装置气密性,请简述其操作方法:
。
(3)实际上,方案Ⅲ的装置尚存在明显的缺陷,应在A和B之间添加 。
(4)方案Ⅲ中,若要测定红色粉末的成分,至少需要测定下列哪些物理量 (填序号)。
①反应前红色粉末与硬质玻璃管的总质量 ②实验前干燥管的质量
③完全反应后红色粉末与硬质玻璃管的总质量 ④硬质玻璃管的质量
⑤锌粒质量 ⑥稀硫酸的物质的量浓度
⑦实验后干燥管的质量
29、
Ⅰ、(6分)秋末植物的叶片衰老时,在叶柄基部开始形成离层(如甲图所示),而后从植物体上脱落。离层部位细胞相关的生命活动如图乙所示。请据图回答下列问题:

(1)根据乙图可知,叶柄基部离层的产生,与 激素有密切关系。
(2)在植物激素的作用下,细胞核中的有关基因进行表达,表达产物A最终通过细胞膜
的 作用分泌到细胞外。这一过程能够证明生物膜具有的结构特点是 。
(3)该过程分泌到细胞外的物质,对离层形成所起的作用是 。
(4)进一步的研究表明,叶柄基部离层的形成,还与 等其他激素有关,这说明植物生命活动的调节是 。
Ⅱ、(6分)据研究,器官的脱落和生长素也有关。下面是有关的实验现象,请根据现象回答问题。
(1)切去植物的叶片,残留的叶柄基部很快形成离层,叶柄脱落。但如在去叶片后的伤口处(远轴端;参见上图)涂以含生长素的羊毛脂,则会延迟叶柄的脱落。
(2)但是用生长素处理的部位不同时得到不同的结果,将生长素施加到离层区靠茎的一面(近轴端;参见上图)时,反而促进脱落。
 Addicott等提出脱落的有关学说来解释这一实验结果。决定器官脱落的是离层区两边的
,而不是生长素的绝对含量。
Addicott等提出脱落的有关学说来解释这一实验结果。决定器官脱落的是离层区两边的
,而不是生长素的绝对含量。
当 时,离层不形成,不发生脱落;
当 时,离层形成,加速脱落;
Ⅲ、(10分)在人和动物体内由特殊腺体和细胞分泌的物质,能调节人体各项生理活动。请据图回答:
(1)若B代表肝脏细胞,E代表延髓细胞,D代表血管:
当人体处于饥饿时,D中 (激素)含量上升,该激素与E共同作用,使B中的 分解维持正常的血糖浓度。
(2)A突触小体释放的递质与突触后膜结合,导致突触后膜神经元产生抑制。下图示突触前膜释放递质时,突触后膜接受递质后的膜电位状况以及兴奋的传导方向。其中正确的是( )

(3)为研究促甲状腺激素(TSH)分泌的影响因素,研究者从刚宰杀的大白鼠体内分离新鲜的下丘脑和脑垂体。然后把这些细胞单独或一起培养于含有或不含有甲状腺激素的培养基中,培养后测定培养基内TSH的浓度,结果如下:

根据实验结果,可以得到的结论有:
①下丘脑不能分泌TSH;垂体能分泌TSH;
②_______________________________________。
③_______________________________________。
20.(本小题满分14分)
已知函数 .
.
(Ⅰ) 若函数 在
在 上为单调增函数,求
上为单调增函数,求 的取值范围;
的取值范围;
(Ⅱ) 设 ,
,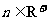 ,且
,且 ,求证:
,求证: .
.
(考生务必将答案答在答题卡上,在试卷上作答无效)
北京市东城区2009-2010学年度第二学期综合练习(二)
19.(本小题满分13分)
已知数列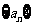 的前
的前 项和为
项和为 ,
, ,
, ,设
,设 .
.
(Ⅰ)证明数列 是等比数列;
是等比数列;
(Ⅱ)数列 满足
满足
 ,设
,设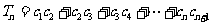 , 若对一切
, 若对一切 不等式
不等式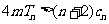 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
18.(本小题满分13分)
已知抛物线的焦点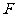 在
在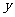 轴上,抛物线上一点
轴上,抛物线上一点 到准线的距离是
到准线的距离是 ,过点
,过点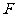 的直线与抛物线交于
的直线与抛物线交于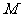 ,
, 两点,过
两点,过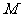 ,
, 两点分别作抛物线的切线,这两条切线的交点为
两点分别作抛物线的切线,这两条切线的交点为 .
.
(Ⅰ)求抛物线的标准方程;
(Ⅱ)求 的值;
的值;
(Ⅲ)求证: 是
是 和
和 的等比中项.
的等比中项.
17.(本小题满分14分)
如图,四棱锥 中,底面
中,底面 是直角梯形,
是直角梯形,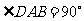 ,
,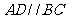 ,
, 侧面
侧面 ,△
,△ 是等边三角形,
是等边三角形, ,
,  ,
, 是线段
是线段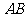 的中点.
的中点.
 (Ⅰ)求证:
(Ⅰ)求证: ;
;
(Ⅱ)求四棱锥 的体积;
的体积;
(Ⅲ)求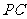 与平面
与平面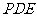 所成角的正弦值.
所成角的正弦值.
16.(本小题满分13分)
袋中装着标有数字1,2,3,4的小球各3个,从袋中任取3个小球,每个小球被取出的可能性都相等.
(Ⅰ)求取出的3个小球上的数字互不相同的概率;
(Ⅱ)用 表示取出的3个小球上所标的最大数字,求随机变量
表示取出的3个小球上所标的最大数字,求随机变量 的分布列和均值.
的分布列和均值.
15. (本小题满分13分)
在 中,角
中,角 ,
,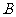 ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,
,
 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若 ,
, ,求
,求 的值.
的值.
14. 已知数列 中,
中, 是其前
是其前 项和,若
项和,若 ,
, ,
, ,
,
且 ,则
,则 _______________,
_______________, _______________.
_______________.
13. 在函数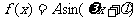
 的一个周期内,当
的一个周期内,当 时有最大值
时有最大值 ,当
,当 时有最小值
时有最小值 ,若
,若 ,则函数解析式
,则函数解析式 =
.
=
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com