9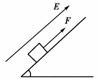．(2010·金华模拟)如图所示，在绝缘的斜面上方，存在着匀强电场，电场方向平行于斜面向上，斜面上的带电金属块在平行于斜面的力F作用下沿斜面移动．已知金属块在移动的过程中，力F做功32 J，金属块克服电场力做功8 J，金属块克服摩擦力做功16 J，重力势能增加18 J，则在此过程中金属块的(　)

A．动能减少10 J　 　　　　　　　　　 B．电势能增加24 J

C．机械能减少24 J　 　　　　　　　　 D．内能增加16 J

答案：AD

解析：由动能定理可知ΔE_k＝32 J－8 J－16 J－18 J＝－10 J，A正确；克服电场力做功为8 J，则电势能增加8 J，B错误；机械能的改变量等于除重力以外的其他力所做的总功，故应为ΔE＝32 J－8 J－16 J＝8 J，C错误；物体内能的增加量等于克服摩擦力所做的功，D正确．

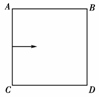
8．光滑水平面上有一边长为l的正方形区域处在场强为E的匀强电场中，电场方向与正方形一边平行，一质量为m、带电荷量为q的小球由某一边的中点，以垂直于该边的水平初速v₀进入该正方形区域．当小球再次运动到该正方形区域的边缘时，具有的动能可能为

(　)

A．0　 　　　　　　　　　　　　　　　　　　　 B.mv₀²+qEl

C.mv₀²　 　　　　　　　　　　　　　　　　　 D.mv₀²+qEl

答案：ABC

解析：如图所示，如果电场方向是AB方向则电场力可以做正功，也可以做负功，做负功时有可能使其动能变为零，故选项A正确；如果电场的方向是AC方向，带电小球到达AB或CD时，电场力做功为qEl/2，故选项B可能是正确的；如果带电小球回到同一个边界上，即回到等势面上，电场力不做功，故选项C可能是正确的；D是无论如何也是不可能的．

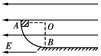
7．(2010·江门测试)x轴上有两点电荷Q₁和Q₂，Q₁和Q₂之间线上各点电势高低如图曲线所示(AP>PB)，选无穷远处电势为0，从图中可以看出(　)

A．Q₁电荷量一定小于Q₂电荷量

B．P点电场强度是0

C．Q₁和Q₂之间线上各点电场方向都指向Q₂

D．Q₁、Q₂可能是同种电荷

答案：C

解析：Q₁附近电势大于零，而Q₂附近电势小于零，可知Q₁带正电、Q₂带负电，D项错；Q₁、Q₂之间电场线由Q₁指向Q₂，C项正确；两电荷连线上P点场强一定不为零，B项错；由φ＝k知，Q₁在P点电势为φ＝k.Q₂在P点电势为φ₂＝－k，而P点电势为0，则有＝，r₁>r₂，故Q₁>Q₂，A项错．

6．如图所示，A、B是位于竖直平面内、半径R＝0.5 m的圆弧形的光滑绝缘轨道，其下端点B与水平绝缘轨道平滑连接，整个轨道处在水平向左的匀强电场中，电场强度E＝5×10³ N/C.今有一质量为m＝0.1 kg、带电荷量+q＝8×10^－5 C的小滑块(可视为质点)从A点由静止释放．若已知滑块与水平轨道间的动摩擦因数μ＝0.05，取g＝10 m/s²，求：

(1)小滑块第一次经过圆弧形轨道最低点B时B点的压力．

(2)小滑块在水平轨道上通过的总路程．

答案：(1)2.2 N　(2)6 m

解析：(1)设小滑块第一次到达B点时的速度为v_B，对圆弧轨道最低点B的压力为F，则：

mgR－qER＝mv_B²　F－mg＝m

故F＝3mg－2qE＝2.2 N

(2)由题意知小滑块最终将停在B点由动能定理得－F_f·S＝0－mv_B²结合F_f＝μmg可得小滑块在水平轨道上通过的总路程S＝6 m.

5．如图所示，小球的质量为m，带电荷量为q，悬挂小球的丝线与竖直方向成θ角时，小球恰好在匀强电场中静止不动，丝线长为L，现将小球拉到悬线竖直的方向上来，则静电力做功多少？拉力至少要做多少功？

答案：－qELsin θ　qELsin θ－mg(1－cos θ)

解析：小球受力如图，将小球拉到竖直位置时，静电力做功：

W_电＝－qEd＝－qElsin θ①

又由动能定理得：

W+W_电+W_G＝mv²－0②

要使W最小，只要让v＝0③

即缓慢拉到竖直位置，该过程，重力做功

W_G＝mgL(1－cos θ)④

由①②③④得W＝qELsin θ－mg(1－cos θ)．

4．将一正电荷从无限远处移入电场中M点，静电力做功W₁＝6×10^－9 J，若将一个等量的负电荷从电场中N点移向无限远处，静电力做功W₂＝7×10^－9 J，则M、N两点的电势φ_M、φ_N，有如下关系(　)

A．φ_M<φ_N<0　 　　　　　　　　　　　　　 B．φ_N>φ_M>0

C．φ_N<φ_M<0　 　　　　　　　　　　　　　 D．φ_M>φ_N>0

答案：C

解析：对正电荷φ_∞－φ_M＝；对负电荷φ_N－φ_∞＝，即φ_∞－φ_N＝.而W₂>W₁，φ_∞＝0，且和均大于0，则φ_N<φ_M<0，正确答案选C.

3．(2010·南通模拟)一质量为m的带电小球，在竖直方向的匀强电场中以水平速度抛出，小球的加速度大小为g，阻力不计，关于小球在下落h的过程中能量的变化，以下说法中正确的是(　)

A．动能增加了mgh　 　　　　　　　　　　 B．电势能增加了mgh

C．机械能减少了mgh　 　　　　　 D．重力势能减少了mgh

答案：BC

解析：由加速度可求出电场力大小为mg，方向竖直向上，小球在下落h的过程中，电场力做功W_电＝－mgh，电势能增加mgh；机械能减少mgh；合外力做功W_合＝mgh，动能增加mgh；重力势能减少mgh.

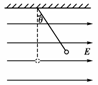
2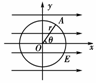．(2010·深圳调研)如图所示，在沿x轴正方向的匀强电场E中，有一质点A以O为圆心、以r为半径逆时针转动，当质点A转动至其与O点的连线与x轴正方向间夹角为θ时，则O、A两点间的电势差为(　)

A．U_OA＝Er　 　　　　　　　　　　　　　 B．U_OA＝Ersin θ

C．U_OA＝Ercos θ　 　　　　　　　　　　 D．U_OA＝

答案：C

解析：在匀强电场中，两点间的电势差与场强的关系为U＝Ed，其中d为沿电场方向的两点间的距离，所以U_OA＝Ercos θ，故C正确．

1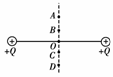．如图所示，在等量正点电荷连线的中垂线上取A、B、C、D四点，A、D两点与B、C两点均关于O点对称，令各点电势分别为φ_A、φ_B、φ_C、φ_D，则下列说法正确的是(　)

A．φ_A＝φ_B＝φ_C＝φ_D　 　　　　　　　 B．φ_A<φ_B、φ_D>φ_C

C．φ_A＝φ_D、φ_B＝φ_C　 　　　　　　　 D．φ_A>φ_C、φ_B>φ_D

答案：BC

解析：等量正点电荷连线的中点O处合场强为0，中垂线上O点上方合场强沿中垂线向上，下方合场强沿中垂线向下．由“沿场强方向电势降低”可判定A错误，B正确；电势是标量，由对称性知C正确，D错误．本题还可以根据等量正电荷等势面的分布情况，结合等势面与电场线的关系判断．

20．(12分)一平行板电容器长l＝10 cm，宽a＝8 cm，板间距d＝4 cm，在板左侧有一足够长的“狭缝”离子源，沿着两板中心平面，连续不断地向整个电容器射入离子，它们的均为5×10^－11 kg/C，速度均为4×10⁶ m/s，距板右端处有一屏，如图甲所示，如果在平行板电容器的两极板间接上如图乙所示的交流电，由于离子在电容器中运动所用的时间远小于交流电的周期，故离子通过电场的时间内电场可视为匀强电场．试求：

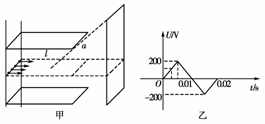
(1)离子打在屏上的区域面积；

(2)在一个周期内，离子打到屏上的时间．

答案：(1)4ad　(2)0.007 2 s

解析：(1)设离子恰好从极板边缘射出时的电压为U₀

水平方向：l＝v₀t①

竖直方向：＝at²②

又a＝③

由①②③得

U₀＝＝ V

＝128 V

当U≥128 V时打到极板上

当U<128 V时打到屏上

利用推论：打到屏的离子好像是从极板中心沿直线射到屏上．

由此可得＝

解得打到屏上的长度为y＝d

又由对称知，总长度为2d

区域面积为S＝2y·a＝4ad.

(2)在前T，离子打到屏上的时间

t₀＝×0.005 s＝0.001 8 s

又由对称性知，在一个周期内，打到屏上的总时间

t＝4t₀＝0.007 2 s.