1．做简谐振动的单摆，在摆动的过程中(　)

A．只有在平衡位置时，回复力才等于重力和细绳拉力的合力

B．只有在最高点时，回复力才等于重力和细绳拉力的合力

C．小球在任意位置处，回复力都等于重力和细绳拉力的合力

D．小球在任意位置处，回复力都不等于重力和细绳拉力的合力

解析：单摆在一个圆弧上来回运动，摆球做圆周运动的向心力由重力沿悬线方向的分力和悬线拉力的合力提拱，而回复力是指重力沿圆弧切线方向的分力．摆球在平衡位置速度不为零，向心力不为零，而回复力为零，所以合力不是回复力；摆球在最高点时，速度为零，向心力为零，合力等于回复力．故选项B正确．

答案：B

13．(2010·课标全国)如图所示，在0≤x≤a、0≤y≤范围内有垂直于xy平面向外的匀强磁场，磁感应强度大小为B，坐标原点O处有一个粒子源，在某时刻发射大量质量为m、电荷量为q的带正电粒子，它们的速度大小相同，速度方向均在xy平面内，与y轴正方向的夹角分布在0-90°范围内．已知粒子在磁场中做圆周运动的半径介于a/2到a之间，从发射粒子到粒子全部离开磁场经历的时间恰好为粒子在磁场中做圆周运动周期的四分之一．求最后离开磁场的粒子从粒子源射出时的

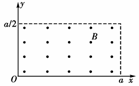
(1)速度的大小；

(2)速度方向与y轴正方向夹角的正弦．

答案：(1)　(2)sin α＝

解析：此题为粒子在磁场中运动临界值问题．

(1)设粒子的发射速度为v，粒子做圆周运动的轨道半径为R，由牛顿第二定律和洛伦兹力公式，得

qvB＝m①

由①式得R＝②

当a/2<R<a时，在磁场中运动时间最长的粒子，其轨迹是圆心为C的圆弧，圆弧与磁场的上边界相切，如图所示，设该粒子在磁场中运动的时间为t，依题意t＝T/4，得

∠OCA＝③

设最后离开磁场的粒子的发射方向与y轴正方向的夹角为α，由几何关系可得

Rsin α＝R－④

Rsin α＝a－Rcos α⑤

又sin²α+cos²α＝1⑥

由④⑤⑥式得

R＝a⑦

由②⑦式得

v＝⑧

(2)由④⑦式得

sin α＝

12．(2010·江苏单科)如图所示，在匀强磁场中附加另一匀强磁场，附加磁场位于图中阴影区域，附加磁场区域的对称轴OO′与SS′垂直．a、b、c三个质子先后从S点沿垂直于磁场的方向射入磁场，它们的速度大小相等，b的速度方向与SS′垂直，a、c的速度方向与b的速度方向间的夹角分别为α、β，且α>β.三个质子经过附加磁场区域后能到达同一点S′，则下列说法中正确的有(　)

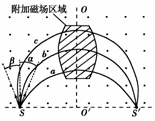
A．三个质子从S运动到S′的时间相等

B．三个质子在附加磁场以外区域运动时，运动轨迹的圆心均在OO′轴上

C．若撤去附加磁场，a到达SS′连线上的位置距S点最近

D．附加磁场方向与原磁场方向相同

答案：CD

解析：带电粒子在磁场中的回旋时间与回旋角成正比．由图知φ_c>φ_b>φ_a，可知t_c>t_b>t_a，A选项错误；三个质子在匀强磁场中轨道半径相等，即S到圆心的距离相等，所以三个圆心不可能都出现在OO′轴上，B项错误；若撤去附加磁场后，b质子经半圆打在SS′连线最远，a质子初速度方向与SS′线夹角最小，落点最近，故C项正确；圆心都在弧线一侧，所以附加磁场与原磁场方向相同，D项正确．

11．(2010·重庆理综)如图所示，矩形MNPQ区域内有方向垂直于纸面的匀强磁场，有5个带电粒子从图中箭头所示位置垂直于磁场边界进入磁场，在纸面内做匀速圆周运动，运动轨迹为相应的圆弧，这些粒子的质量、电荷量以及速度大小如下表所示.

由以上信息可知，从图中a、b、c处进入的粒子对应表中的编号分别为(　)

A．3、5、4　 　　　　　　　　　　　　　 B．4、2、5　

C．5、3、2　 　　　　　　　 　　　　　　　 D．2、4、5

答案：D

解析：结合题图，运用左手定则可知，粒子a与b电性相同，粒子c与前两者电性必相反，r_a＝r_c＝r_b，根据r＝可知，A项中r_a＝r_b，B项中r_a＝r_b，均与题意不符，A、B两项均错误．C项中若只剩粒子1和4则二者电性与图中其余两条轨道不符，故C项错误，只有D项符合，答案为D.

10．如图所示，一个质量为m、电荷量为e的静止质子，经电压为U的电场加速后，射入与其运动方向一致的磁感应强度为B的匀强磁场区域MN内，在MN内，有n块互成直角、长为L的硬质塑料板(不导电，宽度很窄，厚度不计，质子与塑料板作用前后的速度关系符合光的反射定律)．

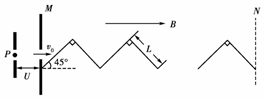
(1)求质子进入磁场时的速度v₀；

(2)若质子进入磁场后与每块塑料板碰撞时均没有能量损失，求质子穿过磁场区域所需的时间．

答案：(1)　(2)+

解析：(1)根据能的转化和守恒定律，

有eU＝mv₀²，得v₀＝

(2)质子打到第一块板上后反弹速度与原速度方向垂直，由于没有能量损失，以大小仍为v₀的速度垂直于磁场方向运动，显然，质子将以半径R在垂直于磁场的平面内做匀速圆周运动，转动一周后打到第一块板的下侧面，由于不计板的厚度，所以质子以第一次打到板和第二次打到板的时间间隔为质子在磁场中运动一周的时间，即一个周期T.

根据牛顿定律ev₀B＝和T＝，得T＝

质子在磁场中共碰到n块板，做圆周运动所需的时间为t₂＝nT

质子进入磁场中，在沿磁场方向做匀速直线运动时，总位移为s＝nLcos 45°，时间为t₁＝，

则t＝t₁+t₂＝+

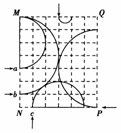
9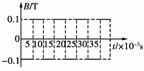．(2010·浙江金华)真空区域中存在如图所示形式变化的均匀磁场，该磁场的磁感应强度大小不变、方向随时间做周期性变化．一电荷量q＝5π×10^－7 C，质量m＝5×10^－10 kg的带电粒子，位于该真空区域中某点处，在t＝0时刻以初速度v₀＝π m/s沿垂直于磁场的方向开始运动．不计粒子重力的作用，不计磁场的变化可能产生的一切其他影响，则带电粒子在磁场中运动N个(N为整数)周期的时间内的平均速度的大小等于(　)

A．π m/s　　　　　　　　　　　　　　　　　　 B. m/s　

C．2 m/s　　 　　　　　　　　　　 D. m/s

答案：C

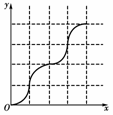解析：带电粒子在磁场中做圆周运动的半径为r＝＝0.01 m，周期为T＝＝0.02 s，则T/4＝0.005 s＝5×10^－3 s，对应磁场磁感应强度随时间的变化规律可知此段时间内磁感应强度不变，粒子恰好完成个圆周运动，……，做出粒子的轨迹示意图如图所示，所以带电粒子在磁场中运动N个(N为整数)周期的时间内的平均速度的大小＝＝2 m/s，C正确．

8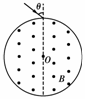．如图是某粒子速度选择器的示意图，在一半径为R＝10 cm的圆柱形桶内有B＝10^－4 T的匀强磁场，方向平行于轴线，在圆柱桶某一直径的两端开有小孔，作为入射孔和出射孔，粒子束以不同角度入射，最后有不同速度的粒子束射出．现有一粒子源发射比荷为＝2×10¹¹ C/kg的阳离子，粒子束中速度分布连续．当角θ＝45°时，出射粒子速度v的大小是(　)

A.×10⁶ m/s　 　　　　　　　　　　　　 B．2×10⁶ m/s

C．2×10⁸ m/s　 　　　　　　　　　　 D．4×10⁶ m/s

答案：B

解析：由题意，粒子从入射孔以45°角射入匀强磁场，粒子在匀强磁场中做匀速圆周运动，能够从出射孔射出的粒子刚好在磁场中运动周期，由几何关系知r＝R，

又r＝，v＝＝2×10⁶ m/s

7．(2010·三亚模拟)如图所示，在屏MN的上方有磁感应强度B的匀强磁场，磁场方向垂直纸面向里，P为屏上的一个小孔，PC与MN垂直．一群质量为m、带电荷量为－q的粒子(不计重力)，以相同的速率v，从P处沿垂直于磁场的方向射入磁场区域，粒子入射方向在与磁场B垂直的平面内，且散开在与PC夹角为θ的范围内，则在屏MN上被粒子打中的区域的长度为(　)

A.　 　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　 D.

答案：D

解析：粒子沿PC方向射入，偏转半个圆周打在MN上，长度l₁＝2R＝，

粒子沿与PC夹角为θ的方向射入，打在PN上的长度l₂＝，

则在屏MN上被粒子打中区域的长度

Δl＝l₁－l₂＝

6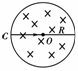．如图所示，直径为R的绝缘筒中为匀强磁场区域，磁感应强度为B、磁感线垂直纸面向里一个质量为m、电荷量为q的正离子，以速度v从圆筒上C孔处沿直径方向射入筒内，如果离子与圆筒碰撞三次(碰撞时不损失能量，且时间不计)，又从C孔飞出，则离子在磁场中运动的时间为(　)

A．2πR/v　 　　　　　　　　　　　　　　 B．πR/v 　

C．2πm/qB　　　　　　　　　　　　　 D．πm/qB

答案：AC

解析：根据对称性画出离子的运动轨迹应为三个1/3圆，半径等于圆筒的半径，总时间应等于一个圆周的周期，所以选项A、C正确．

5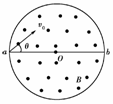．在真空中，半径r＝3×10^－2m的圆形区域内有匀强磁场，方向如图所示，磁感强度B＝0.2 T，一个带正电的粒子，以初速度v₀＝10⁶m/s从磁场边界上直径ab的一端a射入磁场，已知该粒子的比荷＝10⁸ C/kg，不计粒子重力．

求：(1)粒子在磁场中做匀速圆周运动的半径是多少？

(2)若要使粒子飞离磁场时有最大偏转角，求入射时v₀方向与ab的夹角θ及粒子的最大偏转角β.

答案：(1)5×10^－2 m　(2)37°　74°

解析：(1)粒子射入磁场后，由于不计重力，所以洛伦兹力充当圆周运动需要的向心力，根据牛顿第二定律有：

qv₀B＝

∴ R＝＝5×10^－2m.

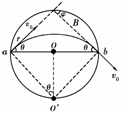
(2)粒子在圆形磁场区域轨迹为一段半径R＝5 cm的圆弧，要使偏转角最大，就要求这段圆弧对应的弦最长，即为场区的直径，粒子运动轨迹的圆心O′在ab弦中垂线上，如图所示：由几何关系可知：

sin θ＝＝0.6，∴ θ＝37°

而最大偏转角β＝2θ＝74°