
题目列表(包括答案和解析)
8.如图,-玩具车携带若干质量为m1的弹丸,车和弹丸的总质量为m2,在半径为R的水平光滑轨道上以速率V0做匀速圆周运动,若小车每一周便沿运动方向相对地面以恒定速度u发射-枚弹丸.求:
(1)至少发射多少颗弹丸后小车开始反向运动?
(2)写出小车反向运动前发射相邻两枚弹丸的时间间隔的表达式.

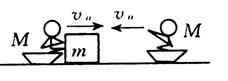
7.甲、乙两个小孩各乘一辆冰车在水平冰面上游戏,甲和他的冰车总质量共为M =30 kg,乙和他的冰车总质量也是30 kg,游戏时,甲推着一个质量m =15 kg的箱子,和他一起以大小为V0=2m/s的速度滑行,乙以同样大小的速度迎面滑来,如图,为了避免相撞,甲突然将箱子沿冰面推给乙,箱子滑到乙处时乙迅速把它抓住,若不计冰面的摩擦,问甲至少要以多大的速度(相对地面)将箱子推出,才能避免与乙相撞.(注意两人避免相撞的条件)
6.两块厚度相同的木块A和B,紧靠着放在光滑的水平面上,其质量分别为mA=2.0kg,mB=0.90kg,它们的下底面光滑,上表面粗糙,另有一质量mC=0.10kg的滑块C(可视为质点),以VC=10m/s的速度恰好水平地滑A的上表面,如图所示,由于摩擦,滑块最后停在木块B上,B和C的共同速度为0.50m/s.
(1)木块A的最终速度VA;
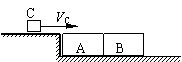 (2)滑块C离开A时的速度VC’
(2)滑块C离开A时的速度VC’
5.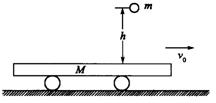 如图所示,质量为M的平板车在光滑水平面上以速度v匀速运动,车身足够长,其上表面粗糙,质量为m的小球自高h处由静止下落,与平板车碰撞后,每次上升高度仍为h,每次碰撞过程中,由于摩擦力的冲量不能忽略,小球水平速度逐渐增大,撞击若干次后,小球水平速度不再增大,则平板车的最终速度V是多大?
如图所示,质量为M的平板车在光滑水平面上以速度v匀速运动,车身足够长,其上表面粗糙,质量为m的小球自高h处由静止下落,与平板车碰撞后,每次上升高度仍为h,每次碰撞过程中,由于摩擦力的冲量不能忽略,小球水平速度逐渐增大,撞击若干次后,小球水平速度不再增大,则平板车的最终速度V是多大?
4.在质量为M 的小车中挂有一单摆,摆球的质量为m。,小车(和单摆)以恒定的速度V沿光滑水平地面运动,与位于正对面的质量为m的静止木块发生碰撞,碰撞时间极短,在此碰撞过程中,下列哪些说法是可能发生的( ).
A.小车、木块、摆球的速度都发生变化,分别变为V1、V2、V3,满足(m。十M)V=MVl十mV2十m。V3
B.摆球的速度不变,小车和木块的速度变为V1、V2,满足MV=MVl十mV2
C.摆球的速度不变,小车和木块的速度都变为V’,满足MV=(M 十m)V’
D.小车和摆球的速度都变为V1,木块的速度变为V2,满足(M+mo)V=(M+mo)Vl+mV2
3.一小型宇宙飞船在高空绕地球做匀速圆周运动如果飞船沿其速度相反的方向弹射出一个质量较大的物体,则下列说法中正确的是( ).
A.物体与飞船都可按原轨道运行
B.物体与飞船都不可能按原轨道运行
C.物体运行的轨道半径无论怎样变化,飞船运行的轨道半径一定增加
D.物体可能沿地球半径方向竖直下落
2.两名质量相等的滑冰人甲和乙都静止在光滑的水平冰面上.现在其中一人向另一人抛出一个篮球,另一人接球后再抛回.如此反复进行几次后,甲和乙最后的速率关系是 ( ).
A.若甲先抛球,则一定是V甲>V乙
B.若乙最后接球,则一定是V甲>V乙
C.只有甲先抛球,乙最后接球,才有V甲>V乙
D.无论怎样抛球和接球,都是V甲>V乙
1.质量为m的人随平板车以速度V在平直跑道上匀速前进,不考虑摩擦阻力,当此人相对于车竖直跳起至落回原起跳位置的过程中,平板车的速度 ( )
A.保持不变 B.变大 C.变小
D.先变大后变小 E.先变小后变大
5.如图所示,人与冰车质量为M,球质量为m,开始均静止于光滑冰面上,现人将球以对地速度V水平向右推出,球与挡板P碰撞后等速率弹回,人接住球后又将球以同样的速度V向右推出……如此反复,已知M = 16 m,试问人推球几次后将接不到球?
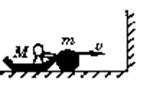
分析:(该题是多过程动量守恒问题,可以采用数学归纳的方法研究;当然也可整个过程采用动量定理研究)
解析: 取水平向左为正方向,冰车、人、球为系统.由动量守恒定律,
对第一次推球过程有: 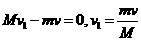
对第二次整个接、推球过程有: 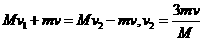
对第三次整个接、推球过程有:
对第n次整个接、推球过程同理分析得: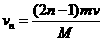
设推球n次后恰接不到球,则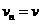 ,故有
,故有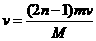 代人已知条件
代人已知条件
解得:n = 8.5, 即人推球9次后将接不到球.
三:动量守恒定律适应练习
丹阳六中 马跃中
4.如图所示,一块足够长的木板,放在光滑水平面上,在木板上自左向右并非放有序号是1,2,3,…,n的物体,所有物块的质量均为m,与木板间的动摩擦因数都相同,开始时,木板静止不动,第1,2,3,…n号物块的初速度分别是v ,2 v
,2 v ,3 v
,3 v ,…nv
,…nv ,方向都向右,木板的质量与所有物块的总质量相等 ,最终所有物块与木板以共同速度匀速运动。设物块之间均无相互碰撞,木板足够长。试求:
,方向都向右,木板的质量与所有物块的总质量相等 ,最终所有物块与木板以共同速度匀速运动。设物块之间均无相互碰撞,木板足够长。试求:
(1)所有物块与木板一起匀速运动的速度v ;
;
(2)第1号物块与木板刚好相对静止时的速度v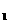 ;
;
(3)通过分析与计算说明第k号(k<n=物块的最小速度v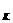

分析:(多个物体组成的系统,应恰当选择小系统利用动量守恒定律求解)
在木板上各个物块相对木板运动,都给木板一个向右的磨擦力,因各个物块质量相同,滑动磨擦力都一样,木板在磨擦力的作用下向右加速。由于每个物块的初始速度不同,因而相对木板静止的物块顺序依次是1,2,…,n号,当第一号物块由v 到相对木板静止时,其动量变化设为△p
到相对木板静止时,其动量变化设为△p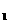 ,则其他各个所有物块在这段时间内的动量变化也都为△p
,则其他各个所有物块在这段时间内的动量变化也都为△p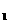 (f相同,T相同),因木板与所有物块总动量守恒,故可用动量守恒关系求出第1号物块相对木板静止时的速度。
(f相同,T相同),因木板与所有物块总动量守恒,故可用动量守恒关系求出第1号物块相对木板静止时的速度。
解析:(1)设所有物块都相对木板静止时的速度为 v ,因木板与所有物块系统水平方向不受外力,动量守恒,应有:
,因木板与所有物块系统水平方向不受外力,动量守恒,应有:
m v +m·2 v
+m·2 v +m·3 v
+m·3 v +…+m·n v
+…+m·n v =(M + nm)v
=(M + nm)v 1
1
M = nm, 2
解得:
v =
=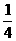 (n+1)v
(n+1)v ,
,
(2)设第1号物块相对木板静止时的速度为v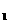 ,取木板与物块1为系统一部分,第2 号物块到第n号物块为系统另一部分,则
,取木板与物块1为系统一部分,第2 号物块到第n号物块为系统另一部分,则
木板和物块1 △p =(M + m)v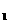 -m v
-m v ,
,
2至n号物块 △p =(n-1)m·(v
=(n-1)m·(v - v
- v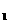 )
)
由动量守恒定律: △p=△p ,
,
解得
v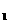 =
=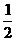 v
v ,
3
,
3
(3)设第k号物块相对木板静止时的速度由v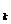 ,则第k号物块速度由k
v
,则第k号物块速度由k
v 减为v
减为v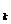 的过程中,序数在第k号物块后面的所有物块动量都减小m(k v
的过程中,序数在第k号物块后面的所有物块动量都减小m(k v - v
- v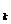 ),取木板与序号为1至K号以前的各物块为一部分,则
),取木板与序号为1至K号以前的各物块为一部分,则
△p=(M+km)v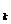 -(m v
-(m v +m·2 v
+m·2 v +…+mk v
+…+mk v )=(n+k)m v
)=(n+k)m v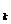 -
-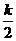 (k+1)m v
(k+1)m v
序号在第k以后的所有物块动量减少的总量为
△p =(n-k)m(k v
=(n-k)m(k v - v
- v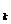 )
)
由动量守恒得 △p=△p , 即
, 即
(n+k)m v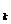 -
-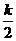 (k+1)m v
(k+1)m v = (n-k)m(k v
= (n-k)m(k v - v
- v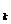 ),
),
解得 v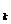 =
=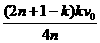
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com