
题目列表(包括答案和解析)
2.受力分析的思路和步骤
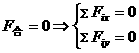
|
板块 |
重要“知识背景” |
疑难问题 |
典型问题 |
|
受力分析 |
1. 静摩擦力与滑动摩擦力 弹力与作用力 2. 图2-5-3(a)中的AC、BD两杆均以角速度 t=0时,
向心加速度的大小恒为
再看图2-5-4(a),一平面内有二根细杆 参考图2-5-4(b),经过时间
因为
因此两杆交点相对于纸平面的速度
不难看出,经过
=
用同样的方法可以求出交点相对
因为 如果 2.5.1、相关的速度
如图2-5-1所示的情况,绳AB拉 分速度vsina和水平分速度vcosa,以为木块的速度 如图2-5-2所示,杆AB沿滑下,A、B二端的速度
10.解:(1)小球
解得: (2)当球 水平方向动量守恒有 根据能量关系 解得: 9.解:(1)物体在两斜面上来回运动时,克服摩擦力所做的功 物体从开始直到不再在斜面上运动的过程中
解得 (2)物体最终是在 (3)物体第一次通过圆弧最低点时,圆弧所受压力最大.由动能定理得
由牛顿第二定律得 解得 物体最终在圆弧上运动时,圆弧所受压力最小.由动能定理得
由牛顿第二定律得 解得 8.解:(1)由机械能守恒 得: (2)在最低点 得: 7.解:由于滑动摩擦力
所以物体最终必定停在P点处,由功能关系有
6.解:⑴物块在光滑轨道上滑动过程机械能守恒,第一次下滑到底端
由于每次与档板碰后速度大小都是碰前的
由①、②得 ⑵物块第二次与档板碰后沿圆形轨道上升的最大高度 第二次与档板碰后速度: 则第二次与档板碰撞到第三次与档板碰撞间隔的时间为:
第三次与档板碰后速度: 则第三次与档板碰撞到第四次与档板碰撞间隔的时间为:
因此第二次与档板碰撞到第四次与档板碰撞间隔的时间为:
5.(略) 同步练习册答案 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。 ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号 |