
题目列表(包括答案和解析)
3.实物电路连接时按一定顺序并注意规范要求(参照附录)
例2.从下表中选出适当的器材,设计一个电路,来测量A1的电阻r1,要求方法简捷,有尽可能高的测量精度,并测得多组数据。
|
器
材 |
规
格 |
|
电流表A1 电流表A2 电压表(V) 电阻R1 滑动变阻器(R2) 电池(E) 电键K 导线若干 |
量程10mA内阻r1待测(约40Ω) 量程500μA内阻r2=750Ω 量程10V内阻r3=10kΩ 阻值约100Ω保护电阻 总阻值约50Ω 电动势1.5V,内阻很小 |
(1) 画出电路图,标明所选用器材的符号。
(2) 若选测量数据中的一组来计算,所选用的表达式为r1=___________,式中各符号的物理定义是:___________。
[析与解]由于本题要求测电流表内阻,给出的器材中又有电压表和电流表,首先联想到伏安法测电阻。由于待测电流表A1的量程I1=10mA。,内阻r1约为40Ω,则电流表A1两端的最大电压为U1m=I1m r1=10×10-3×40V=0.4V。若用量程为10V的电压表与电流表A1并联测电压,电压表读数误差太大,不符合精确性原则的要求,此电压表不能选用。既不能直接用伏安法测电流A1的电阻。
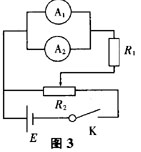 注意到电流表A2的内阻r2=750Ω为已知,实验中流过电流表A1和电流表A2电流又可以读出,就可以想到用分流关系来测量电流表A1的电阻。再看电流表A2两端的最大电压为U2m=I2m r2=500×10-6×750V=0.375V,并联使用时两电流表的读数符合准确性原则。这样就可以用I1 r1=I2 r2,即r1= I2 r2/I1来计算电流表A1的电阻。
注意到电流表A2的内阻r2=750Ω为已知,实验中流过电流表A1和电流表A2电流又可以读出,就可以想到用分流关系来测量电流表A1的电阻。再看电流表A2两端的最大电压为U2m=I2m r2=500×10-6×750V=0.375V,并联使用时两电流表的读数符合准确性原则。这样就可以用I1 r1=I2 r2,即r1= I2 r2/I1来计算电流表A1的电阻。
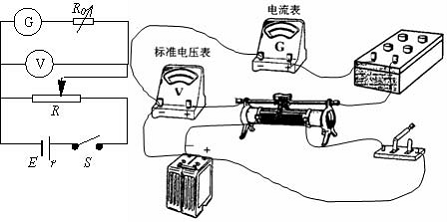
另外根据实验的其他要求连成如图所示电路。
[小结]1.通常在确定实验的原理时,可把给定的器材能够测量出的物理量看作已知量,再加上题目直接给出已知量,把要测定的物理量看作末知量,这样就可以看成一个同学们熟悉计算题。就可以把此题的结论作为测量的原理。这是设计性实验原理确定的又一途径。
 例1、将满偏电流Ig=300μA、内阻未知的电流表
例1、将满偏电流Ig=300μA、内阻未知的电流表
 改装成电压表并进行核对.
改装成电压表并进行核对.
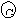 (1)利用如图所示的电路测量电流表 的内阻(图中电源的电动势E=4V )
:先闭合S1,调节R,使电流表指针偏转到满刻度;再闭合S2,保持R 不变,调节R′,使电流表指针偏转到满刻度的2/3,读出此时R′的阻值为200Ω,则电流表内阻的测量值Rg= Ω。
(1)利用如图所示的电路测量电流表 的内阻(图中电源的电动势E=4V )
:先闭合S1,调节R,使电流表指针偏转到满刻度;再闭合S2,保持R 不变,调节R′,使电流表指针偏转到满刻度的2/3,读出此时R′的阻值为200Ω,则电流表内阻的测量值Rg= Ω。
(2)将该表改装成量程为3V 的电压表,需 (填“串联”或“并联”)阻值为R0= Ω的电阻。
(3)把改装好的电压表与标准电压表进行核对,试在答题卡上画出实验电路图和实物连
接图。
[析与解]此题虽然不是半偏法,但与半偏法的原理相似,电流表指针为2/3,说明流过R′的电流是1/3,因此由并联电路的分流关系可得电流表的电阻为R′的电阻的一半。电流表改装成电压表时应串联一个分压电阻R分=(U-Ig*Rg) /Ig=9900Ω。改装后的电压表在校表时应把滑动变阻器接成分压式接法。
[答案](1)100 (2)串联 9900 (3)
[小结]1.本题属设计性实验,它用到的原理和电路的选择均源于学生实验。考题中的设计性实验涉及到的原理和实验的方法也多源于课本。因此在进行实验复习时把重点放在实验的原理和实验方法及仪器的操作和读数上。在进行实验设计时,先根据题目要求和给出的条件,回顾分组实验和演示实验,寻找能够迁移应用的实验原理。依据类似的实验确定实验原理和方法。这是解决设计性实验的主要渠道。
2.滑动变阻器的接法在以下三种情况下必须采用分压式接法:①要求被测部分电压变化范围尽可能大(或从零调起) ②电压表或电流表量程不够 ③变阻器电阻远小于被测电阻。
实验设计过程可用下面的框图表示
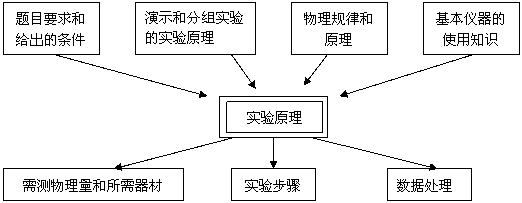
解决设计型实验问题的关键是确定实验原理,它是进行实验设计的根本依据和起点,它决定应当测量那些物理量、如何安排实验步骤、如何处理数据等。实验原理的确定,要根据问题的要求和给出的条件,回顾分组实验和演示实验,寻找能够迁移应用的实验原理,或者回顾物理原理,寻找有关的物理规律,设法创设相关的物理情景,并根据已掌握的基本仪器核对是否能够测出必须测定的物理量。因此,掌握基本仪器的使用方法、基本的实验方法和基本物理原理是解答设计型实验题的基础。
(1)合理性原则::实验方案所依据的原理应当符合物理学的基本原理,实验装置或电路能够圆满完成实验的要求。
(2)安全性原则:实验进行的过程中不会对实验装置和器材造成损坏,不会对人身造成危害。如每个电路元件上的电流、电压、电功率不超过元件的额定值,电源的电流不能超过电源允许输出的最大电流,电压表、电流表不能超过其量程。
(3)准确性原则:根据实验的需要,选用精度合适的测量工具,但对某个实验来讲,精确程度够用即可,并不是精度越高越好。对各种电表,一般要求它的实际读数不小于量程的2/3,使用欧姆表进尽可能使指针在中心刻度附近;为减少测量的影响,应选择内阻较小的电流表和内阻较大的电压表。
(4)方便性原则:实验时需考虑调节方便,便于操作,如滑动变阻器的选择,既要考虑它的额定电流,又要考虑它有阻值范围,在二者都能满足实验要求的情况下,还要考虑阻值大小对实验操作中是否调节方便的影响。
设计性物理实验,是依据课本中已经出现过的物理实验的基本原理、所使用的基本器材、以及在这些实验中学过的有关方法等,根据提供有关的实验器材以及实验要求,去设计一些新的实验方案,并按照实验设计方案及要求,完成实验有关内容。
10、一辆汽车在十字路口等候绿灯,当绿灯亮时汽车以3m/s2的加速度开始行驶,恰在这时一辆自行车以6m/s的速度匀速驶来,从后边赶过汽车。试求:
(1) 汽车从路口开动后,在追上自行车之前经过多长时间两车相距最远?此时距离是多少?
(2) 什么时候汽车追上自行车,此时汽车的速度是多少?
解析:解法一:汽车开动后速度由零逐渐增大,而自行车的速度是定值。当汽车的速度还小于自行车速度时,两者的距离将越来越大,而一旦汽车速度增加到超过自行车速度时,两车距离就将缩小。因此两者速度相等时两车相距最大,有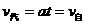 ,所以,
,所以,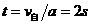
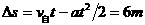
解法二:用数学求极值方法来求解
(1) 设汽车在追上自行车之前经过t时间两车相距最远,
因为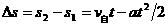
所以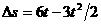 ,由二次函数求极值条件知,
,由二次函数求极值条件知,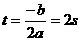 时,
时,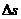 最大
最大
即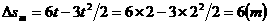
(2)汽车追上自行车时,二车位移相等,则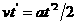
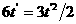 ,
, 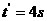
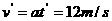
解法三:用相对运动求解更简捷
选匀速运动的自行车为参考系,则从运动开始到相距最远这段时间内,汽车相对此参考系的各个物理量为:
初速度v0 = v汽初-v自 =(0-6)m/s = -6m/s
末速度vt = v汽末-v自 =(6-6)m/s = 0
 加速度 a = a汽-a自 =(3-0)m/s2 = 3m/s2
加速度 a = a汽-a自 =(3-0)m/s2 = 3m/s2
所以相距最远 s=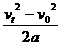 =-6m(负号表示汽车落后)
=-6m(负号表示汽车落后)
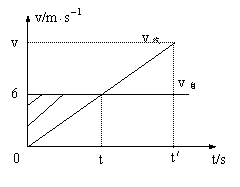
解法四:用图象求解
(1)自行车和汽车的v-t图如图,由于图线与横坐标轴所包围的面积表示位移的大小,所以由图上可以看出:在相遇之前,在t时刻两车速度相等时,自行车的位移(矩形面积)与汽车的位移(三角形面积)之差(即斜线部分)达最大,所以
t=v自/a=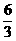 s=2s
s=2s
△s= vt-at2/2 =(6×2-3×22/2)m= 6m
(2)由图可看出:在t时刻以后,由v自或与v汽线组成的三角形面积与标有斜线的三角形面积相等时,两车的位移相等(即相遇)。所以由图得相遇时,t’= 2t = 4s,v’= 2v自=12m/s
答案 (1)2s 6m (2)12m/s
8、摩托车在平直公路上从静止开始起动,a1=1.6m/s2,稍后匀速运动,然后减速,a2=6.4m/s2,直到停止,共历时130s,行程1600m。试求:
(1) 摩托车行驶的最大速度vm;
(2) 若摩托车从静止起动,a1、a2不变,直到停止,行程不变,所需最短时间为多少?
分析:(1)整个运动过程分三个阶段:匀加速运动;匀速运动;匀减速运动。可借助v-t图象表示。
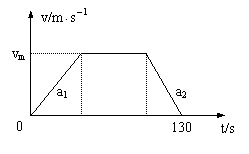 (2)首先要回答摩托车以什么样的方式运动可使得时间最短。借助v-t图象可以证明:当摩托车以a1匀加速运动,当速度达到v/m时,紧接着以a2匀减速运动直到停止时,行程不变,而时间最短
(2)首先要回答摩托车以什么样的方式运动可使得时间最短。借助v-t图象可以证明:当摩托车以a1匀加速运动,当速度达到v/m时,紧接着以a2匀减速运动直到停止时,行程不变,而时间最短
解:(1)如图所示,利用推论vt2-v02=2as有: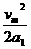 +(130-
+(130-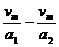 )vm+
)vm+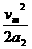
 =1600.其中a1=1.6m/s2,a2=6.4m/s2.解得:vm=12.8m/s(另一解舍去).
=1600.其中a1=1.6m/s2,a2=6.4m/s2.解得:vm=12.8m/s(另一解舍去).
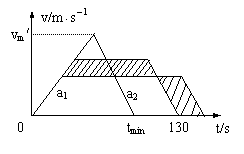 (2)路程不变,则图象中面积不变,当v越大则t越小,如图所示.设最短时间为tmin,则tmin=
(2)路程不变,则图象中面积不变,当v越大则t越小,如图所示.设最短时间为tmin,则tmin=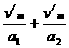 ①
①
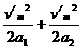 =1600 ②
=1600 ②
其中a1=1.6m/s2,a2=6.4m/s2.由②式解得vm=64m/s,故tmin=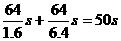 .既最短时间为50s.
.既最短时间为50s.
答案:(1)12.8m/s (2)50s
9一平直的传送以速率v=2m/s匀速行驶,传送带把A处的工件送到B处,A、B两处相距L=10m,从A处把工件无初速度地放到传送带上,经时间t=6s能传送到B处,欲使工件用最短时间从A处传送到B处,求传送带的运行速度至少应多大?
解析:物体在传送带上先作匀加速运动,当速度达到v=2m/s后与传送带保持相对静止,作匀速运动.设加速运动时间为t,加速度为a,则匀速运动的时间为(6-t)s,则:
v=at ①
s1=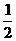 at2 ②
at2 ②
s2=v(6-t) ③
s1+s2=10 ④
联列以上四式,解得t=2s,a=1m/s2
物体运动到B处时速度即为皮带的最小速度
由v2=2as 得v=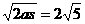 m/s
m/s
传送带给物体的滑动摩擦力提供加速度,即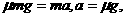 此加速度为物体运动的最大加速度.要使物体传送时间最短,应让物体始终作匀加速运动
此加速度为物体运动的最大加速度.要使物体传送时间最短,应让物体始终作匀加速运动
7、天文观测表明,几乎所有远处的恒星(或星系)都在以各自的速度背离我们而运动,离我们越远的星体,背离我们运动的速度(称为退行速度)越大;也就是说,宇宙在膨胀,不同星体的退行速度v和它们离我们的距离r成正比,即v=Hr。式中H为一常量,称为哈勃常数,已由天文观察测定,为解释上述现象,有人提供一种理论,认为宇宙是从一个大爆炸的火球开始形成的,假设大爆炸后各星体即以不同的速度向外匀速运动,并设想我们就位于其中心,则速度越大的星体现在离我们越远,这一结果与上述天文观测一致。
由上述理论和天文观测结果,可估算宇宙年龄T,其计算式如何?根据近期观测,哈勃常数H=3×10-2m/(s 光年),其中光年是光在一年中行进的距离,由此估算宇宙的年龄约为多少年?
解析:由题意可知,可以认为宇宙中的所有星系均从同一点同时向外做匀速直线运动,由于各自的速度不同,所以星系间的距离都在增大,以地球为参考系,所有星系以不同的速度均在匀速远离。则由s=vt可得r=vT,所以,宇宙年龄:T=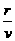 =
=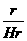 =
=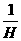
若哈勃常数H=3×10-2m/(s 光年)
则T=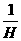 =1010年
=1010年
思考:1 宇宙爆炸过程动量守恒吗?如果爆炸点位于宇宙的“中心”,地球相对于这个“中心”做什么运动?其它星系相对于地球做什么运动?
2 其它星系相对于地球的速度与相对于这个“中心”的速度相等吗?
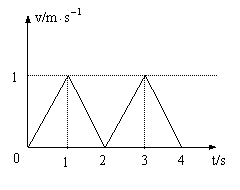
6、一物体在A、B两点的正中间由静止开始运动(设不会超越A、B),其加速度随时间变化如图所示。设向A的加速度为为正方向,若从出发开始计时,则物体的运动情况是( )
A 先向A ,后向B,再向A,又向B,4秒末静止在原处
B 先向A ,后向B,再向A,又向B,4秒末静止在偏向A的某点
 C 先向A ,后向B,再向A,又向B,4秒末静止在偏向B的某点
C 先向A ,后向B,再向A,又向B,4秒末静止在偏向B的某点
D 一直向A运动,4秒末静止在偏向A的某点
解析:根据a-t图象作出其v-t图象,如右图所示,由该图可以看出物体的速度时大时小,但方向始终不变,一直向A运动,又因v-t图象与t轴所围“面积”数值上等于物体在t时间内的位移大小,所以4秒末物体距A点为2米
答案:D
5、在轻绳的两端各栓一个小球,一人用手拿者上端的小球站在3层楼阳台上,放手后让小球自由下落,两小球相继落地的时间差为T,如果站在4层楼的阳台上,同样放手让小球自由下落,则两小球相继落地时间差将 ( )
A 不变 B 变大 C 变小 D 无法判断
解析:两小球都是自由落体运动,可在一v-t图象中作出速度随时间的关系曲线,如图所示,设人在3楼阳台上释放小球后,两球落地时间差为△t1,图中阴影部分面积为△h,若人在4楼阳台上释放小球后,两球落地时间差△t2,要保证阴影部分面积也是△h;从图中可以看出一定有△t2〈△t1
答案:C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com