
题目列表(包括答案和解析)
4. 平行板电容器的电容为C, 带电量为Q, 极板间的距离为d. 在两极板间的中点放一电量很小的点电荷q.它所受的电场力的大小等于 ( C )
A.8kQq/d2 B.4kQq/d2 C.Qq/Cd D.2Qq/Cd
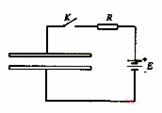 1.两块大小、形状完全相同的金属平板平行放置,构成一平行板电容器,与它相连接的电路如图所示,接通开关K,电源即给电容器充电. ( BC )
1.两块大小、形状完全相同的金属平板平行放置,构成一平行板电容器,与它相连接的电路如图所示,接通开关K,电源即给电容器充电. ( BC )
A.保持K接通,减小两极板间的距离,则两极
板间电场的电场强度减小
B.保持K接通,在两极板间插入一块介质,
则极板上的电量增大
C.断开K,减小两极板间的距离,
则两极板间的电势差减小
D.断开K,在两极板间插入一块介质,则两极板间的电势差增大
2.某电解电容器上标有“25V、470μF”的字样,对此,下列说法正确的是(A)
A、此电容器只能在直流25V及以下电压才能正常工作。
B、此电容器只能在交流25V及以下电压才能正常工作。
C、当工作电压是25V时,电容才是470μF。
D、这种电容器使用时,不必考虑两个引出线的极性。
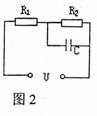 3.在图2的电路中,U=8V不变,电容器电容C=200
3.在图2的电路中,U=8V不变,电容器电容C=200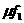 ,R1:R2=3:5,则电容器的带电量为 ( A
)
,R1:R2=3:5,则电容器的带电量为 ( A
)
A.1×10-3C
B.1.5×10-3C
C.6×10-4C
D.1.6×10-3C
例题1、如图所示,平行板电容器的两极板A、B接于电池两极,一带正电的小球悬挂在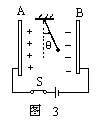 电容器内部,闭合S,电容器充电,这时悬线偏离竖直方向的夹角为θ.(AD)
电容器内部,闭合S,电容器充电,这时悬线偏离竖直方向的夹角为θ.(AD)
A.保持S闭合,将A板向B板靠近,则θ增大
B.保持S闭合,将A板向B板靠近,则θ不变
C.断开S,将A板向B板靠近,则θ增大
D.断开S,将A板向B板靠近,则θ不变
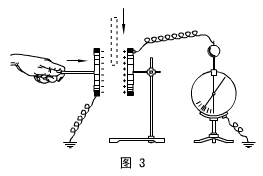 例题2、如图所示,让平行板电容器带电后,静电计的指针偏转一定角度,若不改变两极板带的电量而减小两极板间的距离,同时在两极板间插入电介质,那么静电计指针的偏转角度( A )
例题2、如图所示,让平行板电容器带电后,静电计的指针偏转一定角度,若不改变两极板带的电量而减小两极板间的距离,同时在两极板间插入电介质,那么静电计指针的偏转角度( A )
A、一定减小
B、一定增大
C、一定不变
D、可能不变
例题3、如图所示电路中,电源电动势ε=10V,内阻r=1Ω,电容器电容C1=C2=30μF,电阻R1=3Ω,R2=6Ω,开关K先闭合,待电路中电流稳定后再断开K,问断开开关K后,流过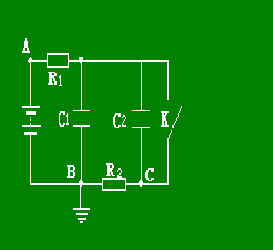 电阻R1的电量是多少?A、C两点的电势如何变化?
电阻R1的电量是多少?A、C两点的电势如何变化?
分析与解:我们从电路上看到,开关由闭合到断开,电容器上的电压发生变化,使电容器所带电量发生变化,这个变化要通过电容的充放电来实现,如果这个充放电电流要经过R1,那么我们就可以通过电容器带电量的变化来确定通过R1的电量。当K断开,稳定后,电路中没有电流,C1上板与A点等势,C点与B点等势,C1、C2两端电压均为电源电动势,所以
Q1'=C1ε=30×10-6×10=3.0×10-4库
Q2=C2ε=30×10-6×10 =3.0×10-4库且两电容带电均为上正下负
所以K断开后C1继续充电,充电量△Q1=Q1'-Q1=3.0×10-4-1.8×10-4-=1.2×10-4库
这些电荷连同C2所充电量都要通过R1, 故通过R1的电量Q=△Q1+Q2=1.2×10-4+3.0×10-4=4.2×10-4库
A点电势UA=10V, C点电势UC=0V,所以A点电势升高,C点电势降低.
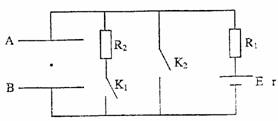
例题4、电源内阻r=2Ω,R1=8Ω,R2=10Ω,K1闭合,K2断开时,在相距d=70cm,水平放置的固定金属板AB间有一质量m=1.0g,带电量为q=7×10-5C的带负电的微粒,恰好静止在AB两板中央的位置上,求(1)电源的电动势(2)将K1断开0.1s后,又将K2闭合,微粒再经过多长时间与极板相碰。(g=10m/s2)
 [解答](1)
[解答](1)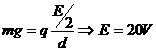 (4分)
(4分)
(2)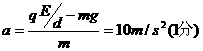
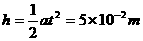 (1分)
(1分)
 (1分)
(1分)
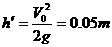 距上极板25cm时V=0粒子不能碰到上极板(2分)
距上极板25cm时V=0粒子不能碰到上极板(2分)
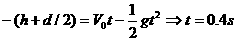 (2分)
(2分)
例题5、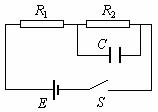 如图所示的电路中,电源电动势E=6.00V,其内阻可忽略不计.电阻的阻值分别为R1=2.4kΩ、R2=4.8kΩ,电容器的电容C=4.7μF.闭合开关S,待电流稳定后,用电压表测R1两端的电压,其稳定值为1.50V.
如图所示的电路中,电源电动势E=6.00V,其内阻可忽略不计.电阻的阻值分别为R1=2.4kΩ、R2=4.8kΩ,电容器的电容C=4.7μF.闭合开关S,待电流稳定后,用电压表测R1两端的电压,其稳定值为1.50V.
(1)该电压表的内阻为多大?
(2)由于电压表的接入,电容器的带电量变化了多少?
[解答]:(1)设电压表的内阻为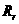 ,测得
,测得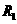 两端的电
压为
两端的电
压为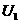 ,
,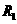 与
与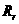 并联后的总电阻为R,则有
并联后的总电阻为R,则有
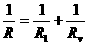 ①
①
由串联电路的规律
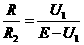 ②
②
联立①②,得
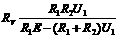
代人数据。得
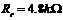
(2)电压表接入前,电容器上的电压 等于电阻
等于电阻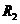 上的电压,
上的电压,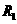 两端的电压为
两端的电压为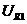 ,则
,则
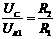
又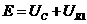
接入电压表后,电容器上的电压为 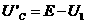
由于电压表的接入,电容器带电量增加了 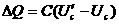
由以上各式解得 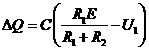
带入数据,可得 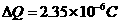
8.解析:(1)U形框向右运动时,NQ边相当于电源,产生的感应电动势E=Blv0,当如图乙所示位置时,方框bd之间的电阻为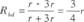
U形框连同方框构成的闭合电路的总电阻为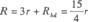
闭合电路的总电流为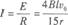
根据欧姆定律可知,bd两端的电势差为:Ubd=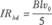
方框中的热功率为: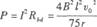
(2)在U形框向右运动的过程中,U形框和方框组成的系统所受外力为零,故系统动量守恒,设到达图示位置时具有共同的速度v,根据动量守恒定律
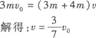
根据能量守恒定律,U形框和方框组成的系统损失的机械能等于在这一过程中两框架上产生的热量,即
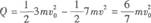
(3)设U形框和方框不再接触时方框速度为v1, u形框的速度为v2:,根据动量守恒定律,有3mv=4mvI+3mv2……两框架脱离以后分别以各自的速度做匀速运动,经过时间t方框最右侧和U形框最左侧距离为s,即(v2-v1)t=s联立以上两式,解得
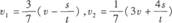
7.解析:(1)撤去F之前,设通过电阻R的电流为I,则金属杆受到的安培力大小F安=BIL=F.撤去F之后,由P=I2R知,当电阻R上消耗的电功率为P/4时,通过R的电流I'=I/2,则金属杆受到的安培力F’安=BI'L=F/2,方向水平向左,由牛顿第二定律得,
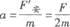 .方向水平向左.
.方向水平向左.
(2)撤去F后,金属杆在与速度方向相反的安培力作用下,做减速运动直到停下。设匀速运动时金属杆的速度为v,则I2(R+r)=Fv,又P=I2R,解得
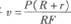
由能量守恒可得,撤去F后,整个电路产生的热量
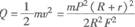
则电阻R上产生的焦耳热
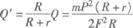
6.答案:4;0.28;0.08
解析:F安=(M-m)g,转化的内能=F安L
5.答案:0.5W
解析:由题意分析知,当砝码加速下落到速度最大时,砝码的合外力为零,此时R得到功率最大,为mg=BImaxL ①
Pmax=I2maxR②
由式①②得 Pmax=(mg/BL)2R=0.5W
4.答案:C
解析:这是一道选用力学规律求解电磁感应的好题目,线框做的是变加速运动,不能用运动学公式求解,那么就应想到动能定理,设线框刚进出时速度为v1和v2,则第一阶段产生的热量
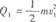
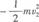
,第二阶段产生的热量Q2=mv2/2,只要能找出v1和v2的关系就能找到答案,由动量定理可得
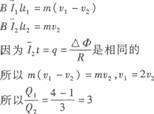
3.答案:D
解析:铝环向右运动时,环内感应电流的磁场与磁铁产生相互作用,使环做减速运动,磁铁向右做加速运动,待相对静止后,系统向右做匀速运动,由I=(m+M)v,得v=I/(m+M),即为磁铁的最大速度,环的最小速度,其动能的最小值为m/2·{I/(m+M)}2,铝环产生的最大热量应为系统机械能的最大损失量,I2/2m-I2/2(m+M)=MI2/2m(m+M).
2.答案:A
解析:两种情况下产生的总热量,都等于金属棒的初动能.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com