1.　　 如图所示是一位跳水运动员完成动作时头部的运动轨迹，最后运动员以速度v沿竖直方向入水，则在轨迹的a、b、c、d四个位置中，头部的速度方向也竖直的是

　A　 a位置　　　 B　 b位置　　 C　 c位置　　　 D　 d位置

[物体做曲线运动的条件]

[合运动和分运动]

28、宇航员在一星球表面上的某高处，沿水平方向抛出一小球。经过时间t，小球落到星球表面，测得抛出点与落地点之间的距离为L。若抛出时初速度增大到2倍，则抛出点与落地点之间的距离为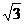L。已知两落地点在同一水平面上，该星球的半径为R，万有引力常数为G。求该星球的质量M。

分析与解：设抛出点的高度为h,第一次平抛的水平射程为x,则有

　　　　　　 x²+h²=L²　　　　

由平抛运动规律得知，当初速度增大到2倍时，其水平射程也增大到2x,可得　　　 (2x)²+h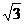²=(L)²　　　　　　　

设该星球上的重力加速度为g，由平抛运动的规律得：

　　　 h=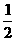gt²　　　　　　　　　　　　

由万有引力定律与牛顿第二定律得：

　 mg= G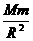　　　　　　　　　　　　　

联立以上各式解得M=。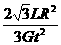

27、(2004年广西物理试题)某颗地球同步卫星正下方的地球表面上有一观察者，他用天文望远镜观察被太阳光照射的此卫星，试问，春分那天(太阳光直射赤道)在日落12小时内有多长时间该观察者看不见此卫星？已知地球半径为R，地球表面处的重力加速度为g,地球自转周期为T，不考虑大气对光的折射。

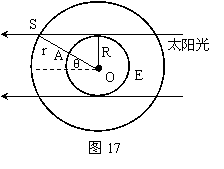分析与解：设所求的时间为t，用m、M分别表示卫星和地球的质量，r表示卫星到地心的距离.有

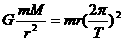
春分时，太阳光直射地球赤道，如图17所示，图中圆E表示赤道，S表示卫星，A表示观察者，O表示地心. 由图17可看出当卫星S绕地心O转到图示位置以后(设地球自转是沿图中逆时针方向)，其正下方的观察者将看不见它. 据此再考虑到对称性，有

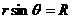
由以上各式可解得　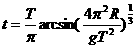 例26、某卫星沿椭圆轨道绕行星运行，近地点离行星中心的距离是a,远地点离行星中心的距离为b,若卫星在近地点的速率为V_a,则卫星在远地点时的速率V_b多少？

分析:椭圆运动的卫星在近地点和远地点的轨道曲率半径相同，设都等于R。所以，在近地点时有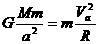，在远地点时有，上述两式相比得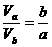，故。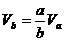

26、行星的平均密度是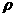，靠近行星表面的卫星运转周期是T，试证明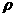：T²是一个常量，即对任何行星都相同。

证明：因为行星的质量M=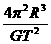(R是行星的半径)，行星的体积

V=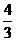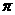R³，所以行星的平均密度==，

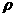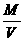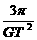即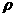T²=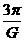，是一个常量，对任何行星都相同。

25、一均匀球体以角速度ω绕自己的对称轴自转，若维持球体不被瓦解的唯一作用力是万有引力，则此球的最小密度是多少？

分析与解：设球体质量为M，半径为R，设想有一质量为m的质点绕此球体表面附近做匀速圆周运动，则

G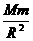=mω₀²R,　 所以，ω₀²=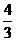πGρ。

由于ω≤ω₀得ω²≤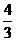πGρ，则ρ≥，即此球的最小密度为

24．侦察卫星在通过地球两极上空的圆轨道上运动，它的运动轨道距地面高度为h，要使卫星在一天的时间内将地面上赤道各处在日照条件下的情况全都拍摄下来，卫星在通过赤道上空时，卫星上的摄像机至少应拍摄地面上赤道圆周的弧长是多少?设地球的半径为R，地面处的重力加速度为g，地球自转的周期为

答案：侦察卫星绕地球做匀速圆周运动的周期设为T₁，则: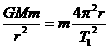　

地面处的重力加速度为g，则: 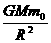=m₀g　 　　　　　　　　　　　　　

由上述两式得到卫星的周期T₁=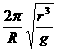　 其中r=h+R

地球自转的周期为T，在卫星绕行一周时，地球自转转过的角度为： θ=2π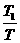

摄像机应拍摄赤道圆周的弧长为：s=Rθ　　　　

得：s=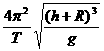

23．1990年3月，紫金山天文台将该台发现的2752号小行星命名为“吴健雄星”，将其看作为球形，直径约为32km，密度和地球接近，地球半径为6400km，若在该星球表面发射一颗卫星，则此速度为多大？答案．20m/s

22．假设地球自转速度达到使赤道上的物体“飘”起(完全失重)，估计一下地球上一天等于多少h？(地球赤道半径取6.4×10⁶m)。若要使地球的半面始终朝着太阳，另半面始终背着太阳，地球自转周期等于多少天。(g取10m/s²

答案：1.4h　 365

21、已知地球半径约为R=6.4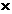10⁶m,又知月球绕地球的运动可近似看作匀速圆周运动，则可估算出月球到地球的距离约　 4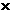10⁸m.　 m.(结果只保留一位有效数字)。

20、两颗人造卫星A、B绕地球做匀速圆周运动，周期之比为T_A:T_B=1:8，则轨道半径之比和运动速率之比分别为　　　　　 　　　　　　( 　　　　D 　　)

A．R_A:R_B = 4:1，υ_A: υ_B =1:2　　　　　　 B．R_A:R_B =4:1，υ_A: υ_B =2:1

C．R_A:R_B =1:4，υ_A: υ_B =1:2　　　　　 　D．R_A:R_B =1:4，υ_A: υ_B =2:1