
题目列表(包括答案和解析)
3、公式P=W/t求得的是功率的平均值。P=Fvcosα求得的是功率的瞬时值。当物体做匀速运动时,平均值与瞬时值相等。
2、应用公式W=Fscosα计算时,应明确是哪个力或哪些力做功、做什么功,同时还应注意:
(1)F必须是整个过程中大小、方向均不变的恒力,与物体运动轨迹和性质无关.当物体做曲线运动而力的方向总在物体速度的方向上,大小不变,式中α应为0,而s是物体通过的路程.
(2)公式中α是F、s之间夹角,在具体问题中可灵活应用矢量的分解;一般来说,物体作直线运动时,可将F沿s方向分解;物体作曲线运动时,应将s沿F方向分解,
(3)功是标量,但有正负,其正负特性由F与s的夹角α的取值范围反映出来.但必须注意,功的正负不表示方向,也不表示大小,其意义是表示物体与外界的能量转换.
(4)本公式只是计算功的一种方法,今后还会学到计算功的另外一些方法,尤其是变力做功问题,决不能用本公式计算,那时应灵活巧妙地应用不同方法,思维不能僵化.
1、做功的两个必备因素是力和在力方向上的位移.而往往某些力与物体的位移不在同一直线上,这时应注意这些力在位移方向上有无分力,确定这些力是否做功.
4、 探究隐含条件,构建物理模型。
例4.质量为m,电量为q的质点,在静电力作用下,以恒定速率v沿圆弧从A点运动到B点,其速度方向改变的角度为θ(弧度),AB弧长为s,则A、B两点间的电势差φA-φB=_________,AB弧中点场强大小E=___________。
点评:对此题,不少同学曾认为题目给出的条件模型不清,不能根据题目告诉的条件建立物理模型,因而后面的问题便无从下手,其实该题已给出了较隐蔽的条件。因为此质点只在静电力作用下以恒定速率v沿圆弧运动,故可以,此质点作匀速圆周运动,进而推断出此质点处,在点电荷形成的电场中,可以构建“电子绕核作圆周运动模型”,这样,隐含条件挖掘了出来,物理模型也就清晰了。
求解:
由点电荷形成的电场的特点可知,同一圆弧上各点电势相等,故φA-φB=0。
又由于质点的电场力提供了向心力,则质点在中点受到的电场力
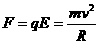 而R=s/θ
而R=s/θ
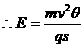
3、 探究问题的本质特征,构建物理模型。
例3.如图示,在竖直平面内,放置一个半径R很大的圆形光滑轨道,O为其最低点,在O点附近P处放一质量为m的滑块,求滑块由静止开始滑至O点时所需的时间。
 点评:滑块m向圆弧最低处滑动不同于沿斜面的滑动,这是一个很复杂的变速曲线运动,显然,牛顿定律不能求解,但滑块的运动轨迹是一段圆弧,其运动与受力单摆相同,则只要滑块满足从P点到O点的圆弧对应的圆心角很小,小于10°,则完全可以把滑块的运动等效为“单摆的运动模型”。
点评:滑块m向圆弧最低处滑动不同于沿斜面的滑动,这是一个很复杂的变速曲线运动,显然,牛顿定律不能求解,但滑块的运动轨迹是一段圆弧,其运动与受力单摆相同,则只要滑块满足从P点到O点的圆弧对应的圆心角很小,小于10°,则完全可以把滑块的运动等效为“单摆的运动模型”。
求解:
由单摆的周期公式有,滑块由P点滑到O点的时间为
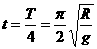
2、 紧扣关键词句,探究物理实质,构建物理模型。
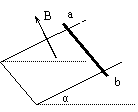
例2.如图示,一个U型导体框架,宽度为L=1m,其所在平面与水平面成α=30°角其电阻可忽略不计。设匀强磁场与U型框架的平面垂直,磁感应强度B=0.2T,今有一根导体棒ab,其质量m=0.2kg,有效电阻R=0.1Ω,跨放在U型框架上,并能无摩擦滑动,求导体ab下滑的最大速度vm。
点评:题中求“最大速度”几个字,是提示物理模型的关键性词句,最大,即不可增加,也就是导体ab将以此速度沿导轨斜向下作匀速直线运动。
据此,通过自己的抽象思维,大家可以在头脑中构建这样一幅物理图景:导体ab开始下滑时,速度v0=0,在斜轨上受下滑力(重力沿斜面分力),产生的加速度最大;随着下滑速度的增大→导体中感应电动势增加→感应电流增加→磁场对导体的安培力也增加,由于安培力与下滑力反向,故导体的加速度越来越小,而速度仍然越来越大,当下滑速度大到使安培力和下滑力平衡时,加速度为零,速度不再增加而以此最大速度作匀速直线运动。
求解:
 据上述模型分析,导体ab平衡的条件为:
据上述模型分析,导体ab平衡的条件为:
mgsinα=F安
而F安=BIL, I=ε/R, 又 ε=BLv
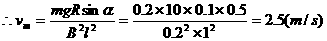
1、 探究物理过程,构建准确的物理模型。
例1.两块大小不同的圆形薄板(厚度不计),质量分别为M和m,(M=2m),半径分别为R和r,两板之间用一根长为L=0.4m的轻质绳相连结,开始时,两板水平叠放在支架C上方高h=0.2m处,如图示a示。以后,两板一起自由下落支架上有一个半径为R′(r<R′<R)的圆孔,两板中心与圆孔中心在同一直线上,大圆板碰到支架后跳起,机械能无损失。小圆板穿过圆孔,两板分离,试求当细绳绷紧的瞬间两板速度(如图示b)(取g=10m/s2)

点评:本题的整个过程可分为以下几个阶段:
⑴.两板自由下落。(此时两板作为一个整体可抽象为一个质点模型;其自由下落运动过程作为一个自由落体运动模型)
⑵.大圆板与支架相碰,且无能量损失,该瞬间的行为可作为一次“弹性碰撞”运动模型,而小圆板继续下落。
⑶.细绳绷紧瞬间,两板通过绳的相互作用获得共同速度,可作为一个“完全非弹性碰撞运动模型。
求解:
两板落至支架C时的速度: 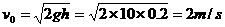
大圆板与支架C碰后以速度为初速度竖直跳起,设至细绳绷紧前历时t1,绷紧前的速度为v1,上跳高度为(离支架的C的高度)为h1,则:
v1= v0-g t1 ……………………………………………………………………①
v12=v02-2gh1 ……………………………………………………………………②
小圆板穿过圆孔时的速度为v0,设落至细绳绷紧前历时t2,速度为v2,下落高度(离支架C的高度)为h2,则:
v2= v0+g t2 ……………………………………………………………………③
v22=v02-2gh2 ……………………………………………………………………④
据题意有:t1=t2,h1+h2=L=0.4m,故
由①③两式有: v1+v2=2v0=4m/s ……………………………………⑤
由②④两式有: v22-v12=2gL=2×10×0.4=8(m/s)2 ………………⑥
由⑤⑥两式可得绳绷紧前两板速度大小分别为:
v1=1m/s v2=3m/s
方向:v1 向上 v2向下
由于细绳绷紧时间极短,重力的冲量可忽略,故绷紧过程中系统动量守恒。设两板共同速度为u,取竖直方向为正,由动量守恒定律有:
mv2-Mv1=(m+M)v 得
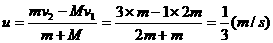
即该瞬间两板获得向下的共同速度为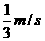 。
。
16.(15分)将氢原子中的电子的运动看作是绕氢核做匀速圆周运动,这时在研究电子运动的磁效应时,可将电子的运动等效为一环形电流,环的半径等于电子的轨道半径r。现对一氢原子加上一磁场,磁场的磁感应强度大小为B,方向垂直电子的轨道平面,这时电子运动的等效电流用I1来表示,现将外磁场反向,但磁场的磁感应强度大小不变,仍为B,这时电子运动的等效电流用I2来表示,假设在加上外磁场以及外磁场反向时,氢核的位置、电子运动的轨道平面以及轨道半径都不变,求外磁场反向后电子运动的等效电流的差,即│I1一I2│等于多少?用m和e表示电子的质量和电量。
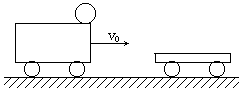
15.(15分)平直的轨道上有一节车厢,车厢以12m/s的速度做匀速直线运动,某时刻与一质量为其一半的静止的平板车挂接时,车厢顶边缘上一个小钢球向前滚出,如图所示,平板车与车厢顶高度差为1.8m,设平板车足够长,求钢球落在平板车上何处?(g取10m/s2)
14.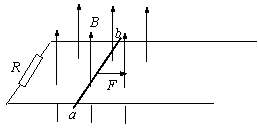 (10分)如图所示,导体棒ab在磁感应强度为B、方向竖直向上的匀强磁场中受水平恒力F作用,以速度v沿光滑导轨匀速向右运动。导轨左端所接电阻为R,导轨自身电阻不计,导体棒电阻为r,导轨间距为L。请你从力F做功与电路中消耗能量的关系证明:导体棒ab中的感应电动势为
(10分)如图所示,导体棒ab在磁感应强度为B、方向竖直向上的匀强磁场中受水平恒力F作用,以速度v沿光滑导轨匀速向右运动。导轨左端所接电阻为R,导轨自身电阻不计,导体棒电阻为r,导轨间距为L。请你从力F做功与电路中消耗能量的关系证明:导体棒ab中的感应电动势为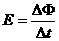 ,并说明其物理意义。
,并说明其物理意义。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com