
题目列表(包括答案和解析)
4、动能定理与牛顿运动定律的比较
用牛顿运动定律解题涉及到的有关物理量比较多,如F、a、m、v、s、t等.对运动过程的细节变化也要掌握得比较充分,才可列式求解。而运用动能定理解题涉及到的物理量只有F、s、m、v.它对运动过程的细节及其变化也不要求了解,只需考虑始末两状态的动能和外力做的功,它还可把不同运动过程合并成一个全过程来处理,使解题过程简便.当然,如果题目中要求了解加速度a、运动时间t等细节,那就需要从动力学、运动学的角度去分析,不能直接求解了。
 例
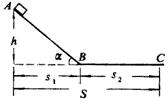
如图所示,小滑块从斜面顶点4由静止滑至水平部分C点而停止.已知斜面高为h,滑块运动的整个水平距离为s.求小滑块与接触面间的动摩擦因数(设滑块与各部分的动摩擦因数相同).
例
如图所示,小滑块从斜面顶点4由静止滑至水平部分C点而停止.已知斜面高为h,滑块运动的整个水平距离为s.求小滑块与接触面间的动摩擦因数(设滑块与各部分的动摩擦因数相同).
解 滑块从A点滑到C点,只有重力和摩擦力做功,设滑块质量为m,动摩擦因数为μ,斜面倾角为α,斜面底边长s1,水平部分长s2,由动能定理得:
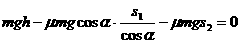
得μ=h/s
由此题可见,用动能定理求解,回避了加速度a,不必考虑细节,解题过程简单很多.
3、结合运动分解,运用动能定理
例 如图所示,某人通过过一根跨过定滑轮的轻绳提升一个质量为m的重物,开始时人在滑轮的正下方,绳下端A点离滑轮的距离为H。人由静止拉着绳向右移动,当绳下端到B点位置时,人的速度为v,绳与水平面夹角为θ。问在这个过程中,人对重物做了多少功?
解 人移动时对绳的拉力不是恒力,重物不是做匀速运动也不是作匀变速运动,故无法用W=Fscosθ求对重物作的功,需从动能定理的角度来分析求解.
当绳下端由A点移到B点时,重物上升的高度为:
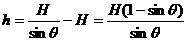
重力做功的数值为: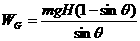
当绳在B点实际水平速度为v时,v可以分解为沿绳斜向下的分速度v1和绕定滑轮逆时针转动的分速度v2,其中沿绳斜向下的分速度v1和5重物上升速度的大小是一致的,从图中可看出:v1=vcosθ
以重物为研究对象,根据动能定理得: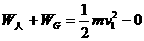
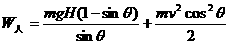
2、结合隔离法,运用动能定理
 例
质量为M的列车,沿平直轨道匀速前进,质量为m的末节车厢中途脱钩,当司机发觉时,机车已行驶L距离,于是他立即关闭油门,撤去牵引力。设车运动的阻力与重力成正比,机车的牵引力为定值,当列车的两部分都停止运动时,它们的距离是多少?
例
质量为M的列车,沿平直轨道匀速前进,质量为m的末节车厢中途脱钩,当司机发觉时,机车已行驶L距离,于是他立即关闭油门,撤去牵引力。设车运动的阻力与重力成正比,机车的牵引力为定值,当列车的两部分都停止运动时,它们的距离是多少?
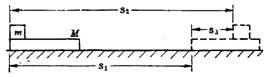
解 此题牵涉机车和车厢这两个研究对象,它们又分别经历着不同的变速运动过程.如果从动力学、运动学角度去分析求解将非常麻烦.我们运用隔离法针对每一个研究对象运动的全过程分析其受力,画出其运动的示意图如图所示,并分别列出它们动能定理的表达式:
未脱钩时,整列车匀速前进,有:F=KMg (1)
脱钩后,两车分别作加速、减速运动
对机车:FL-K(M-m)gs1=0-(M-m)v02/2 (2)
对车厢:-Kmgs2=0-mv02/2 (3)
将(1)代入(2)后再将等式两边分别与(3)相除,化简,得:
 Δs=s1-s2=ML/(M-m)
Δs=s1-s2=ML/(M-m)
1、灵活选取适当过程,运用动能定理
例 量过为4kg的铅球,从离沙坑1.8m的高处自由落下.铅球落进沙坑后陷入0.2m深而停止运动,求沙坑对铅球的平均阻力(g取10m/2).
解 铅球在前一段作自由落体运动,后一段作匀减速运动.对前一段可用机械能守恒求解,后一段可用动能定理求解.但如果我们把开始下落到最终停止看成一个过程,运用动能定理列式,将很快得到结果:
由W=ΔEk 可得:mg(h+s)-fs=0-0=0
f=(h+s)mg/s=(1.8+0.2)×4×10/0.2=400N
此题我们用动能定理列式时,把两段过程处理成一个过程,求解就便捷得多了.
2、交通工具起动时的牵引力及功率
汽车等交通工具的起动方式有两种:一是以恒定功率起动,二是汽车以恒定的牵引力起动,具体分析如下:
(1)输出功率不变时的运动
 由于牵引力F=P/v,随着速度v的增大,牵引力F减小,则加速度a=(F-f)/m减小,但因a与v同向,汽车的速度v不断增大,F减小,a减小,直至a=0时,汽车作匀速运动,此时速度为最大值vm=P/F=P/f,在此之前,由牛顿第二定律得:(P/v)-f=ma,可知任一速度值均有与之相对应的一个确定的加速度值.由于汽车做变加速运动,所以不能用匀变速直线运动的公式求解,也不能对全过程应用牛顿第二定律,但动能定理是适用的,力和加速度瞬时对应关系也成立,因此解题时通常是对某一过程列动能定理方程,对某一瞬时列牛顿第二定律方程.
由于牵引力F=P/v,随着速度v的增大,牵引力F减小,则加速度a=(F-f)/m减小,但因a与v同向,汽车的速度v不断增大,F减小,a减小,直至a=0时,汽车作匀速运动,此时速度为最大值vm=P/F=P/f,在此之前,由牛顿第二定律得:(P/v)-f=ma,可知任一速度值均有与之相对应的一个确定的加速度值.由于汽车做变加速运动,所以不能用匀变速直线运动的公式求解,也不能对全过程应用牛顿第二定律,但动能定理是适用的,力和加速度瞬时对应关系也成立,因此解题时通常是对某一过程列动能定理方程,对某一瞬时列牛顿第二定律方程.
例 辆机车的质量为750T,沿平直轨道由静止开始运动.它以额定功率在5分钟内驶过2.5km,并达到10m/s的最大速度.求:(1)机车发动机的额定功率P和机车与轨道间的摩擦因数μ分别是多少?(2)当机车速度为5m/s时的加速度多大(g取10m/s2)
解 图所示,设机车在A处起动,因功率不变,故随着速度的增大,牵引力减小,加速度减小,机车做变加速运动.当牵引力减小到F=f的B处时,速度达到最大值vm,以后机车做匀速运动.
(1)由动能定理得:Pt-μmgs=mvm2/2 ①
在B处:F=f=μmg,故有P=Fv=μmgvm ②
将②式代人①式、并代入数据可得:
μ=0.01
再将μ值代入②式得:
P=7.5×105J
(2)设此时牵引力为F’,则
F’=P/v’=7.5×105/5=1.5×105N
再由F’-f=ma得
a=(F’-f)/m=0.1m/s2
例 出功率保持10kw的起重机起吊500kg的重物,当货物升高到2m时速度达到最大值,此最大速度是多少?此过程用了多长时间?(g取10m/s2)
解 重机以恒定的功率吊起重物的过程是加速度不断减小、速度不断增大的过程.当货物的速度达到最大时,起重机的牵引力与货物的重力相平衡,即:
F=mg=5×103N,vm=P/F=2m/s.
求解这一段运动时间不能用匀变速运动的公式,我们可以货物为研究对象运用动能定理求解:
Pt-WG=mv2/2, t=(mv2/2+mgh)/P=1.1s
(2)牵引力不变时的运动
汽车以恒定的牵引力起动,则汽车开始一段时间作匀加速运动,由v=at及P=Fv=Fat可知,随时间的延长汽车的功率越来越大,直到达到其最大功率时,输出功率不能再增大,但此时由于牵引力仍大于阻力,汽车仍加速,则因受最大功率的制约,牵引力必须减小,汽车做加速度越来越小的匀加速运动,直至a=0时做匀速运动,故此种情形下,汽车前一阶段做匀加速运动,后一阶段做变加速运动。在汽车做匀加速运动阶段中, 我们既可以运用功的公式、动能定理来求解,也可以运用牛顿运动定律来求解.对变加速运动阶段,则必须用第(1)点的方法求解.
例 车的质量为m,它在运动中受到的阻力f恒定不变。汽车发动机的额定功率为P,求:(1)汽车在作匀加速运动时的长大速度是多少?(2)汽车从静止出发作加速度为a的匀加速运动的时间不应超过多少?
解 车受到的阻力一定,且又做的是匀加速运动,所以它受到的牵引力也是一定的.
F-f=ma
随着速度的增加,汽车的输出功率也在不断增大.当输出功率达到额定功率时,这时汽车行驶的速度不允许再增加了.此时有:
vm=P/F=P/(ma+f)
再根据运动学公式,可求出这段过程所需时间:
t=vm/a=P/[(ma+f)a]
1、重力的功率
(1)自由落体过程中重力的功率
(2)平抛运动中重力的功率
(3)沿斜面滑行的物体的重力的功率
例 质量为m的物体,由静止开始沿倾角为θ的光滑斜面下滑,求前3s内、第3s内、第3s末重力做功的功率。
解 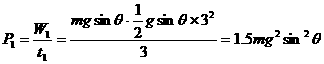

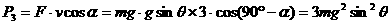
3、变力做功
大小或方向变化的力所做的功,一般不能用功的公式W=Fscosα去求解.需变换思维方式,独辟蹊径求解。
(1)用功率定义式求解
将功率的定义式P=W/t变形,得W=Pt。在求解交通工具牵引力做功问题时经常用到此公式。
例 质量为m的汽车在平直公路上以初速度v0开始匀加速行驶,经时间t前进距离s后,速度达最大值vm,设在这段过程中发动机的功率恒为P,汽车所受阻力恒为f,则在这段时间内发动机所做的功为:
A、Pt B、fvMt
C、fs+mvm2/2 D、mvm2/2-mv02/2+fs
(答案:ABD)
(2)用动能定理求解变力做功
 求解某个变力所做的功,可以利用动能定理,通过动能改变量和其余力做功情况来确定。
求解某个变力所做的功,可以利用动能定理,通过动能改变量和其余力做功情况来确定。
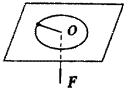
例 如图所示,把一小球系在轻绳的一端,轻绳的另一端穿过光滑木板的小孔,且受到竖直向下的拉力作用.当拉力为F时,小球做匀速圆周运动的轨道半径为R.当拉力逐渐增至4F时,小球匀速圆周运动的轨道半径为R/2.在此过程中,拉力对小球做了多少功?
解 此题中的F是一个大小变化的力,故我们不能直接用功的公式求解拉力的功.
根据F=mv2/R,我们可分别求得前、后两个状态小球的动能,这两状态动能之差就是拉力所做的功.
由F=mv12/R 4F=mv22/0.5R
得WF=mv22/2-mv12/2=FR/2
 例
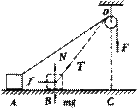
如图,用F=20N的恒力拉跨过定滑轮的细绳的一端,使质量为10kg的物体从A点由静止沿水平面运动.当它运动到B点时,速度为3m/s.设OC=4m,BC=3m,AC=9.6m,求物体克服摩擦力做的功.
例
如图,用F=20N的恒力拉跨过定滑轮的细绳的一端,使质量为10kg的物体从A点由静止沿水平面运动.当它运动到B点时,速度为3m/s.设OC=4m,BC=3m,AC=9.6m,求物体克服摩擦力做的功.
解 作出物体在运动过程中的受力图。其中绳的拉力T大小不变,但方向时刻改变.N随T方向的变化而变化(此力不做功).f随正压力N的变化而变化.因此对物体来说,存在着两个变力做功的问题.但绳拉力T做的功,在数值上应等于向下恒力F做的功.F的大小已知,F移动的距离应为OA、OB两段绳长之差.
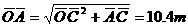
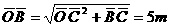
由动能定理 WF+Wf=ΔEk 得:
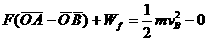
Wf=-63(J)
即物体克服摩擦力做了63J耳的功.
(3)用图象法求解变力做功
如果能知道变力F随位移s变化的关系,我们可以先作出F-s关系图象,并利用这个图象求变力所做的功.
 [例]如图,密度为ρ,边长为a的正立方体木块漂浮在水面上(水的密度为ρ0).现用力将木块按入水中,直到木块上表面刚浸没,此过程浮力做了多少功?
[例]如图,密度为ρ,边长为a的正立方体木块漂浮在水面上(水的密度为ρ0).现用力将木块按入水中,直到木块上表面刚浸没,此过程浮力做了多少功?
解 未用力按木块时,木块处于二力平衡状态
F浮=mg 即ρ0ga2(a-h)=ρga3
并可求得:h=a(ρ0-ρ)/ρ0(h为木块在水面上的高度)
在用力按木块到木块上表面刚浸没,木块受的浮力逐渐增大,上表面刚浸没时,浮力达到最大值:F’浮=ρ0ga3
以开始位量为向下位移x的起点,浮力可表示为:
F浮=ρga3+ρ0ga2x
根据这一关系式,我们可作出F浮-x图象(如图右所示).在此图象中,梯形OhBA所包围的“面积”即为浮力在此过程所做的功。
W=(ρ0ga3+ρga3)h/2=ga3h(ρ0+ρ)/2
这里的“面积”为什么就是变力所做的功?大家可结合匀变速运动的速度图象中的“面积”表示位移来加以理解.即使F-x关系是二次函数的关系,它的图象是一条曲线,这个“面积”仍是变力在相应过程中所做的功.
2、判断做功正负的方法
(1)从力与位移或速度方向的关系进行判断。
如:“子弹打木块”问题,摩擦力对子弹做负功,对木块做正功。
例 如图所示,质量为M的木块静止在光滑水平面上,质量为m的子弹以水平速度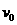 射
射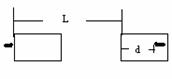 中与木块一起以速度v运动,已知当子弹相对木块静止时,木块前进距离为L,子弹进入木块的深度为d,若木块对子弹的阻力F恒定,那么下列关系式中正确的是( )、、
中与木块一起以速度v运动,已知当子弹相对木块静止时,木块前进距离为L,子弹进入木块的深度为d,若木块对子弹的阻力F恒定,那么下列关系式中正确的是( )、、
A、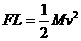 B、
B、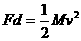
C、 D、
D、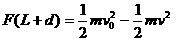
(2)从能量的增减进行判断
例 如图示,在质量不计、长度为L的直杆一端和中点分别固定一个质量都是m的小球A和B,试判断当杆从水平位置无摩擦地转到竖直位置的过程中,杆对A、B球做功的正负。
 解 A、B两球组成的系统的机械能守恒,由机械能守恒定律:
解 A、B两球组成的系统的机械能守恒,由机械能守恒定律:
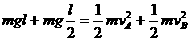
由于两球在同一杆上,角速度相等,故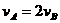
解之得: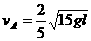 ,
,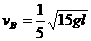
与A、B球自由下落时的速度比较,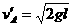 ,
,

可见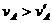 ,
,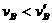 ,故杆对A球做正功,对B球做负功。
,故杆对A球做正功,对B球做负功。
1、恒力做功
求解恒力功的方法一般是用功的定义式W=Fscosα,需要特别注意:
(1)位移s的含义:是力直接作用的物体对地的位移。当力在物体上的作用位置不变时,s就是力作用的那个质点的位移;当力在物体上的作用位置不断改变时,s应是物体的位移。如:一个不能视为质点的物体受到滑动摩擦力作用时,摩擦力的作用点时时变化,此时s就不是摩擦力作用点的位移,而是物体的位移。
 例
如图示,质量为m、初速为v0的小木块,在桌面上滑动。动摩擦因数为μ,求木块停止滑动前摩擦力对木块和桌面所做的功。
例
如图示,质量为m、初速为v0的小木块,在桌面上滑动。动摩擦因数为μ,求木块停止滑动前摩擦力对木块和桌面所做的功。
解 对木块:W1=-fs=-μmg·v02/(2gμ)=-mv02/2
 对桌面:W2=0
对桌面:W2=0
例 如图示,质量为m、初速为v0的小木块,在一块质量为M的木板上滑动,板放在光滑水平桌面上,求木块和板相对静止前,摩擦力对木块和木板所做的功。
解 据动量守恒mv0=(m+M)v得
W1=-fs2=-μmg·M(M+2m)v02/(M+m)22gμ=-Mm(M+2m)v02/2(M+m)2
W2=fs1=Mm2v02/2(M+m)2gμ
(2)一对相互作用力所做功之和不一定为零
如:人竖直向上跳起,地面对人的作用力对人做正功,人对地而不做功(地球位移视为零),总功为正;
一对静摩擦力,位移值一定相同,总功必为零;
一对滑动摩擦力,做功时必然发热,系统内能增加,总功必为负。转化为内能值为 
14、应用机械能守恒定律解题的一般步骤:
(1)认真审题,确定研究对象;
(2)对研究对象进行受力分析和运动过程、状态的分析,弄清整个过程中各力做功的情况,确认是否符合机械能守恒的条件;
(3)确定一个过程、两个状态(始末),选取零势能参考平面,确定始末状态的动能、势能值或这个过程中ΔEp和ΔEk的值;
(4)利用机械能守恒定律列方程,必要时还要根据其它力学知识列出联立方程;
(5)统一单位求解.
解题的关键是准确找出始、末状态的动能和势能的值,尤其是势能值的确定.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com