
题目列表(包括答案和解析)
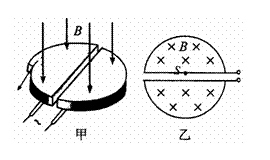
14.(2006年4月西城二模)(20分)在高能物理研究中,粒子回旋加速器起着重要作用,如图甲为它的示意图。它由两个铝制D型金属扁盒组成,两个D形盒正中间开有一条窄缝。两个D型盒处在匀强磁场中并接有高频交变电压。图乙为俯视图,在D型盒上半面中心S处有一正离子源,它发出的正离子,经狭缝电压加速后,进入D型盒中。在磁场力的作用下运动半周,再经狭缝电压加速。如此周而复始,最后到达D型盒的边缘,获得最大速度,由导出装置导出。已知正离子的电荷量为q,质量为m,加速时电极间电压大小为U,磁场的磁感应强度为B,D型盒的半径为R。每次加速的时间很短,可以忽略不计。正离子从离子源出发时的初速度为零。
(1)为了使正离子每经过窄缝都被加速,求交变电压的频率;
(2)求离子能获得的最大动能;
(3)求离子第1次与第n次在下半盒中运动的轨道半径之比。
13.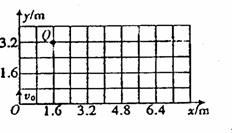 (2006年湖北十六校联考)(19分)如图所示,在竖直平面内建立xOy直角坐标系,Oy表示竖直向上的方向,已知该平面内存在沿x轴负方向的区域足够大的匀强电场,现有一个带电量为2.5×10-4C的小球从坐标原点O沿y轴正方向以0.4kg·m/s的初动量竖直向上抛出,它到达的最高点位置为图中的Q点,不计空气阻力,g取10m/s2。
(2006年湖北十六校联考)(19分)如图所示,在竖直平面内建立xOy直角坐标系,Oy表示竖直向上的方向,已知该平面内存在沿x轴负方向的区域足够大的匀强电场,现有一个带电量为2.5×10-4C的小球从坐标原点O沿y轴正方向以0.4kg·m/s的初动量竖直向上抛出,它到达的最高点位置为图中的Q点,不计空气阻力,g取10m/s2。
⑴指出小球带何种电荷。
⑵求匀强电场的电场强度的大小。
⑶求小球从O点抛出到落回x轴的过程中,电势能的改变量。
12.
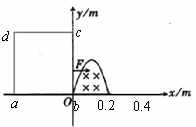 (福州市2006)(20分) 如图所示,在一个被x轴与曲线为边界包围的空间中存在匀强磁场,曲线方程
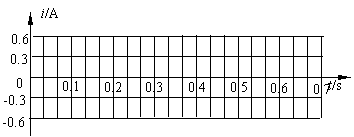
(福州市2006)(20分) 如图所示,在一个被x轴与曲线为边界包围的空间中存在匀强磁场,曲线方程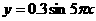 (单位:m)(0≤x≤0.2m).磁场方向垂直纸面向里,磁感应强度B = 0.2T.有一正方形金属线框边长是0.4 m,线框总电阻是0.1Ω, 它的ab边与x轴重合.在拉力F的作用下,线框以1.0 m/s的速度水平向右匀速运动.试求:(1)在线框通过该磁场区域的过程中,拉力F的最大瞬时功率是多少?
(单位:m)(0≤x≤0.2m).磁场方向垂直纸面向里,磁感应强度B = 0.2T.有一正方形金属线框边长是0.4 m,线框总电阻是0.1Ω, 它的ab边与x轴重合.在拉力F的作用下,线框以1.0 m/s的速度水平向右匀速运动.试求:(1)在线框通过该磁场区域的过程中,拉力F的最大瞬时功率是多少?
(2)在下面坐标中画出线框产生的电流随时间的变化图象(取a→b→c→d→a方向为电流正方向)。 (3)线框拉过磁场区拉力F做多少功?
计算论述题专项训练(五)
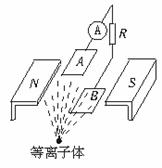
11.(2006年3月温州).目前,世界上正在研究一种新型发电机叫磁流体发电机。如图所示表示了它的发电原理:将一束等离子体垂直于磁场方向喷入磁场,在磁场中有两块金属板A、B,这时金属板上就会聚集电荷,产生电压。如果射入的等离子体速度均为v,两金属板的板长为L,板间距离为d,板平面的面积为S,匀强磁场的磁感应强度为B,方向垂直于速度方向,负载电阻为R,等离子体充满两板间的空间。当发电机稳定发电时,电流表示数为I,那么板间等离子体的电阻率为多少?
10.(湖北八市2006年3月)1997年8月26日在日本举行的国际天文学大会上,德国Max Planck学会的一个研究组宣布了他们的研究成果:银河系的中心可能存在一个大“黑洞”,它的质量十分巨大,以致于其速度有可能超过真空中的光速,因此任何物体都不能脱离它的束缚,甚至连光也不能射出,我们无法看到它,所以叫“黑洞”。
(1)根据长期观察发现,该“黑洞”能使距其60亿千米的某个星体以2000km/s的速度绕其旋转,若视星体做匀速圆周运动,试求该“黑洞”的质量。
(2)根据天体物体学知识,物体从地球上脱离的速度(第二宇宙速度)是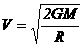 ,M、R分别表示地球的质量和半径,根据(1)的条件,试求该“黑洞”的可能最大半径。(万有引力常量
,M、R分别表示地球的质量和半径,根据(1)的条件,试求该“黑洞”的可能最大半径。(万有引力常量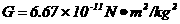 )
)
9. (2006年4月西城二模)(18分)如图所示,两根足够长的直金属导轨MN、PQ平行放置在倾角为θ的绝缘斜面上,两导轨间距为L。M、P两点间接有阻值为R的电阻。一根质量为m的均匀直金属杆ab放在两导轨上,并与导轨垂直。整套装置处于匀强磁场中,磁场方向垂直于斜面向上。导轨和金属杆的电阻可忽略。让金属杆ab沿导轨由静止开始下滑,经过足够长的时间后,金属杆达到最大速度vm,在这个过程中,电阻R上产生的热为Q。导轨和金属杆接触良好,它们之间的动摩擦因数为μ,且μ<tanθ。已知重力加速度为g。
(2006年4月西城二模)(18分)如图所示,两根足够长的直金属导轨MN、PQ平行放置在倾角为θ的绝缘斜面上,两导轨间距为L。M、P两点间接有阻值为R的电阻。一根质量为m的均匀直金属杆ab放在两导轨上,并与导轨垂直。整套装置处于匀强磁场中,磁场方向垂直于斜面向上。导轨和金属杆的电阻可忽略。让金属杆ab沿导轨由静止开始下滑,经过足够长的时间后,金属杆达到最大速度vm,在这个过程中,电阻R上产生的热为Q。导轨和金属杆接触良好,它们之间的动摩擦因数为μ,且μ<tanθ。已知重力加速度为g。
(1)求磁感应强度的大小;
(2)金属杆在加速下滑过程中,当速度达到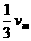 时,求此时杆的加速度大小;
时,求此时杆的加速度大小;
(3)求金属杆从静止开始至达到最大速度的过程中下降的高度。
计算论述题专项训练(四)
8.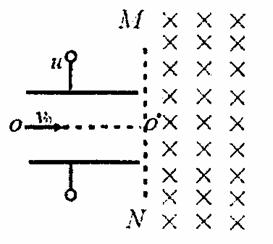 (2006年合肥)如图所示,两平行金属板的板长l=0.2m,两板间距离为d=0.2m,板间的电压u随时间t变化的关系为u=141sin100
(2006年合肥)如图所示,两平行金属板的板长l=0.2m,两板间距离为d=0.2m,板间的电压u随时间t变化的关系为u=141sin100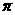 t(V),紧靠金属右侧的虚线MN的右边是较大的匀强磁场区域,磁感应强度为B,方向垂直纸面向里。现有带正电的粒子连续不断地以速度V0=105m/s,沿中线OO‘射入两板间。已知带电粒子的比荷
t(V),紧靠金属右侧的虚线MN的右边是较大的匀强磁场区域,磁感应强度为B,方向垂直纸面向里。现有带正电的粒子连续不断地以速度V0=105m/s,沿中线OO‘射入两板间。已知带电粒子的比荷 ,粒子的重力和粒子间相互作用力均忽略不计。t=0时刻射入电场的带电粒子穿越电场进入磁场后,离开磁场时到O’点的距离为S0=0.2m。
,粒子的重力和粒子间相互作用力均忽略不计。t=0时刻射入电场的带电粒子穿越电场进入磁场后,离开磁场时到O’点的距离为S0=0.2m。
(1) 证明:能从两板间穿出的所有粒子,经边界线MN进入磁场和离开磁场时两位置间的距离为S0
(2) 求经过电场进入磁场的带电粒子在离开磁场时到O‘点的最大距离。
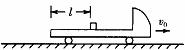
7.(武汉2006年3月)如图所示,一面板车以某一速度v0匀速行驶,某时刻一货箱(或视为质点)无初速度地放置于平板车上,货箱离车后端的距离为l=3m,货箱放入车上的同时,平板车开始刹车,刹车过程可视为做a=4m/s2的匀减速直线运动。已知货箱与平板车之间的动摩擦因数为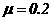 ,g=10m/s2,为使货箱不从平板车上掉下来,平板车匀速行驶的速度v0应满足什么条件?
,g=10m/s2,为使货箱不从平板车上掉下来,平板车匀速行驶的速度v0应满足什么条件?
6.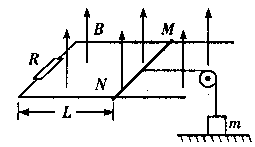 (2005北京西城区)如图。不计电阻的U形导轨水平放置,导轨宽
(2005北京西城区)如图。不计电阻的U形导轨水平放置,导轨宽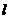 =0.5m,左端连接阻值为0.4
=0.5m,左端连接阻值为0.4 的电阻R。在导轨上垂直于导轨放一电阻为0.1
的电阻R。在导轨上垂直于导轨放一电阻为0.1 的导体棒MN,并用水平轻绳通过定滑轮吊着质量为m=2.4g的重物,图中L=0.8m。开始重物与水平地面接触并处于静止。整个装置处于竖直向上的匀强磁场中,磁感应强度B0=0.5T,并且以
的导体棒MN,并用水平轻绳通过定滑轮吊着质量为m=2.4g的重物,图中L=0.8m。开始重物与水平地面接触并处于静止。整个装置处于竖直向上的匀强磁场中,磁感应强度B0=0.5T,并且以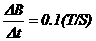 的规律在增大。不计摩擦阻力。求至少经过多长时间才能将重物吊起?(g=10m/s2)
的规律在增大。不计摩擦阻力。求至少经过多长时间才能将重物吊起?(g=10m/s2)
2-1.(1)上升时间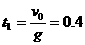 s 上升高度h=
s 上升高度h=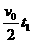 =0.8m
=0.8m
下落时间H+h=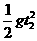 ,解得
,解得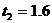 s A物体运动的总时间为:t=t1+t2=2s
s A物体运动的总时间为:t=t1+t2=2s
(2)AB一起匀速上升时,绳子的拉力为F=(mA+mB)g=2mg(2分)
B加速上升时,由F-mg=ma可得a=10m/s2 (2分)
重物A落地时,重物B的速度由vt=v0+at(2分) 解得vt=24m/s (2分)
2-2.⑴ 滑块A从光滑曲面上h高处由静止开始滑下的过程,机械能守恒,设其滑到底面的速度为v1 ,由机械能守恒有: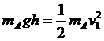 ① 解之得
① 解之得 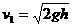 ②
②
滑块A与B碰撞的过程,A、B系统的动量守恒,碰撞结束瞬间具有共同速度设为v2 ,由动量守恒定律有: 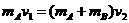 ③ 解之得:
③ 解之得: 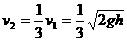 ④
④
(2)滑块A、B发生碰撞后与滑块C一起压缩弹簧,压缩的过程机械能守恒,被压缩弹簧的弹性势能最大时,滑块A、B、C速度相等,设为速度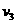 ,
,
由动量守恒: 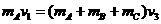 ⑤
⑤
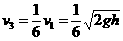 ⑥
⑥
由机械能守恒定律有:
EPmax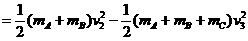 ⑦ EPmax
⑦ EPmax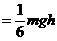 ⑧
⑧
(3)被压缩弹簧再次恢复自然长度时,滑块C脱离弹簧,设滑块A、B的速度为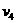 ,滑块C的速度为
,滑块C的速度为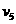 ,分别由动量守恒定律和机械能守恒定律有:
,分别由动量守恒定律和机械能守恒定律有:
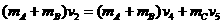 ⑨
⑨
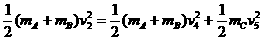 ⑩
⑩
解之得: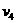 = 0,
= 0, 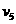 =
=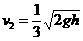 ⑾
⑾
C从桌面边缘飞出做平抛运动:S = 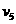 t ⑿ H=
t ⑿ H=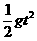 ⒀ 解得:S =
⒀ 解得:S = 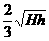 ⒁
⒁
2-3.当重物被吊起时:BIL=mg, 而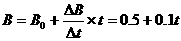
感应电动势: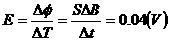 感应电流:
感应电流: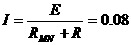 (A)由以上可知:t=1s。
(A)由以上可知:t=1s。
计算论述题专项训练(三)
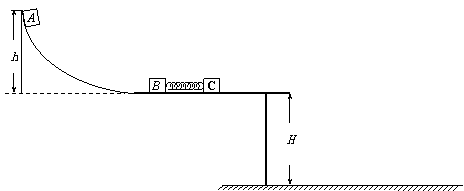
5.(2006年昆明市一模) (20分)如图所示,一轻质弹簧的一端固定在滑块B上,另一端与滑块C接触但未连接,该整体静止放在离地面高为H的光滑水平桌面上.现有一滑块A从光滑曲面上离桌面h高处由静止开始滑下,与滑块B发生碰撞并粘在一起压缩弹簧推动滑块C向前运动,经一段时间,滑块C脱离弹簧,继续在水平桌面上匀速运动一段后从桌面边缘飞出.已知mA=m,mB=2m,mC=3m,求:(1)滑块A与滑块B碰撞结束瞬间的速度;(2)被压缩弹簧的最大弹性势能; (3) 滑块C落地点与桌面边缘的水平距离.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com