
题目列表(包括答案和解析)
4.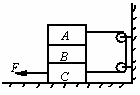 如图所示,轻绳两端分别与A、C两物体相连接,mA=1kg,mB=2kg,mC=3kg,物体A、B、C及C与地面间的动摩擦因数均为μ=0.1,轻绳与滑轮间的摩擦可忽略不计.若要用力将C物拉动,则作用在C物上水平向左的拉力最小为(取g=10m/s2)
如图所示,轻绳两端分别与A、C两物体相连接,mA=1kg,mB=2kg,mC=3kg,物体A、B、C及C与地面间的动摩擦因数均为μ=0.1,轻绳与滑轮间的摩擦可忽略不计.若要用力将C物拉动,则作用在C物上水平向左的拉力最小为(取g=10m/s2)
A.6N B.8N C.10N D.12N
3.某同学把一体重秤放在电梯的地板上,他站在体重秤上随电梯运动并观察体重秤示数的变化情况.下表记录了几个特定时刻体重秤的示数.(表内时间不表示先后顺序)
|
时 间 |
t0 |
t1 |
t2 |
t3 |
|
体重秤示数/kg |
45.0 |
50.0 |
40.0 |
45.0 |
若已知t0时刻电梯静止,则下列说法错误的是
A.t1和t2时刻该同学的质量并没有变化,但所受重力发生变化;
B.t1和t2时刻电梯的加速度方向一定相反;
C.t1和t2时刻电梯的加速度大小相等,运动方向不一定相反;
D.t3时刻电梯可能向上运动
2.在平坦的垒球运动场上,击球手挥动球棒将垒球水平击出,垒球飞行一段时间后落地.若不计空气阻力,则
A.垒球落地时的动能等于飞行过程中重力对球做的功
B.垒球落地时的速度方向与水平地面垂直
C.垒球在空中运动的时间仅由击球点离地面的高度决定
D.垒球在空中运动的水平位移仅由初速度决定
1.某车队从同一地点先后从静止开出n辆汽车,在平直的公路上沿一直线行驶,各车均先做加速度为a的匀加速直线运动,达到速度v后做匀速直线运动,汽车都匀速行驶后,相邻两车距离均为s,则相邻两车启动的时间间隔为
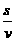
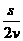
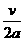

A. B. C. D.
13.(17分)①将F沿水平方向、竖直方向分解,冰块受的支持力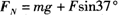 (3分)
(3分)
摩擦力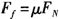 (1分)在前一阶段,对冰块由动能定理:
(1分)在前一阶段,对冰块由动能定理:
 (4分)
(4分)
联立以上各式,并将x1=4.00m等代入,解出υ1=1.00m/s. (2分)
②冰块做类平抛运动,沿x轴方向 . 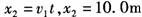 (2分)
(2分)
沿Y轴方向,由牛顿第二定律: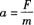 (2分)
(2分)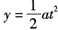 。 (2分)
。 (2分)
联立解出y=52.0m>5m,故冰块碰不到仪器室. (1分)
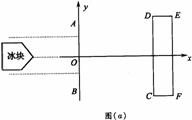
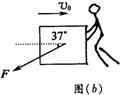
18.(20分)某边防哨所附近的冰山上,突然发生了一次“滑坡”事件,一块质量m=840kg的冰块滑下山坡后,又在水平地面上向着正前方的精密仪器室[见图(a)中的CDEF]冲去.值勤的战士目测了一下现场情况,冰块要经过的路线分前、后两段,分界线为AB,已知前段路面与冰块的动摩擦因数μ=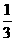 ,后段路面与冰块的动摩擦因数很小可忽略不计.为防止仪器室受损,又由于场地限制他只能在前一段中,逆着冰块滑来的方向与水平成370角斜向下用F=875N的力推挡冰块,如图(b)所示,此时冰块的速度为υ0=6.00m/s,在第一路段沿直线滑过4.00m后,到达两段的分界线.以分界线为y轴,冰块的运动方向为x轴建立平面直角坐标系.冰块进入光滑场地后,他再沿垂直υ0的方向(y轴正方向),用相同大小的力水平侧推,取g=l0m/s2,求:
,后段路面与冰块的动摩擦因数很小可忽略不计.为防止仪器室受损,又由于场地限制他只能在前一段中,逆着冰块滑来的方向与水平成370角斜向下用F=875N的力推挡冰块,如图(b)所示,此时冰块的速度为υ0=6.00m/s,在第一路段沿直线滑过4.00m后,到达两段的分界线.以分界线为y轴,冰块的运动方向为x轴建立平面直角坐标系.冰块进入光滑场地后,他再沿垂直υ0的方向(y轴正方向),用相同大小的力水平侧推,取g=l0m/s2,求:
①冰块滑到分界线时的速度大小υ1
②若仪器室D点坐标为(10.0m,5.00m);C点坐标为(10.0m,-5.00m),则此冰块能否碰到仪器室?试通过计算说明.
17. (14分)“蹦极”是冒险者的运动,质量为50kg的运动员,在一座高桥上做“蹦极”运动,他所用的弹性绳自由长度为12m,假设弹性绳中的弹力与弹性绳的伸长之间的关系遵守胡克定律,在整个运动中弹性绳不超过弹性限度,运动员从桥面下落,能达到距桥面为36m的最低点D处,运动员下落速度v与下落距离s的关系如图所示,运动员在C点时速度最大,空气阻力不计,重力加速度g取10m/s2,求:
(14分)“蹦极”是冒险者的运动,质量为50kg的运动员,在一座高桥上做“蹦极”运动,他所用的弹性绳自由长度为12m,假设弹性绳中的弹力与弹性绳的伸长之间的关系遵守胡克定律,在整个运动中弹性绳不超过弹性限度,运动员从桥面下落,能达到距桥面为36m的最低点D处,运动员下落速度v与下落距离s的关系如图所示,运动员在C点时速度最大,空气阻力不计,重力加速度g取10m/s2,求:
(1)弹性绳的劲度系数k;
(2)运动员到达D点时的加速度a的大小;
(3)运动员到达D点时,弹性绳的弹性势能EP。
解:(1)由图象知,s1=20m为平衡位置。
即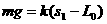 ………………………………………………………………4分
………………………………………………………………4分
代入数据解得k=62.5N/m………………………………………………………2分
(2)当s2=36m时,由牛顿第二定律得
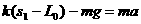 …………………………………………………………3分
…………………………………………………………3分
代入数据解得 ……………………………………………………2分
……………………………………………………2分
(3)由机械能守恒定律得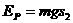 ……………………………………………3分
……………………………………………3分
代入数据解得:EP=1.8×104J……………………………………………………2分
[选做部分]
16.(1)F = (2)α =
(2)α =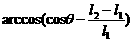
解析:(1)人由A点向B点(还处于下蹲状态时)的过程中,
根据机械能守恒得,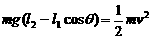
在最低点B,F-mg =
解得F =
(2)人从B点保持直立状态到达C点的过程中,
根据机械能守恒得,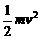 = mg l1
(1-cosα)
= mg l1
(1-cosα)
解得α =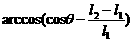
16.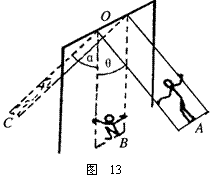 (14分)如图13是荡秋千的示意图。最初人直立站在踏板上,两绳与竖直方向的夹角均为θ,人的重心到悬点O的距离为l1;从A点向最低点B运动的过程中,人由直立状态自然下蹲,在B点人的重心到悬点O的距离为l2;在最低点处,人突然由下蹲状态变成直立状态(人的重心到悬点O的距离恢复为l1),且保持该状态到最高点C。设人的质量为m,不计踏板和绳的质量、不计一切摩擦和空气阻力,求
(14分)如图13是荡秋千的示意图。最初人直立站在踏板上,两绳与竖直方向的夹角均为θ,人的重心到悬点O的距离为l1;从A点向最低点B运动的过程中,人由直立状态自然下蹲,在B点人的重心到悬点O的距离为l2;在最低点处,人突然由下蹲状态变成直立状态(人的重心到悬点O的距离恢复为l1),且保持该状态到最高点C。设人的质量为m,不计踏板和绳的质量、不计一切摩擦和空气阻力,求
(1)人第一次到达最低点B还处于下蹲状态时,两根绳的总拉力F为多大?
(2)人第一次到达最高点C时,绳与竖直方向的夹角α为多大?(可用反三角函数表示;解答本问时可不考虑超重和失重)
15.(12分)如图,半径为R的1/4圆弧支架竖直放置,支架底AB离地的距离为2R,圆弧边缘C处有一小定滑轮,一轻绳两端系着质量分别为m1与m2的物体,挂在定滑轮两边,且m1>m2,开始时使m1、m2均静止,m1、m2可视为质点,不计一切摩擦。求:
⑴ m1从靠近滑轮处静止释放后,在紧贴着圆弧运动经过最低点A时的速度v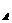 ;
;
⑵ 若m1到最低点时绳突然断开,求m1落地点离A点水平距离S;
⑶ 在满足(2)条件情况下,m2从静止起在整个过程中可以上升的最大高度H。
解析:(1)由动能定理得:
m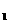 gR-m
gR-m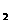 g
g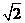 R=
R=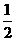 m
m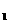
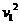 +
+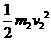 (1)
2分
(1)
2分
而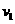 =
=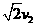 (2)
2分
(2)
2分
由(1)、(2)得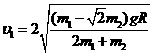 2分
2分
(2)绳断开后m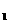 做平抛运动
做平抛运动
S=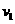 t (1分) t=
t (1分) t=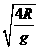 (1分) 故s=4R
(1分) 故s=4R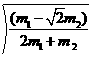 2分
2分
(3) m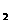 上升:
上升:

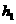 =
=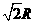 (1分), h
(1分), h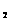 =
=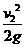 =
=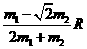 1分
1分
H=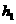 + h
+ h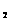 1分
1分
=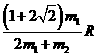 1分
1分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com