
题目列表(包括答案和解析)
[解析]由于公式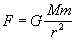 中,G、M、m都是不变的量,因此推导F和r的关系不易出错。设人造地球卫星原来的圆周运动半径为r1,所受到的地球引力为F1;当人造地球卫星的轨道半径增为r2=2r1时所受到的地球引力为F2,则:
中,G、M、m都是不变的量,因此推导F和r的关系不易出错。设人造地球卫星原来的圆周运动半径为r1,所受到的地球引力为F1;当人造地球卫星的轨道半径增为r2=2r1时所受到的地球引力为F2,则:
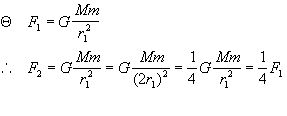
由此可知:选项(C)是正确的。
将向心力的来源公式和向心力的效果公式联系起来,可以写出下列二式:
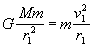 ①
①
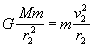 ②
②
将r2=2r1代入②式可得:
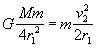 --------------------
-③
--------------------
-③
将①、③两式相除可导出: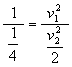
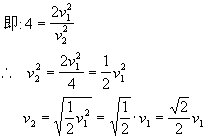
由此可知:选项(D)也是正确的。既然(D)是正确的,那么其结果不同的(A)显然是不正确的。
“卫星所需的向心力”与“地球提供的向心力”应当是一致的。既然(C)是正确的,那么与其结果不同的(B) 显然是不正确的。
[总结]由于圆周运动中同一物理的表达式可有多个形式,故在解题过程中要注意公式的正确选择,即便是一个公式,也要全面考虑这一待求物理量的所有公式,而不可‘只看一点’,不计其余的乱套乱用。
10、必须区别两个天体之间的距离L与某一天体的运行轨道半径r的不同
此处“两个天体之间的距离L”是指两天体中心之间的距离,而“r”则是指某一天体绕另一天体做匀速圆周运动的轨道半径。若轨道为椭圆时,则r是指该天体运动在所在位置时的曲率半径。一般来说,L与r并不相等,只有对在万有引力作用下围绕“中心天体”做圆周运动的“环绕天体”而言,才有L=r。这一点,对“双星”问题的求解十分重要。
“双星”系统中的两个天体共同围绕其中心天体连线上的一点而做的匀速圆周运动。不存在“环绕”与“被环绕”的关系,与地球“绕”太阳和月球“绕”地球的运转情形截然不同。因此,明确地区分“双星”之间的距离L与双星运转的轨道半径r的本质不同与内在关系就更为重要。
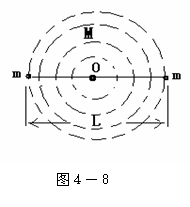
例15:天文学家经过用经过用天文望远镜的长期观测,在宇宙中发现了许多“双星”系统.所谓“双星”系统是指两个星体组成的天体组成的天体系统,其中每个星体的线度均小于两个星体之间的距离。根据对“双星”系统的光学测量确定,这两个星体中的每一星体均在该点绕二者连线上的某一点做匀速圆周运动,星体到该点的距离与星体的质量成反比。一般双星系统与其他星体距离较远,除去双星系统中两个星体之间的相互作用的万有引力外,双星系统所受其他天体的因;引力均可忽略不计。如图4-8所示。
根据对“双星”系统的光学测量确定,此双星系统中每个星体的质量均为m,两者之间的距离为L。
(1)根据天体力学理论计算该双星系统的运动周期T0.
(2)若观测到的该双星系统的实际运动周期为T,且有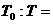
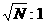 ,(N>1)。为了解释T与T0之间的差异,目前有一种流行的理论认为,在宇宙中可能存在着一种用望远镜观测不到的“暗物质”,作为一种简化的模型,我们假定认为在这两个星体的边线为直径的球体内部分布着这种暗物质,若不再考虑其他暗物质的影响,试根据这一模型理论和上述的观测结果,确定该双星系统中的这种暗物质的密度。
,(N>1)。为了解释T与T0之间的差异,目前有一种流行的理论认为,在宇宙中可能存在着一种用望远镜观测不到的“暗物质”,作为一种简化的模型,我们假定认为在这两个星体的边线为直径的球体内部分布着这种暗物质,若不再考虑其他暗物质的影响,试根据这一模型理论和上述的观测结果,确定该双星系统中的这种暗物质的密度。
[审题] “双星系统”是一种比较特殊化、理想化的天体运动的模型,求解“双星”问题时必须注意到双星之间的距离L与两球体各自作匀速圆周运动的轨道半径r的本质区别与内在关系,并建立双星的空间运动模型,然后依据万有引力定律与匀速圆周运动的规律求解即可。
[解析] (1)由于“双星”的两个星体之间的万有引力提供二者的向心力,且因二者的质量相等,故各自的运动半径均为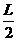 ,设各自的运行速度为v,由万有引力定律得
,设各自的运行速度为v,由万有引力定律得
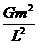 =
=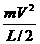 ,即得V=
,即得V=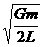 .
.
周期得公式可得,双星得运动周期为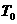 =
=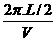 =
=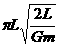
(2)此“双星”各在半径为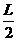 的圆形轨道上运动,由实际得天文观测知,其实际运行的周期为
的圆形轨道上运动,由实际得天文观测知,其实际运行的周期为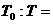
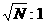 ,(N>1),即实际运动周期T<
,(N>1),即实际运动周期T<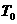 ,表明“双星’还受到其他物质的引力,且该引力必然指向圆心,由题可知,这一万有引力的来源必定时双星的范围之内均匀分布的暗物质。把这种暗物质等效于总物质集中在圆心处的星体。如图4-8所示,
,表明“双星’还受到其他物质的引力,且该引力必然指向圆心,由题可知,这一万有引力的来源必定时双星的范围之内均匀分布的暗物质。把这种暗物质等效于总物质集中在圆心处的星体。如图4-8所示,
设考虑了暗物质的作用之后,观测到的每个星体的运行速率为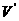 ,暗物质的总质量为M,由引力定律与圆周运动规律可得
,暗物质的总质量为M,由引力定律与圆周运动规律可得
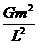 +
+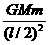 =
=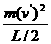 ,则
,则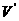 =
=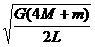 。又因T=
。又因T=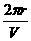 ,在半径r一定时,T与v成反比。由题意得
,在半径r一定时,T与v成反比。由题意得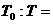
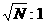 ,(N>1),则
,(N>1),则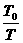 =
=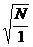 =
= ,把V=
,把V=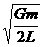 和
和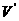 =
=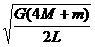 代入此式可得暗物质得总质量为M=
代入此式可得暗物质得总质量为M=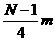 。
。
又设所求暗物质的密度为ρ,则“暗物质”质量M=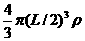 =
=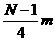 ,所以,
,所以,
ρ=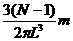 。
。
[总结] 此题中出现的“双星”“暗物质”均式很新颖的名词,是天文学的一种模型。求解“双星”问题必须把握几个要点:
①运用等效抽象的思维建立“双星”运行的空间物理情景;
②运用逻辑思维的方法,依据万有引力定律和匀速圆周运动的规律以及密度公式进行求解。
9、必须区别天体的自身半径与卫星的轨道半径的不同
宇宙中的天体各自的体积是确定的,其体积的大小可用自身半径的大小进行表述,即体积为V=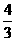 πR3 ,而这个半径R与绕该天体作匀速圆周运动的卫星(包括人造卫星)的运行轨道半径r却有本质的不同,卫星运行轨道半径r=R+h (R为所绕天体的自身半径,h为卫星距该天体表面的运行高度),卫星的轨道半径r总会大于所绕天体的自身半径R。但,当卫星在贴近所绕天体表面做近”地”飞行时,可以认为卫星的轨道半径r近似等于该天体的自身半径R,即R≈r,这一点对估算天体的质量和密度十分重要.
πR3 ,而这个半径R与绕该天体作匀速圆周运动的卫星(包括人造卫星)的运行轨道半径r却有本质的不同,卫星运行轨道半径r=R+h (R为所绕天体的自身半径,h为卫星距该天体表面的运行高度),卫星的轨道半径r总会大于所绕天体的自身半径R。但,当卫星在贴近所绕天体表面做近”地”飞行时,可以认为卫星的轨道半径r近似等于该天体的自身半径R,即R≈r,这一点对估算天体的质量和密度十分重要.
例13:已知某行星绕太阳公转的半径为r,公转周期为T万有引力常量为G,则由此可以求出 ( )
A 此行星的质量
B 太阳的质量
C 此行星的密度
D 太阳的密度
[审题]此题要求解决的问题有两个,1、求行星或太阳的质量,2 、求行星或太阳的密度.求解行星或太阳的质量而不能求出“环绕天体”的质量.在求解行星或太阳的密度时,必须综合运用密度公式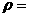
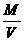 和球体积公式V=
和球体积公式V=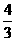 πR3,以及万有引力定律公式GMm/r2 =m4π2 r/T2,并明确给定的是行星的轨道半径r还是太阳的自身半径R,然后依据已知条件求解.
πR3,以及万有引力定律公式GMm/r2 =m4π2 r/T2,并明确给定的是行星的轨道半径r还是太阳的自身半径R,然后依据已知条件求解.
[解析]对A项.因为此行星绕太阳转动,是一个”环绕天体”而不是”中心天体”,无法用题中所给条件求出他的质量。故A选项错误。
对B选项,因为太阳是”中心天体”,依据运用万有引力定律求解天体质量的方法可得GMm/r2
=m4π2 r/T2 ,则有M=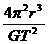 。显然依据已知条件,运用此式可以计算出太阳的质量。故B选项正确.
。显然依据已知条件,运用此式可以计算出太阳的质量。故B选项正确.
对C选项,由A选项的分析可知,不能求出此行星的质量。并且只知此行星的轨道半径r而不知此行星的自身半径R,也就无法求出行星密度.故C选项错误.。
对D选项.因为在此题中,太阳是一个”中心天体”,求太阳质量的一般思路是:由万有引力定律与匀速圆周运动规律得 GMm/r2=m4π2 r/T2------ ①
由太阳的质量密度关系得 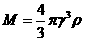 -------②
-------②
由①②两式得太阳的密度为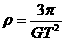 。然而,在此题中这是错误的,其错误的原因是误把题中给出的行星绕太阳运行的轨道半径r当成了太阳的自身半径R,这是极易出现的解题错误。即此处不能求出太阳的密度。故D选项错误。
。然而,在此题中这是错误的,其错误的原因是误把题中给出的行星绕太阳运行的轨道半径r当成了太阳的自身半径R,这是极易出现的解题错误。即此处不能求出太阳的密度。故D选项错误。
[总结]要运行万有引力定律和匀速圆周运动规律计算天体的质量时,必须明确研究对象是一个“中心天体”还是一个“环绕天体”,这种方法只能计算“中心天体”而不是“环绕天体”的质量,要计算天体的密度时,必须明确只能计算“中心天体”的密度,同时还必须知道此“中心天体”的自身半径R。如果把此题中的行星的轨道半径r误认为是太阳的自身半径R,则必然会导致解题的错误。
例14:假如一个作匀速圆周运动的人造地球卫星的轨道半径增大到原来的2倍,仍作匀速圆周运动,则:
(A)根据公式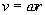 ,可知卫星运动的线速度将增大到原来的2倍。
,可知卫星运动的线速度将增大到原来的2倍。
(B)根据公式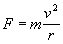 ,可知卫星所需的向心力将减小到原来的
,可知卫星所需的向心力将减小到原来的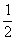 。
。
(C)根据公式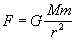 ,可知地球提供的向心力将减小到原来的
,可知地球提供的向心力将减小到原来的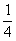 。
。
(D)根据上述(B)和(C)中给出的公式,可知卫星运动的线速度将减小到原来的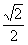 。
。
[审题]解答这个问题不应靠想象和猜测,而应通过合理的推导才能正确地选出答案。在推导的顺序上,可选择变量较少且不易出差错的选项入手。本题所提供的选项中已罗列出了各有关的公式,在解答过程时需要认真思考的是各公式使用的条件,请注意以下内容:
8、必须区别“赤道物体”与“同步卫星”以及“近地卫星”的运动规律不同
地球同步卫星运行在赤道上空的“天上”,与地球保持相对静止,总是位于赤道的正上空,其轨道叫地球静止轨道.通信卫星、广播卫星、气象卫星、预警卫星等采用这样的轨道极为有利一颗静止卫星可以覆盖地球大约40%的面积,若在此轨道上均匀分布3颗卫星,即可实现全球通信或预警.为了卫星之间不互相千扰,大约30左右才能放置1颗,这样地球的同步卫星只能有120颗.可见,空间位置也是一种资源。
其绕地球做匀速圆周运动所需的向心力完全由万有引力提供.即 。此同步卫星与其内部的物体均处于完全失重状态。地球同步卫星具有以下特点:
。此同步卫星与其内部的物体均处于完全失重状态。地球同步卫星具有以下特点:
轨道取向一定: 运行轨道平面与地球赤道平面共面.
运行方向一定: 运行方向一定与地球的自转方向相同.
运行周期一定: 与地球的自转周期相同,T=86400s,
位置高度一定: 所在地球赤道正上方高h=36000km处
运行速率一定: v=3.1km/s,约为第一宇宙速度的0.39倍.
运行角速度一定: 与地球自转角速度相同,ω=7.3 ×10-5rad/s。
地球同步卫星相对地面来说是静止的。
地球赤道上的物体,静止在地球赤道的”地上”与地球相对静止,随地球的自转绕地轴做匀速圆周运动.地球赤道上的物体所受地球的万有引力,其中的一个力提供随地球自转所做圆周运动的向心力,产生向心加速度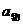 ,引力产生的另一效果分力为重力,有
,引力产生的另一效果分力为重力,有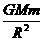 -mg=m
-mg=m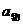 (其中R为地球半径)。
(其中R为地球半径)。
近地卫星的轨道高度、运行速度、角速度、周期等,均与同步卫星不同,更与“赤道上的物体”不可相提并论。
“赤道上的物体”与“地球同步卫星”的相同之处是:二者具有与地球自转相同的运转周期和运转角速度,始终与地球保持相对静止状态,共同绕地轴做匀速圆周运动;“近地卫星”与“地球同步卫星”的相同之处是:二者所需要量的向心力均是完全由地球的万有引力提供。
例11: (2004年北京模拟) 设地球半径为R,地球自转周期为T,地球同步卫星距赤道地面的高度为h,质量为m,试求此卫星处在同步轨道上运行时与处在赤道地面上静止时的:①线速度之比, ②向心加速度之比,③所需向心力之比。
[审题] 此题的求解关键在于明确地球同步卫星与地球赤道上物体的不同特点及其各自遵守的规律.必须明确一个在“天上”,一个在“地上”,其所受万有引力产生的效果不同,必须依据万有引力定律与匀速圆周运动的规律求解。
[解析]由于卫星在同步轨道运行时与处在赤道平面上静止时,具有相同的运转角速度,则可得
① 二者的线速度之比为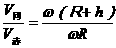 =
=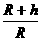 。
。
②二者的向心速度之比为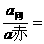 ω2(R+h)/ω2.R=
ω2(R+h)/ω2.R=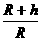 。
。
③二者所需要的向心力之比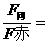 mω2(R+h)/mω2.R=
mω2(R+h)/mω2.R=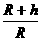 。
。
显然,由以上解答可知,此三个比值均为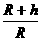 ,又由于地球同步距地面高度为h=3。6×106m,地球半径为R=6.4×106m.故此比值为
,又由于地球同步距地面高度为h=3。6×106m,地球半径为R=6.4×106m.故此比值为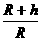 =
=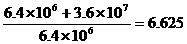 。
。
[总结]运用万有引力定律解题时,必须明确地区分研究对象是静止在”地面上”的物体还是运行在轨道上(天上)的卫星?是地球的万有引力是完全提供向心力还是同时又使物体产生了重力?这一点就是此类题目的求解关键。此外,还要特别注意到同步卫星与地球赤道上的物体具有相同的运行角速度和运行周期。
例12:设同步卫星离地心距离为r,运行速率为v1,加速度为al,地球赤道上的物体随地球自转的向心加速度为a2,第一宇宙速度为v2,地球半径为R,下列关系中正确的有( )。
A、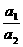 =
=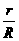 B、
B、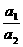 =
=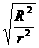
C、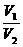 =
=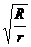 D、
D、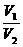 =R/r
[审题] 此题的研究对象有三个:一是地球同步卫星;二是静止在赤道地面上的物体;三是与第一宇宙速度相对应的近地卫星;
=R/r
[审题] 此题的研究对象有三个:一是地球同步卫星;二是静止在赤道地面上的物体;三是与第一宇宙速度相对应的近地卫星;
题中需要解析对比的物理量有两组:一是同步卫星的向心加速度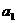 和赤道上的静止物体的自转向心加速度
和赤道上的静止物体的自转向心加速度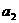 ;二是同步卫星的运行速度
;二是同步卫星的运行速度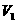 和第一宇宙速度
和第一宇宙速度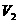 。必须明确求解卫星向心加速度的公式有多个,如,a=
。必须明确求解卫星向心加速度的公式有多个,如,a= 、a=
、a=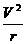 、a=
、a=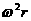 等等;求解卫星运行速度的公式也有多个,如,v =
等等;求解卫星运行速度的公式也有多个,如,v =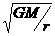 、
、 V=
V=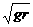 、V=
、V= 等等。只要明确同步卫星与赤道地面上的物体产生向心加速度的原因,区别同步卫星的运行速度与第一宇宙速度的不同,依据题中给定的已知条件,(卫星的轨道半径r和地球的半径R),再正确选择公式解答,即可得到正确答案。
等等。只要明确同步卫星与赤道地面上的物体产生向心加速度的原因,区别同步卫星的运行速度与第一宇宙速度的不同,依据题中给定的已知条件,(卫星的轨道半径r和地球的半径R),再正确选择公式解答,即可得到正确答案。
[解析] 对选项A,由于同步卫星的向心加速度与赤道地面上的物体向心加速度的产生原因不同,对同步卫星是万有引力提供了向心力,
则: =m
=m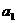 ,-
---------------①
,-
---------------①
对于赤道物体: 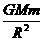 -N=m
-N=m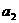 -----------------------②(式中的N是地面对物体的支持力)
-----------------------②(式中的N是地面对物体的支持力)
此处讨论的就是地球的自转,故,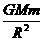 ≠mg,
≠mg,
而是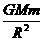 =
mg+m
=
mg+m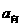 .①②显然正确,但无法用来求得
.①②显然正确,但无法用来求得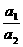 的比值。
的比值。
又因为,同步卫星与赤道地面上的物体具有相同的角速度,则:
对同步卫星,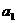 =
=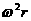 ;
;
对赤道地面上的物体,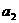 =
=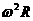 ,由此二式可得
,由此二式可得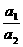 =
=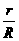 ,故选项A正确。
,故选项A正确。
对选项B,常见这样的解法:因同步卫星在高空轨道,则 =m
=m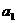 得,
得,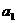 =
= ;
;
对赤道地面上的物体,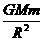 = m
= m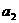 得,
得,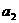 =
=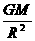 。
。
以上二式相比得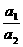 =
=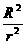 。其实,这是错误的,----―――这是一种典型的、常见的错误。其原因是错误的对“赤道地面上的物体”运用了
。其实,这是错误的,----―――这是一种典型的、常见的错误。其原因是错误的对“赤道地面上的物体”运用了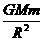 = m
= m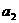 的关系。实际上,“赤道地面上的物体”是在‘地’上,其随地球自转而需要的向心力并非完全由万有引力提供,而是由万有引力与地面的支持力的合力提供,即
的关系。实际上,“赤道地面上的物体”是在‘地’上,其随地球自转而需要的向心力并非完全由万有引力提供,而是由万有引力与地面的支持力的合力提供,即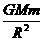 = m
= m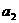 不成立,只有
不成立,只有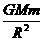 =
mg+m
=
mg+m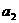 才是正确的。
才是正确的。
同步卫星是在“天”上,其需要的向心力完全由万有引力提供,式 =m
=m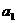 是成立的。
是成立的。
显然,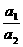 =
=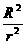 是完全错误的,故选项B错误。
是完全错误的,故选项B错误。
对选项C,同步卫星需要的向心力完全由万有引力提供,则, =
=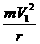 ,所以,
,所以,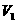 =
=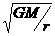 。
。
对于第一宇宙速度,有,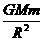
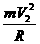 ,则
,则 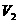 =
=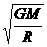
二式相比得: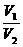 =
=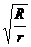 。故选项C正确。
。故选项C正确。
对选项D,因为第一宇宙速度是卫星的最小发射速度,也是卫星的环绕速度,但不是“赤道地面上的物体”的自转速度。如果忽视了此点而误认为“同步卫星”与“赤道地面上的物体”具有相同的角速度,则必然会由公式V= 得出:
得出:
对同步卫星,V1=
对赤道地面上的物体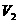 =
=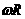
二式相比可得: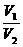 =
=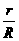 。此比值
。此比值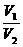 =
=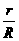 的结论对于“同步卫星”和“赤道地面上的物体”的速度之比无疑是正确的,但是选项D中的
的结论对于“同步卫星”和“赤道地面上的物体”的速度之比无疑是正确的,但是选项D中的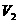 是第一宇宙速度而不是“赤道地面上的物体”的自转速度。故选项D错误。
是第一宇宙速度而不是“赤道地面上的物体”的自转速度。故选项D错误。
[总结] 求解此题的关键有三点:
①、在求解“同步卫星”与“赤道地面上的物体”的向心加速度的比例关系时应依据二者角速度相同的特点,运用公式a=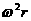 而不能运用公式a=
而不能运用公式a= 。
。
②在求解“同步卫星”与“赤道地面上的物体”的线速度比例关系时,仍要依据二者角速度相同的特点,运用公式V= 而不能运用公式v =
而不能运用公式v =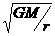 ;
;
③、在求解“同步卫星”运行速度与第一宇宙速度的比例关系时,因均是由万有引力提供向心力,故要运用公式v =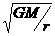 而不能运用公式V=
而不能运用公式V= 或V=
或V=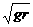 。很显然,此处的公式选择是至关重要的。
。很显然,此处的公式选择是至关重要的。
7、必须区别赤道轨道卫星、极地轨道卫星与一般轨道卫星的不同
人造地球卫星从轨道取向上一般分为三类:赤道轨道、极地轨道和一般轨道。
所谓赤道轨道卫星,是指这种卫星的轨道处在地球赤道的平面之内,卫星距赤道地面具有特定的高度,其运行速度由公式 v =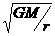 可求得。而在实际当中只有处在36000km高空的赤道轨道上,且只有与地球自转方向相同的卫星才能与地球相对静止,称之为“同步卫星”,如图4-7所示。如果其转向与地球自转反向,则就不能称之为“同步卫星”了。另外,发射地球同步卫星时,为了节省能量,其发射地点应尽量靠近赤道,以借助地球的自转线速度。地球同步卫星具有“轨道不偏不倚”、“高度不高不低”、 “速度不快不慢”的六不特性。如图4-7所示
。
可求得。而在实际当中只有处在36000km高空的赤道轨道上,且只有与地球自转方向相同的卫星才能与地球相对静止,称之为“同步卫星”,如图4-7所示。如果其转向与地球自转反向,则就不能称之为“同步卫星”了。另外,发射地球同步卫星时,为了节省能量,其发射地点应尽量靠近赤道,以借助地球的自转线速度。地球同步卫星具有“轨道不偏不倚”、“高度不高不低”、 “速度不快不慢”的六不特性。如图4-7所示
。
所谓极地轨道卫星,是指卫星的轨道平面始终与太阳保持相对固定的取向.其轨道平面与地球赤道平面的夹角接近90度。
卫星可在极地附近通过,故又称为近极地太阳同步卫星。如图4-7所示.这种卫星由于与地球之间有相对运动,可以观测,拍摄地球上任一部位的空中,地面的资料。1999年5月10日我国”一箭双星”发射的”风云一号”与”风云二号”气象卫星中的”风云一号”就是这种极地轨道卫星。
所谓一般轨道卫星是指轨道平面不与某一经线平面重合(赤道平面除外)的人造地球卫星。
以上三种轨道卫星共同特点是轨道中心必须与地心重合,是以地心为圆心的”同心圆”.,没有与地球经线圈共面的轨道(赤道平面除外)。
例10: (2000年全国春季高考)可以发射一颗这样的人造地球卫星,使其圆轨道( )
A 与地球表面上某一纬度线(赤道除外)是共面的同心圆
B 与地球表面上某一经度线所决定的圆是共面的
C 与地球表面上的赤道线是共面同心圆,而且相对地球表面是静止的
D与地球表面上的赤道线是共面同心圆, 但卫星相对地球表面是运动的
[审题]此题重在判断人造地球卫星的轨道取向与地球的经度线平面,纬度线平面,赤道平面的关系.在辨析,判断时必须明确以下几点:
1 作匀速圆周运动的卫星必定是无动力飞行,其轨道中心必然在地球中心。
2 人造地球卫星的轨道有三种:赤道轨道,极地轨道,一般轨道。
3 地球同步卫星的运行轨道与位置高度等方面的特点。
只要依据以上几方面的特点即可辨析选择出正确答案。
[解析]
对A选项,人造地球卫星运行时,是地球对它的万有引力提供向心力,而此向心力的方向必定指向地心,即所有无动力飞行的卫星轨道的圆心一定与地球中心重合,不能是地轴上(除地心之外)的某一点。故A项错误.
对B项,由于地球绕地轴在自转,所以卫星的轨道平面不可能与经度线所决定的平面共面.故B项是错误的。
对C项,相对地球表面静止的卫星就是”同步卫星”,它必须处在赤道圈平面,且距离赤道地面有确定的高度,高度H=36000千米,其运行速度必须是V=3.1km/s.运行周期与地球自转周期相同.故C项正确。
对D选项,如果卫星所在的高度低于或高于h=36000km时,便不再是地球同步卫星。虽然还可以使轨道处于地球赤道平面之内,但由于运转的周期与地球自转的周期不会相同,也就会相对地面运动.这种卫星就是地球赤道轨道卫星,但不是地球同步卫星,故D项正确。
[总结]这是一个关于人造地球卫星运行轨道的问题,也是一个“高起点”、“低落点”的题目,符合高考能力考察的命题思想.但是现行高中物理教科书中不会介绍的很具体,对于这一类卫星轨道问题,也只能从卫星的向心力来源、运行轨道的取向以及同步卫星的特点规律等方面分析判断.此处必须明确只有万有引力提供向心力.
6、必须区别由万有引力、重力、向心力构成的三个等量关系式的不同
针对天体(行星,卫星)和人造地球卫星的运行问题(包括线速度、周期、高度 ),可以看作匀速圆周运动,从而运用万有引力定律。这类“天上”的物体作匀速圆周运动的向心力仅由万有引力提供。对于地面物体,其重力由万有引力产生,若忽略随地球自转的影响,则其重力等于万有引力。由于 “天上”的物体(如行星、卫星)与地面上的物体虽然遵守相同的牛顿力学定律,但也有本质的区别,通常在解决卫星问题时要特别注重以下三个等量关系:
若万有引力提供向心力,则有 GMm/r2 =ma向
若重力提供向心力, 则有 mg= ma向
若万有引力等于重力, 则有 GMm/r2 =mg
以上三式不仅表现形式有异,而且其物理意义更是各有不同,必须注意区别辨析。同时因向心加速度a向又具有多种不同的形式,如a向 =v2/r =ω2r= 4π2 r/T2 ……则可以得以下几组公式:
(1)由 GMm/r2 =ma向 得
GMm/r2 =ma向→a向=GM/r2→a向∝1/r2。
GMm/r2 =m v2/r→v =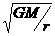 →v∝1/
→v∝1/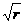
GMm/r2 =mω2r→ω=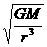 →ω∝1/
→ω∝1/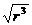
GMm/r2=m4πT 2 r/T2→T=2π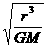 →T∝
→T∝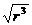
对于以上各式,“中心天体”(如地球)一定,则其质量M是一定的。因此“环绕天体”(卫星)绕其做匀速圆周运动的向心加速度a向、运行速度v、运行角速度ω、运行周期T仅与距离r有关。即以上各量仅由距离r即可得出,故以上各式可称之为 “决定式”。这组决定式适应于用 “G、M、r”表示待求物理量的题目。
(2)由 mg= ma向可得
mg= ma向→a向=g
mg= m v2/r→v=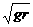 →v∝
→v∝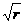
mg= mω2r→ω=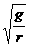 →ω∝1/
→ω∝1/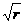
mg= m4π2 r/T2→ T=2π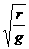 →T∝
→T∝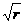
以上各式之中,作匀速圆周运动的物体(如卫星)的运行速度v、角速度ω 、周期T由距离r和重力加速度g共同决定。其中的“g“也是一个随距离r而变化的变量,而不能认为是一个恒量。这组公式是由GMm/r2 =mg的代换关系得到的,一般适应于已知“g、r”而不知“G、M”的题目。
(3)由GMm/r2 =mg 得,对于地面上的物体可由r=Ro (Ro为地球半径),g=go(go为地球表面的重力加速度)若忽略地球自转,则有GMm/ R2o =m go。即GM= go R2o--此即所谓的“黄金代换”,可用来作为“G、M”与“go 、Ro”之间的等量代换。----------这一关系在解题中经常用到。
例9:(2006年五市区联考)设有两颗人造地球卫星的质量之比为m1:m2 =1:2,其运行轨道半径之比为R1:R2 =3:1,试求此两颗卫星运行的:
①线速度之比,②角速度之比,③周期之比,④向心加速度之比。
[审题]根据此题要求求解的四个“比”值,其给定的已知条件中的“m1:m2 =1:2”是无用的“干扰项”,只须运用已知条件“R1:R2 =3:1”即可求解,但是必须注意所用公式。因为只是已知两颗卫星的轨道半径的比例关系,故而求解时也只能选用上面(1)中的“决定式”,而不能选用(2)中的公式。
[解析]人造地球卫星在轨道上运行时,所需要的向心力等于地球的万有引力,由F引=F向可得,
① GMm/r2 =m v2/r,则v =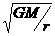 所以,
所以,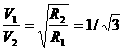 。
。
如果此处运用了v=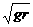 ,而认为v∝
,而认为v∝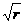 ,则可得到
,则可得到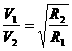 =
=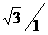 ,显然这是错误的。因为对于这两颗卫星而言其公式v=
,显然这是错误的。因为对于这两颗卫星而言其公式v=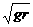 中的“g”是不同的。
中的“g”是不同的。
② 因为GMm/r2 =mω2r,有ω=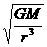 ,故,
,故,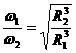
 =
=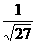 ;如果此处运用公式ω=
;如果此处运用公式ω=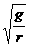 而认为ω∝1/
而认为ω∝1/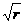 ,则可得,
,则可得,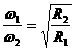 =
=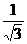 ,显然也是错误的。其原因仍是忘掉了式中“g” 的不同。
,显然也是错误的。其原因仍是忘掉了式中“g” 的不同。
③ 因为GMm/r2 =m4π2 r/T2 ,则,T=2π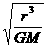 ,故有
,故有 =
=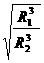 =
=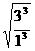 =
=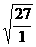 。如果此处运用了T=2π
。如果此处运用了T=2π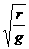 而认为T∝
而认为T∝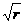 ,则得
,则得 =
=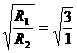 ,显然也是错误的。其原因仍是忘掉了式中“g” 的不同。
,显然也是错误的。其原因仍是忘掉了式中“g” 的不同。
 ④ GMm/r2=ma向,则a向=GM/r2 故有,
④ GMm/r2=ma向,则a向=GM/r2 故有,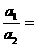
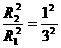 =1/9。如果此处运用了a向=g而认为a向轨道半径无关,则得
=1/9。如果此处运用了a向=g而认为a向轨道半径无关,则得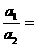
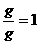 ,必然错误,其原因仍是忘掉了式中“g”的不同。
,必然错误,其原因仍是忘掉了式中“g”的不同。
[总结] 在求解天体(如,行星、卫星等)的圆周运动时,由于圆周运动的特点以及“黄金代换”关系(GM=go R2o)的存在,会使得圆周运动中的同一个物理量有多种不同形式的表达式。如,对于线速度就有v =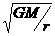 、v=
、v=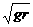 、V=ωr、V=2πr/T………等多种形式。在解题时除了要明确这些公式的不同意义和不同条件之外,还必须依据题意有针对性的选取运用,同时还必须牢记“黄金代换”关系式GM=go R2o的重要性。
、V=ωr、V=2πr/T………等多种形式。在解题时除了要明确这些公式的不同意义和不同条件之外,还必须依据题意有针对性的选取运用,同时还必须牢记“黄金代换”关系式GM=go R2o的重要性。
5、必须区别卫星的运行速度与发射速度的不同
对于人造地球卫星,由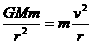 可得v=
可得v=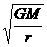 ,这个速度指的是人造地球卫星在轨道上稳定运行的速度。其大小仅随轨道半径r的增大而减小,与卫星的质量、形状等因素无关。只要卫星能运行在半径为r`的轨道上,其运行的速度就必须是而且也只能是 v=
,这个速度指的是人造地球卫星在轨道上稳定运行的速度。其大小仅随轨道半径r的增大而减小,与卫星的质量、形状等因素无关。只要卫星能运行在半径为r`的轨道上,其运行的速度就必须是而且也只能是 v=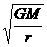 ,此式是人造地球卫星稳定运行速度的决定公式。
,此式是人造地球卫星稳定运行速度的决定公式。
人造地球卫星在圆轨道上的运行速度是随着高度的增大而减小的,由于人造地球卫星的发射过程中必须克服地球引力做功,从而增大了卫星的引力势能,故要将卫星发射到距地球越远的轨道,需要克服地球的引力做功就越多,在地面上需要的发射速度就要越大。其发射速度的具体数值由预定轨道的高度决定,在第一宇宙速度(7.9 km/s)和第二宇宙速度(11. 2 km/s)之间取值。要明确三个宇宙速度均指发射速度。而第一宇宙速度(7.9 km/s)既是卫星的最小发射速度又是卫星的最大运行速度。
人造地球卫星的三个发射速度分别是:
第一宇宙速度(环绕速度):v=7.9千米/秒;(地球卫星的最小发射速度)
第二宇宙速度(脱离速度):v=11.2千米/秒;(卫星挣脱地球束缚的最小发射速度)
第三宇宙速度(逃逸速度):v=16.7千米/秒。(卫星挣脱太阳束缚的最小发射速度)
例8:1999年5月10日,我国成功地发射了“一箭双星”,将“风云一号”气象卫星和“实验五号”科学实验卫星送入离地面高870km的轨道。这颗卫星的运行速度为( )
A、7.9km/s B、11.2 km/s
C、7.4 km/s D、3.1 km/s
[审题] 题目中叙述的是人造地球卫星的“发射”与“运行”,考查的是人造地球卫星的“发射速度”与“运行速度”的物理意义。此题给出的四个速度中有三个具有特定的物理意义。只要明确这三个特殊速度的物理意义,此题求解也就十分容易。此题可有两种不同的解法,一是,根据题中的三个特殊速度而作出判断;二是根据题中给出的卫星高度h=870km和其他的常量计算出此卫星的实际运行速度,即可选出正确答案。
[解析]
(方法一)判断选定法
对选项A,v=7.9km/s的速度是地球的第一宇宙速度,是发射速度。以此速度发射的人造地球卫星会以v=7.9km/s的速度环绕地球低轨道运行。其轨道半径近似等于地球半径,即r≈R地,不会处在h=870km的轨道上。故A选项错误。
对选项B,v=11.2km/s是地球的第二宇宙速度,是发射速度,以此速度发射的人造地球卫星会脱离地球的引力范围,飞到距地球的“无限远处”(在理论上此卫星的轨道半径r=∞,其绕地球运行速度v=0),不会稳定运行在h =870km的轨道上,故B选项错误。
对选项C,v=7.4km/s<7.9km/s(第一宇宙速度),则肯定是卫星的运行速度。但是否以此速度运行的卫星就一定处在h=870km的轨道上?还要计算判定。然而,由于又在“D选项中”有v=3.1km/s是地球同步卫星运行速度,而同步卫星的轨道高度是36000km而不是870km。故运用排除法即可得知C选项正确。
对选项D,v=3.1km/s必然是同步卫星的运行速度,而同步卫星的轨道高度是距地球赤道地面36000km ,而不是870km。故D选项错误。
(方法二)计算选定法
由于地球的万有引力提供了人造地球卫星的向心力,故得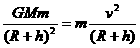 ,则有v=
,则有v=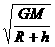 ,代入引力常量G=6.67×10-11 Nm2/Kg2,地球质量M=5.98×1024Kg,地球半径R=6400km和卫星的轨道高度h=870km。可得v=7.4km/s,即此卫星的运行速度为7.4km/s。故C选项正确。
,代入引力常量G=6.67×10-11 Nm2/Kg2,地球质量M=5.98×1024Kg,地球半径R=6400km和卫星的轨道高度h=870km。可得v=7.4km/s,即此卫星的运行速度为7.4km/s。故C选项正确。
[总结] 以上两种方法相比,显然是前一种“判断选定法”更为简捷方便,但是要熟知题中给的各个速度的含义,只要排除不合理的答案即可得到正确答案。如果要运用计算选定法,则需要进行繁杂的数值计算,稍有不慎不仅会影响解题速度甚至还会导致错误。故而注重选择题的解答技巧十分重要。
[解析] 物体的重力来自万有引力,所以离火星表面R火高处:m =GM火·m/(2R火)2
=GM火·m/(2R火)2
 =
=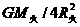 。离地对表面R地高处:m
。离地对表面R地高处:m =GM地·m/(2R地)2,
=GM地·m/(2R地)2, =
=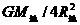
∴ /
/ =
= ·
·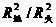 =P/q2
=P/q2
[总结] 由于引力定律公式中只有乘法与除法,故可以运用比例法进行求解。对星球表面上空某处的重力加速度公式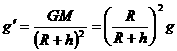 ,也可以这样理解:g′和星球质量成正比和该处到球心距离的平方成反比。
,也可以这样理解:g′和星球质量成正比和该处到球心距离的平方成反比。
4、必须区别天体系统中‘中心天体’与‘环绕天体’的不同
对于天体质量的测量,常常是运用万有引力定律并通过观测天体的运行周期T和轨道半径r(必须明确天体的运行周期T和轨道半径r是研究卫星问题中的两个关键物理量),把天体或卫星的椭圆轨道运动近似视为匀速圆周运动,然后求解。但是必须区别天体系统中‘中心天体’与‘环绕天体’的不同。
所谓‘中心天体’是指位于圆周轨道中心的天体,一般是质量相对较大的天体;如,恒星、行星等等。所谓‘环绕天体’是指绕着‘中心天体’做圆周运动的天体或者卫星以及人造卫星,一般是质量相对较小的天体或卫星。此种方法只能用来测定‘中心天体’的质量,而无法用来测定‘环绕天体’的质量。这是解题时必须注意的。
(1)根据天体表面上物体的重力近似等于物体所受的万有引力,由天体表面上的重力加速度和天体的半径求天体的质量,其公式推证过程是:
由mg=G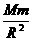 得
得
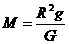 .(式中M、g、R分别表示天体的质量、天体表面的重力加速度和天体的半径.)
.(式中M、g、R分别表示天体的质量、天体表面的重力加速度和天体的半径.)
(2)根据绕中心天体运动的卫星的运行周期和轨道半径,求中心天体的质量
卫星绕中心天体运动的向心力由中心天体对卫星的万有引力提供,利用牛顿第二定律得
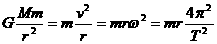
若已知卫星的轨道半径r和卫星的运行周期T、角速度 或线速度v,可求得中心天体的质量为
或线速度v,可求得中心天体的质量为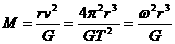
例7:已知引力常量G和以下各组数据,能够计算出地球质量的是:
地球绕太阳运行的周期和地球与太阳间的距离
月球绕地球运行的周期和月球与地球间的距离
人造地球卫星在地面附近处绕行的速度与周期
若不考虑地球的自转,已知地球的半径与地面的重力加速度
[审题]此题中的目的是求解‘地球’的质量,其关键在于题中所给四个情景中“地球”是否是一个‘中心天体’.若地球是一个‘中心天体’,则可在题中所给的四个情景中找到以地球为‘中心天体’、以‘月球’或‘卫星’为运‘环绕天体’的系统,再运用万有引力定律和匀速圆周运动的规律联合求解。此外,还要注意到每一个选项中给定的两个物理量能否用得上,只有做好这样的分析判断之后,解题才能事半功倍。解此题关键是要把式中各字母的含义弄清楚,要区分天体半径和天体圆周运动的轨道半径.
[解析] 对A选项。此选项之中“地球绕太阳运转”,给定的条件是”地球绕太阳的运转周期”和”地球与太阳之间的距离”。显然此处的”中心天体”是太阳而非地球,地球是一个”环绕天体”, 而已知的是地球绕太阳运行的周期和地球的轨道半径,只能求出太阳的质量,因此无法计算出地球的质量。故A选项错误.
对B选项。在此选项中,月球绕地球运转,月球是“环绕天体”,而地球是“中心天体”,且已知月球绕地球的运转周期T和月球与地球之间的距离r,由万有引力定律与匀速圆周运动的规律可得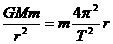 ,故有地球质量为M=
,故有地球质量为M=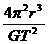 ,显然,式中的各量均为已知量,即地球质量由此式可计算出来。故B选项正确。
,显然,式中的各量均为已知量,即地球质量由此式可计算出来。故B选项正确。
对C选项。在此项中人造地球卫星是“环绕天体“,而地球则是中心天体,又已知人造地球卫星的运行速度v和运动周期T,由万有引力定律与匀速圆周运动规律可得
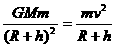 和
和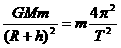 ,又因为此人造地球卫星是”近地“卫星,则h<<R,可视为h≈0,必有R+h≈R,则以上两式可分别化为
,又因为此人造地球卫星是”近地“卫星,则h<<R,可视为h≈0,必有R+h≈R,则以上两式可分别化为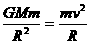 -----① 和
-----① 和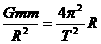 -----②,
-----②,
又由于v=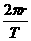 ,代入①式(当然也可以代入②式)可得,地球的质量为M=
,代入①式(当然也可以代入②式)可得,地球的质量为M=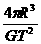 。显然此式中的量均为已知。即可由此式计算出地球质量。故C选项正确。
。显然此式中的量均为已知。即可由此式计算出地球质量。故C选项正确。
对D选项。可以运用虚拟物体法计算地球的质量。假设有一个在地面上静止的物体,对其运用万有引力定律可得: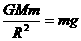 ,则M=
,则M=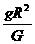 。其中的g为地面上的重力加速度,R为地球半径,均为已知,可以由此计算出地球质量。故D选项正确。
。其中的g为地面上的重力加速度,R为地球半径,均为已知,可以由此计算出地球质量。故D选项正确。
[总结] 对于天体的质量是通过测量计算得到的,而不是通过称量获得。首先要明确,这种方法只能用来计算“中心天体”的质量,而不能计算“环绕天体”的质量。其次还必须明确利用题中所给的天文数据能否计算出被测天体的质量。只有满足这两方面面的要求,才可以运用万有引力定律和匀速圆周运动的规律计算求得天体的质量。
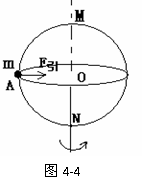
3、必须区别地面物体的万有引力与重力以及向心力的不同
(1)地球对地面物体的万有引力:地面上的物体所受地球引力的大小均由万有引力定律的公式F=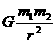 决定,其方向总是指向地心。
决定,其方向总是指向地心。
(2)地面物体所受的重力:
处在地面上的物体所受的重力是因地球的吸引而产生的,其大小为mg,方向竖直向下(绝不可以说为“垂直向下”和“指向地心”)。
地面上同一物体在地球上不同纬度处的的重力是不同的。在地球的两极上最大,在地球赤道上最小,随着位置从赤道到两极的移动而逐渐增大-----这种现象不是‘超重’,应该与‘超重’现象严格区别开来。
以地球赤道上的物体为例,如图4-4所示,质量为m的物体受到的引力为F=GMm/R2 ,因此物体与地球一起转动,即以地心为圆心,以地球半径为半径做匀速圆周运动,角速度即与地球的自转角速度相同,所需要的向心力为 F向=mωR2 =mR4π2/T2.因地球自转周期较大,F向必然很小,通常可忽略,故物体在地球两极M或N上时其重力等于受到的万有引力。
一般说来,同一物体的重力随所在纬度的变化而发生的变化很小,
有时可以近似认为重力等于万有引力,即mg=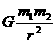 。
。
在任何星体表面上的物体所受的重力均是mg=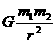 ,而物体在距星体表面高度为h处的重力为mg’=Gm1m2/(r+h)2
,而物体在距星体表面高度为h处的重力为mg’=Gm1m2/(r+h)2
 (3)地面物体随地球自转所需的向心力:
(3)地面物体随地球自转所需的向心力:
由于地球的自转,处于地球上的物体均随地球的自转而绕地轴做匀速圆周运动,所需向心力由万有引力提供,大小是F向=mω2r=mr4π2/T2(ω是地球自转角速度,r是物体与地轴间的距离,T是地球的自转周期),其方向是垂直并指向地轴。对于同一物体,这一向心力在赤道时最大,F大=mω2R(R是地球半径);在两极时最小,F小=0。
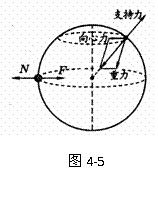
因地球自转,地球赤道上的物体也会随着一起绕地轴做圆周运动,这时物体受地球对物体的万有引力和地面的支持力作用,物体做圆周运动的向心力是由这两个力的合力提供,受力分析如图4-5所示.
实际上,物体受到的万有引力产生了两个效果,一个效果是维持物体做圆周运动,另一个效果是对地面产生了压力的作用,所以可以将万有引力分解为两个分力:一个分力就是物体做圆周运动的向心力,另一个分力就是重力,如图4-5所示.这个重力与地面对物体的支持力是一对平衡力.在赤道上时这些力在一条直线上.
当在赤道上的物体随地球自转做圆周运动时,由万有引力定律和牛顿第二定
律可得其动力学关系为 ,式中R、M、
,式中R、M、 、T分别为地球的半径、质量、自转角速度以及自转周期。
、T分别为地球的半径、质量、自转角速度以及自转周期。
当赤道上的物体“飘”起来时,必须有地面对物体的支持力等于零,即N=0,这时物体做圆周运动的向心力完全由地球对物体的万有引力提供.由此可得赤道上的物体“飘”起来的条件是:由地球对物体的万有引力提供向心力。以上的分析对其它的自转天体也是同样适用的。
(4)万有引力、重力、向心力三者间的关系:
地面物体随地球自转所需向心力F向=mω2r=mr4π2/T由万有引力F引=GMm/R2提供,F向是F引的一个分力,引力F引的另一个分力才是物体的重力mg,引力F引是向心力F向和重力mg的合力,三者符合力的平行四边形定则,大小关系是F引≥mg>F向。
例4:已知地球半径R=6.37×106m.地球质量M=5.98×1024Kg,万有引力常量G=6.67×10-11 Nm2/Kg2.试求挂在赤道附近处弹簧秤下的质量m=1Kg的物体对弹簧秤的拉力多大?
[审题]对物体受力分析如图4-6所示,弹簧秤对物体竖直向上的拉力和地球对物体竖直向下的万有引力的合力提供了物体随地球自转而做匀速圆周运动的向心力。
 [解析]在赤道附近处的质量m=1Kg的物体所受地球的万有引力为
[解析]在赤道附近处的质量m=1Kg的物体所受地球的万有引力为
F=GMm/R2=6.67×10-11×5.98×1024×1/ (6.37×106)2 N=9.830N
此物体在赤道所需向心力为 F向=mω2R=mR4π2/T2=
1×(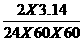 )2×6.37×106 N=0.0337 N。
)2×6.37×106 N=0.0337 N。
此物体在赤道所受到的弹簧秤拉力为F拉=F-F向=(9.830-0.0337)N
=9.796N。
由牛顿第三定律可知,物体对弹簧秤的拉力为F拉=9.796N。亦即物体所受到的重力也是9.796N。
[总结]由计算可知,引力F=9.830N远大于向心力F向=0.0337 N,而物体所受重力9.796N与物体所受的万有引力F=9.830N相差很小,因而一般情况下可认为重力的大小等于万有引力的大小。但应该切记两点:①重力一般不等于万有引力,仅在地球的两极时才可有大小相等、方向相同,但重力与万有引力仍是不同的两个概念。②不能因为物体随地球自转所需要的向心力很小而混淆了万有引力、重力、向心力的本质区别。
例5:地球赤道上的物体重力加速度为g,物体在赤道上随地球自转的向心加速度为a,要使赤道上的物体“飘”起来,则地球转动的角速度应为原来的( ) 倍
A.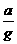 B.
B.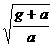 C.
C.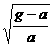 D.
D. 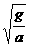
[审题]依据牛顿第二定律和万有引力定律,以赤道上的物体“飘”起来的动力学本质为‘切入口,’即可求出地球转动的角速度。
[解析]设地球原来自转的角速度为 ,用F表示地球对赤道上的物体的万有引力, N表示地面对物体的支持力,由牛顿第二定律得
,用F表示地球对赤道上的物体的万有引力, N表示地面对物体的支持力,由牛顿第二定律得 ①
①
由于物体受到的支持力与物体的重力是一对平衡力,所以有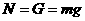 ②
②
当赤道上的物体“飘”起来时,只有万有引力提供向心力,设此时地球转动的角速度为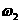 ,有
,有 ③
③
联立①、②、③三式可得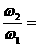
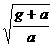 ,所以正确答案为B选项。
,所以正确答案为B选项。
[总结]当赤道上的物体“飘”起来时,是一种物体、地球之间接触与脱离的临界状态,地球对物体的支持力为零,只有万有引力完全提供向心力,只要正确运用牛顿第二定律和万有引力定律列式求解即可。
例6:假设火星和地球都是球体,火星的质量M火和地球质量M地之比M火/M地=p,火星的半径R火和地球半径R地之比R火/R地=q,那么离火星表面R火高处的重力加速度和离地球表面R地高处的重力加速度之比等于多少?
[审题]解题时要明确以下二点:
2、必须区别开普勒第三行星定律中的常量K与万有引力定律中常量G的不同
(1)开普勒第三定律中的常量K:
开普勒第三定律中的常量K= r3/T2,对于行星与太阳的天体系统而言,常量K仅与太阳的质量有关而与行星的质量无关。此规律对于其它的由‘中心天体’与‘环绕天体’组成的天体系统同样适用。常量K仅由‘中心天体’的质量决定而与‘环绕天体’的质量无关。‘中心天体’相同的天体系统中的常量K相同,‘中心天体’不同的天体系统的常量K也不同。“K= r3/T2=常量”的伟大意义在于启发牛顿总结、发现了万有引力定律。
(2)万有引力定律中的常量G:
万有引力定律中的常量G是由万有引力定律F= 变形求出的,G=F r2/m1m2,数值是G=6。67×10-11Nm2/Kg2.是卡文迪许扭秤实验测出的,适用于宇宙间的所有物体。万有引力定律中的常量G的测定不仅证明了万有引力的存在,更体现了万有引力定律在天文研究中的巨大价值。
变形求出的,G=F r2/m1m2,数值是G=6。67×10-11Nm2/Kg2.是卡文迪许扭秤实验测出的,适用于宇宙间的所有物体。万有引力定律中的常量G的测定不仅证明了万有引力的存在,更体现了万有引力定律在天文研究中的巨大价值。
(3)常量K与常量G的关系:
常量K与常量G有如下关系,K= GM/4π2,或者G=4π2/GM。K的值由‘中心天体’的质量而定,而常量G则是一个与任何因素无关的普适常量。
例3:行星绕太阳运转的轨道是椭圆,这些椭圆在一般情况下可以近似视为圆周轨道,试用万有引力定律和向心力公式证明对所有绕太阳运转的行星,绕太阳公转轨道半径的立方与运转周期的平方的比值为常量。论述此常量的决定因素有哪些?此结论是否也适用于地球与月球的系统? [审题] 本题中行星绕太阳运转的轨道近似视为圆周轨道时,只要运用万有引力定律和向心力公式即可证明得出结论。
[解析] 因为行星绕太阳运转需要的向心力是由太阳的万有引力提供,设太阳质量为M,行星的质量为m,行星绕太阳运转轨道的半径为r,运行周期为T,则,
GMm/r2=m4π2r/T2,故,r3/T2=GM/4π2,即,K= GM/4π2。
显然,由于太阳质量一定,K的数值仅由太阳质量M决定,与其它因素无关。这一结论适用于地球与月球系统,也适用于其它‘中心天体’与‘环绕天体’组成的天体系统。
 [总结]开普勒第三定律中的常量K与万有引力定律中的常量G的这种关系(K= GM/4π2,或者G=4π2/GM)可以用来方便的求解卫星类的问题,作为一种解题的‘切入口’应在解题过程中予以重视。
[总结]开普勒第三定律中的常量K与万有引力定律中的常量G的这种关系(K= GM/4π2,或者G=4π2/GM)可以用来方便的求解卫星类的问题,作为一种解题的‘切入口’应在解题过程中予以重视。
1、必须区别开普勒行星运动定律与万有引力定律的不同
开普勒行星运动定律
开普勒第一定律:所有行星围绕太阳运动的轨道均是椭圆,太阳处在这些椭圆轨道的一个公共焦点上。
开普勒第二定律(面积定律):太阳和运动着的行星之间的联线,在相等的时间内扫过的面积总相等。 开普勒第三定律(周期定律):各个行星绕太阳公转周期的平方和它们的椭圆轨道的半长轴的立方成正比。若用r表示椭圆轨道的半长轴,用T表示行星的公转周期,则有k=r3/T2是一个与行星无关的常量。 开普勒总结了第谷对天体精确观测的记录,经过辛勤地整理和计算,归纳出行星绕太阳运行的三条基本规律。开普勒定律只涉及运动学、几何学方面的内容。开普勒定律为万有引力定律的提出奠定了理论基础,此三定律也是星球之间万有引力作用的必然结果。
(2)万有引力定律
万有引力定律的内容是:
宇宙间一切物体都是相互吸引的,两个物体间的引力大小,跟它们的质量的乘积成正比,跟它们间的距离的平方成反比。
万有引力定律的公式是:
F=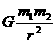 ,
(G=6.67×10-11牛顿·米2/千克2,叫作万有引力恒量)。
,
(G=6.67×10-11牛顿·米2/千克2,叫作万有引力恒量)。
万有引力定律的适用条件是:
严格来说公式只适用于质点间的相互作用,当两个物体间的距离远远大于物体本身大小时公式也近似适用,但此时它们间距离r应为两物体质心间距离。
(3)开普勒行星运动定律与万有引力定律的关系:
万有引力定律是牛顿根据行星绕太阳(或恒星)运动的宇宙现象推知行星所需要的向心力必然是由太阳对行星的万有引力提供,进而运用开普勒行星运动定律推导发现了万有引力定律. 开普勒行星运动定律是万有引力定律的理论基础。
开普勒行星运动定律从轨道形状、运动速度、转动周期、轨道半径等方面描述、揭示了行星绕太阳(或恒星)运动的宇宙现象,表明了天体运动运动学特征和规律。万有引力定律是从行星转动所需要的向心力来源与本质上揭示了行星与太阳(或恒星)以及宇宙万物间的引力关系,描述的是行星运动的动力学特征与规律。
例1:世界上第一颗人造地球卫星环绕地球运行轨道的长轴比第二颗人造地球卫星环绕地球轨道的长轴短8000km, 第一颗人造地球卫星环绕地球运转的周期是96.2min,求第一颗人造地球卫星环绕地球轨道的长轴和第二颗人造地球卫星环绕地球运转的周期(已知地球质量M=5.98X1024kg).
[审题]本题中第一颗人造地球卫星环绕地球轨道的长轴与第二颗人造地球卫星环绕地球运转的周期均是待求量,仅由开普勒行星运动定律难以求解。因此可以假想有一颗近地卫星环绕地球运行,由万有引力提供向心力的关系求出引卫星的R3/T2,又由开普勒第三定律知,所有绕地球运行的卫星的r3/T2值均相等,只要把假想卫星的R3/T2题中的二卫星的r3/T2值相比较即可求得结论。
[解析]假想有一颗近地卫星环绕地球运行,由于万有引力提供向心力,则
GMm/R2=m4π2 R /T2 解之得 K= R3/T2=GM/4π2,
再设第一颗人造地球卫星环绕地球轨道的长轴为a, 第二颗人造地球卫星环绕地球运转的周期为T,由开普勒第三定律得 K =(a/2)3/T12 =(a/2+4000)3/T22
由以上二式得,a=1.47×107m. T2=96.3 min.
[总结]由于此题中有两个待求物理量,单纯地运用万有引定律或开普勒行星运动定律难以求解,故而联立两个定律合并求解。同时,再假想有一颗近地卫星环绕地球运行,由万有引力提供向心力的关系求出卫星的R3/T2,由开普勒第三定律得知所有绕地球运行的卫星的r3/T2值均相等,找出等量关系即可求解。这种‘虚拟’卫星的思路十分重要,也是此题求解的‘切入口’。
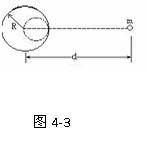 例2:如图4-3所示,在均匀球体中,紧贴球的边缘挖去一个半径为R/2的球形空穴后,对位于球心和空穴中心边线上、与球心相距d的质点m的引力是多大?
例2:如图4-3所示,在均匀球体中,紧贴球的边缘挖去一个半径为R/2的球形空穴后,对位于球心和空穴中心边线上、与球心相距d的质点m的引力是多大?
[解析] 把整个球体对质点的引力看成是挖去的小球体和剩余部分对质点的引力之和,即可求解完整的均质球体对球外质点m的引力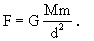
此引力可以看成是挖去球穴后的剩余部分对质点的引力F1与半径为R/2的小球对近质点的引力F2之和,即F=F1+F2。因为半径为R/2的小球质量M′=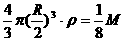 ;则
;则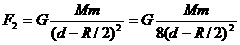 ,所以挖去球穴后的剩余部分对球外质点m的引力为:
,所以挖去球穴后的剩余部分对球外质点m的引力为:
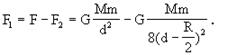
[总结]如果先设法求出挖去球穴后的重心位置,然后把剩余部分的质量集中于这个重心上,应用万有引力公式求解.这是不正确的.万有引力存在于宇宙间任何两个物体之间,但计算万有引力的简单公式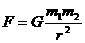 却只能适应于两个质点或均匀的球体。挖去空穴后的剩余部分已不再是均质球了,故不能直接使用上述公式计算引力。
却只能适应于两个质点或均匀的球体。挖去空穴后的剩余部分已不再是均质球了,故不能直接使用上述公式计算引力。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com