
题目列表(包括答案和解析)
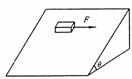
5、如图所示,一物块受到一个水平力F作永静止于斜面上,此力F的方向与斜面平行,如果将力F撤除,下泄对物块的描述正确的是( )
A.物块将沿斜面下滑
B.物块受到的摩擦力变大
C.物块立即获得加速度
D.物块所受的摩擦力方向改变
4、下列说法正解的是
A.牛顿发现万有引力定律并精确测出了引力常量
B.法拉第首先提出了场的概念,并用电场线和磁感线形象地描述电场和磁场
C.物理学中所有的物理量都是用比值法定义的
 D.弹力、摩擦力属于万有引力作用
D.弹力、摩擦力属于万有引力作用
3、 如图所示,AC是上端带定滑轮的固定竖直杆,质量不计的轻杆BC一端通过铰链固定在C点,另一端B悬挂一重为G的物体,且B端系有一根轻绳并绕过定滑轮A,用力F拉绳,开始时∠BCA>90°,现使∠BCA缓慢变小,直到杆BC接近竖直杆AC.此过程中,轻杆B端所受的力
如图所示,AC是上端带定滑轮的固定竖直杆,质量不计的轻杆BC一端通过铰链固定在C点,另一端B悬挂一重为G的物体,且B端系有一根轻绳并绕过定滑轮A,用力F拉绳,开始时∠BCA>90°,现使∠BCA缓慢变小,直到杆BC接近竖直杆AC.此过程中,轻杆B端所受的力
A.大小不变 B.逐渐增大
C.逐渐减小 D.先减小后增大
2、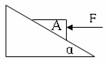 如图,重量为G的物体A在大小为F的水平向左恒力作用下,静止在倾角为α的光滑斜面上。下列关于物体对斜面压力N大小的表达式,不正确的是( )
如图,重量为G的物体A在大小为F的水平向左恒力作用下,静止在倾角为α的光滑斜面上。下列关于物体对斜面压力N大小的表达式,不正确的是( )
A.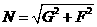 B.
B.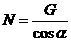
C.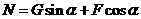 D.
D.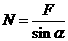
1、已知一些材料间的动摩擦因数如下表所示:
|
材料 |
木-金属 |
木-木 |
木-冰 |
钢-钢 |
|
动摩擦因数 |
0.20 |
0.30 |
0.03 |
0.25 |
质量为1.5kg的物块放置于某材料制作的水平面上,现用弹簧秤沿水平方向匀速拉此物块,读得弹簧秤的示数为3N,则关于两接触面的材料可能是(g取10m/s2)
(A)木-金属 (B)木-木 (C)钢-钢 (D)木-冰
5.物体的受力分析
例9:如图1-13甲所示,竖直墙壁光滑,分析静止的木杆受哪几个力作用。
[审题]首先选取研究对象--木杆,其次按顺序画力:①重力G-作用在木杆的中点,方向竖直向下;②画弹力。有两个接触点,墙与杆接触点属点面接触,弹力垂直于墙且指向杆,地与杆的接触点也属点面接触,杆受的弹力垂直于地面且指向杆;③画摩擦力。竖直墙光滑,墙与杆接触点没有摩擦力;假设地面光滑,杆将会向右运动,所以杆静止时有相对地面向右的运动趋势,所以地面对杆有向左的摩擦力。
[解析]杆受重力G、方向竖直向下;弹力N1,垂直于墙且指向杆,弹力N2,垂直于地面且指向杆;地面对杆向左的摩擦力f。如图1-13乙所示
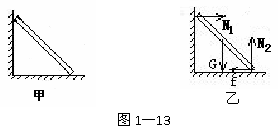
[总结]受力分析时应按步骤分析,杆受的各力应画在实际位置上。不要将各力的作用点都移到重心上去。
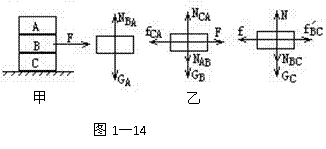
例10:如图1-14甲所示,A、B、C叠放于水平地面上,加一水平力F,三物体仍静止,分析A、B、C的受力情况。
[审题]用隔离法分析:先取A为研究对象:A受向下的重力GA、B对A的支持力NBA。假设B对A有水平方向的摩擦力,不论方向水平向左还是向右,都与A处的静止状态相矛盾,所以B对A没有摩擦力。取B为研究对象:B受向下的重力GB、A对B的压力NAB、C对B的支持力
NCB、水平力F。因B处静止,水平方向受合力为零,根据平衡条件,C对B一定有水平向左的摩擦力fCB。再取C为研究对象:C受向下的重力GC、B对C的压力NBC,地面对C的支持力N,由牛顿第三定律得,B对C的摩擦力向右,因C处静止合力为零,根据平衡条件,地对C的摩擦力f一定水平向左。
[解析]A、B、C三物体的受力如图图1-14乙所示
[总结]用隔离法分析物体受力分析最常用的方法,分析时应将研究的物体单独拿出来,不要都画在一起,以免出现混乱。同时应根据牛顿第三定律分析。A对B的压力及B对C的压力应以NAB和NBC表示,不要用GA和GB表示,因中它们跟GA、、GB是不同的。此题也可以用先整体后部分,由下向上的方法分析。
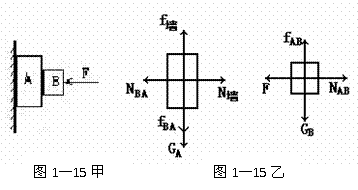
例11:如图1-15甲所示,物体A、B静止,画出A、B的受力图。
[审题]用隔离法分析。先隔离B:B受重力GB,外力F,由于F的作用,B和A之间的挤压,所以A对B有支持力NAB,假设A、B接触面光滑,物体B将相对A下滑,所以B有相对A向下的运动趋势,B受A向上的静摩擦力fAB。再隔离A:A受重力GA,墙对A的支持力N墙,由牛顿第三定律得,A受到B对它的压力NBA,水平向左,摩擦力fBA,方向竖直向下。假设墙是光滑的,A物体相对墙将下滑,也就是说A物体相对墙有向下的运动趋势,所以墙对A有竖直向上的摩擦力f墙。
[解析]A、B受力如图1-15乙所示
总结:此类问题用隔离法分析,应注意A、B间、A与墙间的摩擦力的分析,同时要根据牛顿第三定律分析。
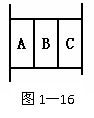 例12:如图1-16所示,用两相同的夹板夹住三个重为G的物体A、B、C,三个物体均保持静止,请分析各个物体的受力情况.
例12:如图1-16所示,用两相同的夹板夹住三个重为G的物体A、B、C,三个物体均保持静止,请分析各个物体的受力情况.
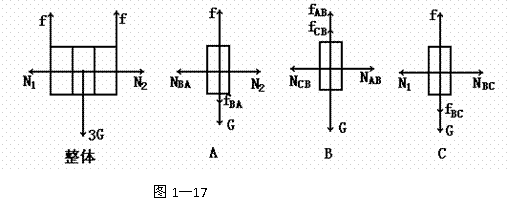
[审题]要分析各物体的受力情况,关键是分析A、B间、B、C间是否有摩擦力,所以可用先整体后隔离的方法。首先以三物体为一整体。竖直方向上,受重力3G,竖直向下,两板对它向上的摩擦力,分别为f;水平方向上,受两侧板对它的压力N1、N2。根据平衡条件得,每一侧受的摩擦力大小等于1.5G。然后再用隔离法分析A、B、C的受力情况,先隔离A,A物体受重力G,方向竖直向下,板对它的向上的摩擦力f,大小等于1.5G ,A物体要平衡,就必须受到一个B对它的向下的摩擦力fBA,根据平衡条件得,大小应等于0.5 G , 水平方向上,A物体受板对它的压力N1和B对它的压力NBA; 再隔离C,C物体的受力情况与A物体类似. 竖直方向上受重力G、板对它的向上的摩擦力f、B对它的向下的摩擦力fBC,水平方向上受板对它的压力N2、B对它的压力NBC。再隔离B,竖直方向上B物体受重力G 、由牛顿第三定律得,B受到A对它的向上的摩擦力fAB 、C对它的向上的摩擦力fCB ,以及水平方向上A对它的压力NAB和C对它的压力NCB。
[解析]A、B、C受力如图图1-17所示
[总结]明确各物体所受的摩擦力是解决此类问题的关键,较好的解决方法是先整体法确定两侧的摩擦力,再用隔离法确定单个物体所受的摩擦力。
例13:如图1-18所示,放置在水平地面上的直角劈M上有一个质量为m的物体,若m在其上匀速下滑,M仍保持静止,那么正确的说法是( )
 A.M对地面的压力等于(M+m)g
A.M对地面的压力等于(M+m)g
B.M对地面的压力大于(M+m)g
C.地面对M没有摩擦力
D.地面对M有向左的摩擦力
[审题]先用隔离法分析。先隔离m,m受重力mg、斜面对它的支持力N、沿斜面向上的摩擦力f,因m沿斜面匀速下滑,所以支持力N和沿斜面向上的摩擦力f可根据平衡条件求出。。再隔离M,M受竖直向下重力Mg、地面对它竖直向上的支持力N地、由牛顿第三定律得,m对M有垂直斜面向下的压力N'和沿斜面向下的摩擦力f',M相对地面有没有运动趋势,关键看f'和N'在水平方向的分量是否相等,若二者相等,则M相对地面无运动趋势,若二者不相等,则M相对地面有运动趋势,而摩擦力方向应根据具体的相对运动趋势的方向确定。
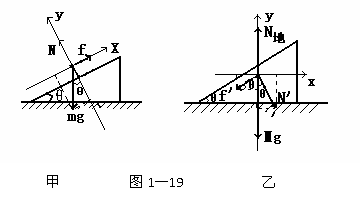 [解析]m、M的受力如图1-19所示
[解析]m、M的受力如图1-19所示
对m:建系如图甲所示,因m沿斜面匀速下滑,由平衡条件得:支持力N=mgcosθ,摩擦力f=mgsinθ
对M:建系如图乙所示,由牛顿第三定律得,N= N',f= f',在水平方向上,压力N'的水平分量N'sinθ= mgcosθsinθ,摩擦力f'的水平分量f'cosθ= mgsinθcosθ,可见f'cosθ=N'sinθ,所以M相对地面没有运动趋势,所以地面对M没有摩擦力。
在竖直方向上,整体平衡,由平衡条件得:N地= f'sinθ+ N'cosθ+Mg=mg+Mg。所以正确答案为:A、C
再以整体法分析:M对地面的压力和地面对M的支持力是一对作用力和反作用力,大小相等,方向相反。而地面对M的支持力、地面对M摩擦力是M和m整体的外力,所以要讨论这两个问题,可以整体为研究对象。整体在竖直方向上受到重力和支持力,因m在斜面上匀速下滑、M静止不动,即整体处于平衡状态,所以竖直方向上地面对M的支持力等于重力,水平方向上若受地面对M的摩擦力,无论摩擦力的方向向左还是向右,水平方向上整体都不能处于平衡,所以整体在水平方向上不受摩擦力。
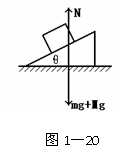
[解析]整体受力如图1-20所示,正确答案为:A、C。
[总结]综上可见,在分析整体受的外力时,以整体为研究对象分析比较简单。也可以隔离法分析,但较麻烦,在实际解题时,可灵活应用整体法和隔离法,将二者有机地结合起来。
总之,在进行受力分析时一定要按次序画出物体实际受的各个力,为解决这一难点可记忆以下受力口诀:,
地球周围受重力
绕物一周找弹力
考虑有无摩擦力
其他外力细分析
合力分力不重复
只画受力抛施力
4.摩擦力的方向
摩擦力的方向为与接触面相切,.与物体间的相对运动方向或相对运动趋势的方向相反。但相对运动趋势不如相对运动直观,具有很强的隐蔽性,常用下列方法判断。
法1:“假设法”。即假设接触面光滑,看原来相对静止的物体间能发生怎样的相对运动。若能发生,则这个相对运动的方向就为原来静止时两物体间的相对运动趋势的方向。若不能发生,则物体间无相对运动趋势。
例6:如图1-9所示为皮带传送装置,甲为主动轮,传动过程中皮带不打滑,P、Q分别为两轮边缘上的两点,下列说法正确的是:
A.P、Q两点的摩擦力方向均与轮转动方向相反
B.P点的摩擦力方向与甲轮的转动方向相反,Q点的摩擦力方向与乙轮的转动方向相同
C.P点的摩擦力方向与甲轮的转动方向相同,Q点的摩擦力方向与乙轮的转动方向相反
D.P、Q两点的摩擦力方向均与轮转动方向相同
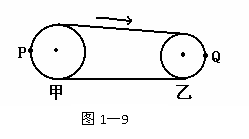
[审题]本题可用“假设法”分析。由题意可知甲轮与皮带间、乙轮与皮带间均相对静止,皮带与轮间的摩擦力为静摩擦力。假设甲轮是光滑的,则甲轮转动时皮带不动,轮上P点相对于皮带向前运动,可知轮上P点相对于皮带有向前运动的趋势,则轮子上的P点受到的静摩擦力方向向后,即与甲轮的转动方向相反,再假设乙轮是光滑的,则当皮带转动时,乙轮将会静止不动,这时,乙轮边缘上的Q点相对于皮带向后运动,可知轮上Q点有相对于皮带向后运动的趋势,故乙轮上Q点所受摩擦力向前,即与乙轮转动方向相同。
[解析]正确答案为B
[总结]判断摩擦力的有、无及摩擦力的方向可采用“假设法”分析。摩擦力方向与物体间的相对运动方向或相对运动趋势的方向相反,但不一定与物体的运动方向相反,有时还与物体的运动方向相同。
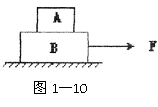 例7:如图1-10所示,物体A叠放在物体B上,水平地面光滑,外力F作用于物体B上使它们一起运动,试分析两物体受到的静摩擦力的方向。
例7:如图1-10所示,物体A叠放在物体B上,水平地面光滑,外力F作用于物体B上使它们一起运动,试分析两物体受到的静摩擦力的方向。
[审题]本题中假设A、B间接触面是光滑的,当F使物体B向右加速时,物体A由于惯性将保持原来的静止状态,经很短时间后它们的相对位置将发生变化,即物体A相对B有向左的运动,也就是说在原来相对静止时,物体A相对于B有向左的运动趋势,所以A受到B对它的静摩擦力方向向右(与A的实际运动方向相同)。同理B相对A有向右运动的趋势,所以B受到A对它的静摩擦力方向向左(与B的实际运动方向相反)。
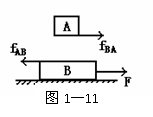
[解析]物体A相对于B有向左的运动趋势,所以A受到B对它的静摩擦力方向向右(与A的实际运动方向相同)。物体B相对A有向右运动的趋势,所以B受到A对它的静摩擦力方向向左(与B的实际运动方向相反)。如图1-11所示
法2:根据“物体的运动状态”来判定。
即先判明物体的运动状态(即加速度的方向),再利用牛顿第二定律(F=ma)确定合力,然后通过受力分析确定静摩擦力的大小和方向。
 例8:如图1-12所示,A、B两物体竖直叠放在水平面上,今用水平力F拉物体,两物体一起匀速运动,试分析A、B间的摩擦力及B与水平面间的摩擦力。
例8:如图1-12所示,A、B两物体竖直叠放在水平面上,今用水平力F拉物体,两物体一起匀速运动,试分析A、B间的摩擦力及B与水平面间的摩擦力。
[审题]本题分析摩擦力时应根据物体所处的运动状态。以A物体为研究对象:A物体在竖直方向上受重力和支持力,二者平衡,假设在水平方向上A受到B对它的静摩擦力,该力的方向一定沿水平方向,这样无论静摩擦力方向向左或向右,都不可能使A物体处于平衡状态,这与题中所给A物体处于匀速运动状态相矛盾,故A物体不受B对它的静摩擦力。反过来,B物体也不受A物体对它的静摩擦力。
分析B物体与水平面间的摩擦力可以A、B整体为研究对象。因A、B一起匀速运动,水平方向上合外力为零。水平方向上整体受到向右的拉力F作用,所以水平面对整体一定有向左的滑动摩擦力,而水平面对整体的滑动摩擦力也就是水平面对B物体的滑动摩擦力。
[解析]分析见上,因A匀速运动,所以A、B间无静摩擦力,又因A、B整体匀速运动,由平衡条件得,物体B受到水平面对它的滑动摩擦力应向左。
法3:利用牛顿第三定律来判定
此法关键是抓住“力是成对出现的”,先确定受力较少的物体受到的静摩擦力的方向,再确定另一物体受到的静摩擦力的方向。
例6中地面光滑,F使物体A、B一起向右加速运动,A物体的加速度和整体相同,由牛顿第二定律F=ma得A物体所受合外力方向一定向右,而A物体在竖直方向上受力平衡,所以水平方向上受的力为它的合外力,而在水平方向上只有可能受到B对它的静摩擦力,所以A受到B对它的静摩擦力方向向右。B对A的摩擦力与A对B的摩擦力是一对作用力和反作用力,根据牛顿第三定律,B受到A对它的静摩擦力方向向左。
[总结]静摩擦力的方向与物体间相对运动趋势方向相反,判断时除了用“假设法”外,还可以根据“物体的运动状态”、及 牛顿第三定律来分析。滑动摩擦力的方向与物体间相对运动的方向相反。
3.判断摩擦力的有、无
摩擦力的产生条件为:(1)两物体相互接触,且接触面粗糙;(2)接触面间有挤压;(3)有相对运动或相对运动趋势
例5:如图1-8所示,判断下列几种情况下物体A与接触面间有、无摩擦力。
图a中物体A静止
图b中物体A沿竖直面下滑,接触面粗糙
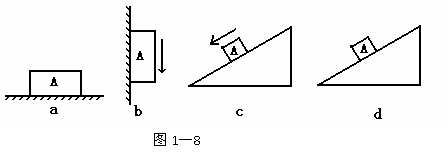 图c中物体A沿光滑斜面下滑
图c中物体A沿光滑斜面下滑
图d中物体A静止
[审题]图a中物体A静止,水平方向上无拉力,所以物体A与接触面间无相对运动趋势,所以无摩擦力产生;图b中物体A沿竖直面下滑时,对接触面无压力,所以不论接触面是否光滑都无摩擦力产生;图c中接触面间光滑,所以无摩擦力产生;图d中物体A静止,由于重力作用,有相对斜面向下运动的趋势,所以有静摩擦力产生。
[解析]图a、图b、图c中无摩擦力产生,图d有静摩擦力产生。
[总结]判断摩擦力的有、无,应依据摩擦力的产生条件,关键是看有没有相对运动或相对运动趋势。
2.弹力的方向
弹力是发生弹性形变的物体由于要恢复原状,而对它接触的物体产生的力的作用 。所以弹力的方向为物体恢复形变的方向。 平面与平面、点、曲面接触时,弹力方向垂直于平面,指向被压或被支持的物体;曲面与点、曲面接触时,弹力方向垂直于过接触点的曲面的切面,特殊的曲面,如圆面时,弹力方向指向圆心。弹力方向与重心位置无关。 绳子的弹力方向为:沿着绳子且指向绳子收缩的方向;且同一条绳子内各处的弹力相等 杆产生的弹力方向比较复杂,可以沿杆指向杆伸长或收缩的方向,也可不沿杆,与杆成一定的夹角。
例3:如图1-4所示,画出物体A 所受的弹力
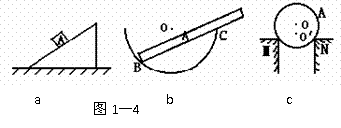
a图中物体A静止在斜面上
b图中杆A静止在光滑的半圆形的碗中
c图中A球光滑 O为圆心, O'为重心。
[审题]图a中接触处为面面接触,由于物体受重力作用,会对斜面斜向下挤压,斜面要恢复形变,应垂直斜面斜向上凸起,对物体有垂直斜面且指向物体斜向上的弹力。
图b中B处为点与曲面接触,发生的形变为沿半径方向向外凹,要恢复形变就得沿半径向上凸起,C处为点与平面接触, C处碗的形变的方向为斜向下压,要恢复形变就得沿垂直杆的方向向上,所以B处杆受的弹力为垂直过接触点的切面沿半径指向圆心,C处杆受的弹力为垂直杆向上。
图c中接触处为点与曲面接触,发生的形变均为沿半径分别向下凹,要恢复形变就得沿半径方向向上凸起,所以在M、N两接触处对A球的弹力为垂直过接触点的切面沿半径方向向上,作用线均过圆心O,而不过球的重心O'。
[解析]如图1-5所示
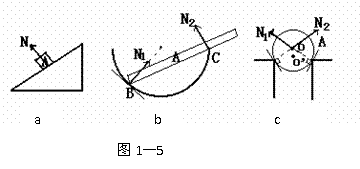
[总结]弹力的方向为物体恢复形变的方向。分析时首先应明确接触处发生的形变是怎样的,恢复形变时应向哪个方向恢复。另外应记住平面与平面、点、曲面接触,曲面与点、曲面接触,绳、杆弹力方向的特点,才能得以正确分析。 例4:如图1-6所示,小车上固定着一根弯成α角的曲杆,杆的另一端固定一个质量为m的球,试分析下列情况下杆对球的弹力的大小和方向:(1)小车静止;(2)小车以加速度a水平向右运动;(3)小车以加速度a水平向左运动。
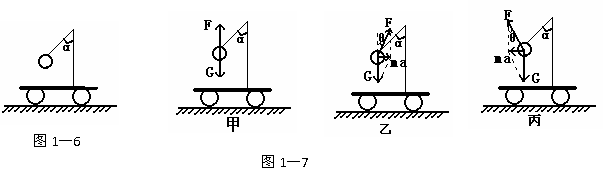
[审题]此题杆对球的弹力与球所处的运动状态有关。分析时应根据不同的运动状态具体分析。(1)小车静止时,球处于平衡状态,所受合外力为零,因重力竖直向下,所以杆对球的弹力F竖直向上,大小等于球的重力mg,如图1-7甲所示。
(2)当小车向右加速运动时,因球只受弹力和重力,所以由牛顿第二定律F=ma得,两力的合力一定是水平向右。由平行四边形法则得,杆对球的弹力F的方向应斜向右上方,设弹力F与竖直方向的夹角为θ,则由三角知识得:F= tanθ=a/g 如图1-7乙所示。
(3)当小车向左加速运动时,因球只受弹力和重力,所以由牛顿第二定律F=ma得,两力的合力一定是水平向左,由平行四边形法则得,杆对球的弹力F的方向应斜向左上方,设弹力F与竖直方向的夹角为θ,则由三角知识得:F= tanθ=a/g 如图1-7丙所示
可见,弹力的方向与小车运动的加速度的大小有关,并不一定沿杆的方向。
[解析](1)球处于平衡状态,杆对球产生的弹力方向竖直向上,且大小等于球的重力mg。
(2)当小车向右加速运动时,球受合力方向一定是水平向右,杆对球的弹力方向应斜向右上方,与小车运动的加速度的大小有关,其方向与竖直杆成arctan a/g角,大小等于。(3)当小车向左加速运动时,球受合力方向一定是水平向左,杆对球的弹力方向应斜向左上方,与小车运动的加速度的大小有关,其方向与竖直杆成arctan a/g角,大小等于。
[总结]杆对球的弹力方向不一定沿杆,只有当加速度向右且a= gtanθ时,杆对小球的弹力才沿杆的方向,所以在分析物体与杆固定连接或用轴连接时,物体受杆的弹力方向应与运动状态对应并根据物体平衡条件或牛顿第二定律求解。
1.弹力有、无的判断
弹力的产生条件是接触且发生弹性形变。但有的形变明显,有的不明显。那么如何判断相互接触的物体间有无弹力?
法1: “假设法”,即假设接触物体撤去,判断研究对象是否能维持现状。若维持现状则接触物体对研究对象没有弹力,因为接触物体使研究对象维持现状等同于没有接触物,即接触物形同虚设,故没有弹力。若不能维持现状则有弹力,因为接触物撤去随之撤去了应该有的弹力,从而改变了研究对象的现状。可见接触物对研究对象维持现状起着举足轻重的作用,故有弹力。
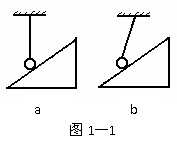 例1:如图所示,判断接触面对球有无弹力,已知球静止,接触面光滑。
例1:如图所示,判断接触面对球有无弹力,已知球静止,接触面光滑。
[审题]在a、b图中,若撤去细线,则球都将下滑,故细线中均有拉力, a图中若撤去接触面,球仍能保持原来位置不动,所以接触面对球没有弹力;b图中若撤去斜面,球就不会停在原位置静止,所以斜面对小球有支持力。
[解析]图a中接触面对球没有弹力;图b中斜面对小球有支持力
法2:根据“物体的运动状态”分析弹力。即可以先假设有弹力,分析是否符合物体所处的运动状态。或者由物体所处的运动状态反推弹力是否存在。总之,物体的受力必须与物体的运动状态符合。同时依据物体的运动状态,由二力平衡(或牛顿第二定律)还可以列方程求解弹力。
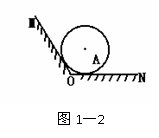 例2:如图所示,判断接触面MO、ON对球有无弹力,已知球静止,接触面光滑。
例2:如图所示,判断接触面MO、ON对球有无弹力,已知球静止,接触面光滑。
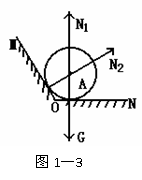 [审题]图中球由于受重力,对水平面ON一定有挤压,故水平面ON对球一定有支持力,假设还受到斜面MO的弹力,如图1-3所示,则球将不会静止,所以斜面MO对球没有弹力。
[审题]图中球由于受重力,对水平面ON一定有挤压,故水平面ON对球一定有支持力,假设还受到斜面MO的弹力,如图1-3所示,则球将不会静止,所以斜面MO对球没有弹力。
[解析]水平面ON对球有支持力,斜面MO对球没有弹力。
再如例1的a图中,若斜面对球有弹力,其方向应是垂直斜面且指向球,这样球也不会处于静止状态,所以斜面对球也没有弹力作用。
[总结]弹力有、无的判断是难点,分析时常用“假设法”并结合“物体的运动状态”分析。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com