
题目列表(包括答案和解析)
6、 在磁感应强度为B的匀强磁场中,有一与磁场方向垂直长度为L金属杆aO,已知ab=bc=cO=L/3,a、c与磁场中以O为圆心的同心圆(都为部分圆弧)金属轨道始终接触良好.一电容为C的电容器接在轨道上,如图所示,当金属杆在与磁场垂直的平面内以O为轴,以角速度ω顺时针匀速转动时:( )AC
在磁感应强度为B的匀强磁场中,有一与磁场方向垂直长度为L金属杆aO,已知ab=bc=cO=L/3,a、c与磁场中以O为圆心的同心圆(都为部分圆弧)金属轨道始终接触良好.一电容为C的电容器接在轨道上,如图所示,当金属杆在与磁场垂直的平面内以O为轴,以角速度ω顺时针匀速转动时:( )AC
A.Uac=2Ub0
B.Uac=2Uab
C.电容器带电量Q 
D.若在eO间连接一个电压表,则电压表示数为零
|

5、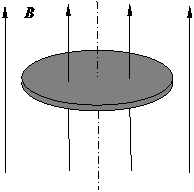 如图所示,一个金属薄圆盘水平放置在竖直向上的匀强磁场中,下列做法中能使圆盘中产生感应电流的是BD
如图所示,一个金属薄圆盘水平放置在竖直向上的匀强磁场中,下列做法中能使圆盘中产生感应电流的是BD
A.圆盘绕过圆心的竖直轴匀速转动
B.圆盘以某一水平直径为轴匀速转动
C.圆盘在磁场中向右匀速平移
D.匀强磁场均匀增加
4、 如图所示,金属棒ab置于水平放置的光滑框架cdef上,棒与框架接触良好,匀强磁场垂直于ab棒斜向下.从某时刻开始磁感应强度均匀减小,同时施加一个水平外力F使金属棒ab保持静止,则F C
如图所示,金属棒ab置于水平放置的光滑框架cdef上,棒与框架接触良好,匀强磁场垂直于ab棒斜向下.从某时刻开始磁感应强度均匀减小,同时施加一个水平外力F使金属棒ab保持静止,则F C
A. 方向向右,且为恒力
B.方向向右,且为变力
C.方向向左,且为变力
D.方向向左,且为恒力
3、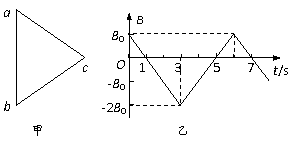 如图甲所示,正三角形导线框abc放在匀强磁场中静止不动,磁场方向与线框平面垂直,磁感应强度B随时间t的变化关系如图乙所示,t=0时刻,磁感应强度的方向垂直纸面向里.图丙中能表示线框的ab边受到的磁场力F随时间t的变化关系的是(力的方向规定以向左为正方向)A
如图甲所示,正三角形导线框abc放在匀强磁场中静止不动,磁场方向与线框平面垂直,磁感应强度B随时间t的变化关系如图乙所示,t=0时刻,磁感应强度的方向垂直纸面向里.图丙中能表示线框的ab边受到的磁场力F随时间t的变化关系的是(力的方向规定以向左为正方向)A
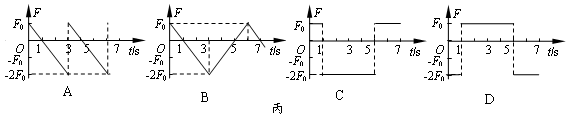
2、 如图甲所示,光滑导轨水平放置在与水平方向夹
如图甲所示,光滑导轨水平放置在与水平方向夹 角斜向下的匀强磁场中,匀强磁场的磁感应强度B随时间的变化规律如图乙所示(规定斜向下为正方向),导体棒ab垂直导轨放置,除电阻R的阻值外,其余电阻不计,导体棒ab在水平外力作用下始终处于静止状态。规定a→b的方向为电流的正方向,水平向右的方向为外力的正方向,则在0-t时间内,能正确反映流过导体棒ab的电流i和导体棒ab所受水平外力F随时间t变化的图象是( )D
角斜向下的匀强磁场中,匀强磁场的磁感应强度B随时间的变化规律如图乙所示(规定斜向下为正方向),导体棒ab垂直导轨放置,除电阻R的阻值外,其余电阻不计,导体棒ab在水平外力作用下始终处于静止状态。规定a→b的方向为电流的正方向,水平向右的方向为外力的正方向,则在0-t时间内,能正确反映流过导体棒ab的电流i和导体棒ab所受水平外力F随时间t变化的图象是( )D
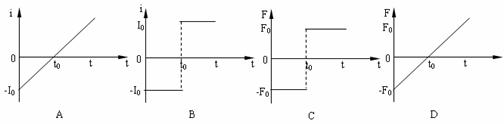
1、 电阻
电阻 、电容
、电容 与一线圈连成闭合电路,条形磁铁静止于线圈的正上方,
与一线圈连成闭合电路,条形磁铁静止于线圈的正上方, 极朝下,如图所示。现使磁铁自由下落,在
极朝下,如图所示。现使磁铁自由下落,在 极接近线圈上端的过程中,流过
极接近线圈上端的过程中,流过 的电流方向和电容器极板的带电情况是(
)D
的电流方向和电容器极板的带电情况是(
)D
 、从
、从 到
到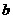 ,上极板带正电;
,上极板带正电;
 、从
、从 到
到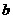 ,下极板带正电;
,下极板带正电;
 、从
、从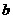 到
到 ,上极板带正电;
,上极板带正电;
 、从
、从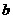 到
到 ,下极板带正电;
,下极板带正电;
85、如图所示,一个与平台连接的足够长斜坡倾角 ,一辆卡车的质量为1t。关闭发动机,卡车从静止开始沿斜坡滑下,最大速度可达120
,一辆卡车的质量为1t。关闭发动机,卡车从静止开始沿斜坡滑下,最大速度可达120 ,已知卡车运动过程中所受空气阻力和地面阻力与速度成正比,即
,已知卡车运动过程中所受空气阻力和地面阻力与速度成正比,即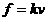 。
。
(1)求出比例系数k;
(2)现使卡车以恒定功率P沿斜坡向上行驶,达到的最大速度为54 ,求功率P;
,求功率P;
(3)当卡车开上平台后,继续保持此恒定功率行驶40s,重新匀速行驶,求卡车开上平台后到匀速行驶的过程中克服阻力所做的功。
解:(1)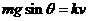 m(2分)
m(2分)
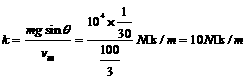 (2分)
(2分)
(2)因为 ,牵引力
,牵引力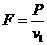 (1分)
(1分)
当卡车向上匀速行驶时: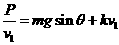 ,由此可得:
,由此可得:
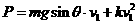 (2分)
(2分)  (1分)
(1分)
(3)卡车开上平台后,先加速后匀速,匀速行驶的最大速度为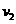 。
。
 (1分) 得
(1分) 得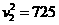
根据动能定理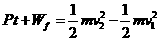 (4分)
(4分)
 (1分)
(1分)
84、 如图所示,可视为质点的三物块A、B、C放在倾角为300、长L=2m的固定斜面上,物块与斜面间的动摩擦因数μ=
如图所示,可视为质点的三物块A、B、C放在倾角为300、长L=2m的固定斜面上,物块与斜面间的动摩擦因数μ= ,A与B紧靠在一起,C紧靠在固定挡板上,三物块的质量分别为mA=0.80kg、mB=0.64kg、mC=0.50kg,其中A不带电,B、C的带电量分别为qB=+4.0×10-5C、qC=+2.0×10-5C且保持不变,开始时三个物块均能保持静止且与斜面间均无摩擦力作用.如果选定两点电荷在相距无穷远处的电势能为0,则相距为r时,两点电荷具有的电势能可表示为
,A与B紧靠在一起,C紧靠在固定挡板上,三物块的质量分别为mA=0.80kg、mB=0.64kg、mC=0.50kg,其中A不带电,B、C的带电量分别为qB=+4.0×10-5C、qC=+2.0×10-5C且保持不变,开始时三个物块均能保持静止且与斜面间均无摩擦力作用.如果选定两点电荷在相距无穷远处的电势能为0,则相距为r时,两点电荷具有的电势能可表示为 .现给A施加一平行于斜面向上的力F,使A在斜面上作加速度a=1.5m/s2的匀加速直线运动,经过时间t0,力F变为恒力,当A运动到斜面顶端时撤去力F.已知静电力常量k=9.0×109N·m2/C2,g=10m/s2.求:
.现给A施加一平行于斜面向上的力F,使A在斜面上作加速度a=1.5m/s2的匀加速直线运动,经过时间t0,力F变为恒力,当A运动到斜面顶端时撤去力F.已知静电力常量k=9.0×109N·m2/C2,g=10m/s2.求:
(1)未施加力F时物块B、C间的距离;
(2)t0时间内A上滑的距离;
(3)t0时间内库仑力做的功;
(4)力F对A物块做的总功.
解:(1)A、B、C处于静止状态时,设B、C间距离为L1,则C对B的库仑斥力
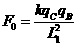 (1分)
(1分)
以A、B为研究对象,根据力的平衡 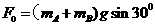 (1分)
(1分)
联立解得 L1=1.0m (1分)
(2)给A施加力F后, A、B沿斜面向上做匀加速直线运动,C对B的库仑斥力逐渐减小,A、B之间的弹力也逐渐减小.经过时间t0,B、C间距离设为L2,A、B两者间弹力减小到零,此后两者分离,力F变为恒力.则t0时刻C对B的库仑斥力为
 ① (1分)
① (1分)
以B为研究对象,由牛顿第二定律有
 ② (1分)
② (1分)
联立①②解得 L2=1.2m
则t0时间内A上滑的距离 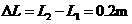 (1分)
(1分)
(3)设t0时间内库仑力做的功为W0,由功能关系有
 (1分)
(1分)
代入数据解得  ③ (1分)
③ (1分)
(4)设在t0时间内,末速度为v1,力F对A物块做的功为W1,由动能定理有
 ④ (1分)
④ (1分)
而  ⑤
⑤
 ⑥
⑥
 ⑦ (1分)
⑦ (1分)
由③~⑦式解得  J (1分)
J (1分)
经过时间t0后,A、B分离,力F变为恒力,对A由牛顿第二定律有
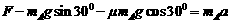 ⑧ (1分)
⑧ (1分)
力F对A物块做的功  ⑨
⑨
由⑧⑨式代入数据得  (1分)
(1分)
则力F对A物块做的功 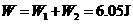 (1分)
(1分)
83、如图所示,一轻绳绕过无摩擦的两个轻质小定滑轮O1、O2和质量mB=m的小球连 接,另一端与套在光滑直杆上质量mA=m的小物块连接,已知直杆两端固定,与两定滑轮在同一竖直平面内,与水平面的夹角θ=60°,直杆上C点与两定滑轮均在同一高度,C点到定滑轮O1的距离为L,重力加速度为g,设直杆足够长,小球运动过程中不会与其他物体相碰.现将小物块从C点由静止释放,试求:
接,另一端与套在光滑直杆上质量mA=m的小物块连接,已知直杆两端固定,与两定滑轮在同一竖直平面内,与水平面的夹角θ=60°,直杆上C点与两定滑轮均在同一高度,C点到定滑轮O1的距离为L,重力加速度为g,设直杆足够长,小球运动过程中不会与其他物体相碰.现将小物块从C点由静止释放,试求:
(1)小球下降到最低点时,小物块的机械能(取C点所在的水平面为参考平面);
(2)小物块能下滑的最大距离;
(3)小物块在下滑距离为L时的速度大小.
解:(1)设此时小物块的机械能为E1.由机械能守恒定律得
 (3分)
(3分)
(2)设小物块能下滑的最大距离为sm,由机械能守恒定律有
 (2分)
(2分)
而 (1分)
(1分)
代入解得  (2分)
(2分)
(3)设小物块下滑距离为L时的速度大小为v,此时小球的速度大小为vB,则
 (1分)
(1分)
 (2分)
(2分)
解得  (2分)
(2分)
82、 如图所示,一质量m2=0.25kg的平顶小车,在车顶中间放一质量m3=0.1kg的小物体,小物体可视为质点,与车顶之间的动摩擦因数μ=
如图所示,一质量m2=0.25kg的平顶小车,在车顶中间放一质量m3=0.1kg的小物体,小物体可视为质点,与车顶之间的动摩擦因数μ= ,小车静止在光滑的水平轨道上.现有一质量m1=0.05kg的子弹以水平速度v0=20m/s射中小车左端,并留在车中(子弹与车相互作用时间很短).后来小物体m3以速度v3=1m/s从平顶小车的一端滑出,取g=10m/s2.试求:
,小车静止在光滑的水平轨道上.现有一质量m1=0.05kg的子弹以水平速度v0=20m/s射中小车左端,并留在车中(子弹与车相互作用时间很短).后来小物体m3以速度v3=1m/s从平顶小车的一端滑出,取g=10m/s2.试求:
(1)小物体m3从平顶小车的一端滑出时,平顶小车的速度大小;
(2)平顶小车的长度.
解:设子弹射中小车的瞬间,二者达到的共同速度为v1,当小物体从平顶小车滑出时,平顶小车的速度为v2,平顶小车的长度为L,由动量和能量守恒定律有
m1 v0=( m2+ m1 ) v1 (2分)
( m2+ m1 ) v1=( m2+ m1 ) v2+ m3 v3 (2分)
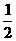 ( m2+ m1 )
( m2+ m1 ) -
-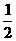 ( m2+ m1)
( m2+ m1) -
-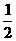 m3
m3 =μm3g
=μm3g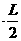 (2分)
(2分)
由上述三式代入数据解得 v2=3m/s (1分)
L=0.8m (2分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com