51、如图所示，在水平地面上固定一倾角θ=37°、表面光滑的斜面体，物体A以v₁=6m/s的初速度沿斜面上滑，同时在物体A的正上方，有一物体B以某一初速度水平抛出。如果当A上滑到最高点时恰好被B物体击中。(A、B均可看作质点， sin37°=0.6，cos37°=0.8，g取10m/s²)求：

　(1)物体A上滑到最高点所用的时间t；

　(2)物体B抛出时的初速度v₂；

　(3)物体A、B间初始位置的高度差h。

⑴物体A上滑过程中，由牛顿第二定律得：mgsinθ=ma

代入数据得：a=6m/s²(2分)

　　 设经过t时间相撞，由运动学公式：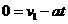

代入数据得：t=1s(2分)

⑵平抛物体B的水平位移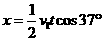：=2.4m(2分)

平抛速度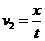：=2.4m/s(2分)

⑶物体A、B间的高度差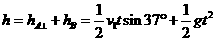：=6.8m(4分)

50、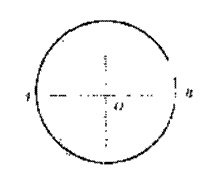如图所示，半径为R的光滑圆轨道竖直放置，长为2R的轻质杆两端各固定一个可视为质点的小球A、B，把轻杆水平放入圆形轨道内，若m,2m,m₀,m，重力加速度为g，现由静止释放两球，当轻杆到达竖直位置时，求：

　 (1)A、B两球的速度大小；

　 (2)A球对轨道的压力；

　 (3)要使轻杆到达竖直位置时，轻杆上刚好无弹力，A、B两球的质量应满足的条件。

答：

　 (1)设杆运动到竖直位置时，A、B两球的速度均为v₁ ………………(1分)

对AB系统机械能守恒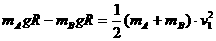：…………(2分)

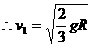　　 (1分)

　 (2)在竖直位置时，设杆对B球的强力为F_NB，轨道对A球的弹力为F_NA

对B球 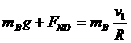　(1分)

………………(1分)

∴杆对B球有向上的支持力，对A球有向下压力

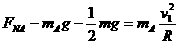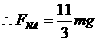对A球：　 (1分)

　 (1分)

由牛顿第三定律，知A球对轨道的压力为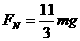　 (1分)

　 (2)要使轻杆到达竖直位置时，杆上恰好无弹力作用B球需满足

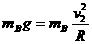　　 (1分)

对AB系统机械能守恒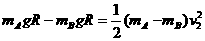

解得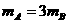

49、如图所示，长为L的细绳上端系一质量不计的环，环套在光滑水平杆上，在细线的下端吊一个质量为m的铁球(可视作质点)，球离地的高度h=L，当绳受到大小为3mg的拉力时就会断裂．现让环与球一起以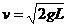的速度向右运动，在A处环被挡住而立即停止，A离右墙的水平距离也为L．不计空气阻力，已知当地的重力加速度为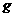．试求：

(1)在环被挡住而立即停止时绳对小球的拉力大小；

(2)在以后的运动过程中，球的第一次碰撞点离墙角B点的距离是多少？

(1)在环被挡住而立即停止后小球立即以速率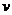绕A点做圆周运动，根据牛顿第二定律和圆周运动的向心力公式有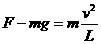：．．．．．．．．．．．．．2分

解得绳对小球的拉力大小为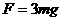：．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．1分

(2)根据上面的计算可知，在环被A挡住的瞬间绳恰好断裂，此后小球做平抛运动．

假设小球直接落到地面上，则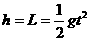：．．．．．．．．．．．．．．．．．．．．．．．．．1分

球的水平位移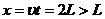：．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．1分

所以小球先与右边的墙壁碰撞后再落到地面上．．．．．．．．．．．．．．．．．．．．．．．．．．1分

设球平抛运动到右墙的时间为t′，则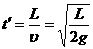．．．．．．．．．．．．．．．．．．．．．1分

小球下落的高度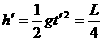．．．．．．．．．．．．．．．．．．．．．．．．．．．．．1分

所以球的第一次碰撞点距B的距离为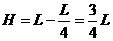：．．．．．．．．．．．．．．．1分

48、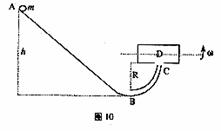如图10所示，质量为m可看作质点的小球从静止开始沿斜面由A点滑到B点后，进入与斜面圆滑连接的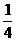竖直圆弧管道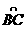，管道出口为C，圆弧半径R=15cm，AB的竖直高度差h=35cm. 在紧靠出口C处，有一水平放置且绕其水平轴线匀速旋转的圆筒(不计筒皮厚度)，筒上开有小孔D，筒旋转时，小孔D恰好能经过出口C处. 若小球射出C口时，恰好能接着穿过D孔，并且还能再从D孔向上穿出圆筒，小球返回后又先后两次向下穿过D孔而未发生碰撞. 不计摩擦和空气阻力，取g=10m/s²，问：

　 (1)小球到达C点的速度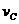为多少？

　 (2)圆筒转动的最大周期T为多少？

　 (3)在圆筒以最大周期T转动的情况下，要完成上述运动圆筒的半径R′必须为多少？

(1)对小球从A→C由机械能守恒定律得：

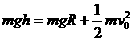　 ①　 …………2分

代入数值解出 v₀=2m/s

(2)小球向上穿出圆筒所用时间为t

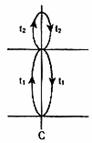
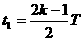　 　 (k=1，2，3……)　 ②　 ……2分

小球从离开圆筒到第二次进入圆筒所用时间为2t₂。

2t₂=nT　 (n=1，2，3……) ③　 ……2分

对小球由C竖直上抛的上升阶段，由速度公式得：

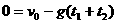　 ④　 …………2分

联立解得　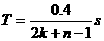 　　⑤　 …………1分

当n=k=1时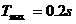，　 　…………1分

(3)对小球在圆筒内上升的阶段，由位移公式得：

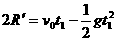　 ⑥　 …………2分

代入数值解得　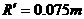 　　…………1分

47、一级方程式(F₁)汽车大赛中，冠军舒马赫驾驶着一辆总质量是M (M约1.5吨)的法拉利赛车经过一半径为R的水平弯道时的速度为v．工程师为提高赛车的性能，都将赛车形状设计得使其上下方空气存在一个压力差--气动压力(行业术语)，从而增大了赛车对地面的正压力，行业中将正压力与摩擦力的比值称为侧向附着系数，用η表示．为使上述赛车转弯时不致侧滑，则

(1)所需的向心力为多大？

(2)所需的摩擦力为多大？

(3)所需的气动压力为多大？

解：(1)由题义得赛车转弯时所需的向心力为：F = M ． (3分)

(2)赛车转弯时所需的向心力由地面的摩擦力提供，即f = F = M ．(3分)

　 　　　(3)设赛车受到的气动压力为N，受到地面的支持力为N′，则：

N′= N + Mg　 ．(3分)

　　　　　 　　由题知 　η = 　　　(2分)　　　　　

　　　 解得：N = ηM - Mg　 ． 　(3分)

46、如图所示，倾角θ=37°的斜面底端B平滑连接着半径r=0.40m的竖直光滑圆轨道。质量m=0.50kg的小物块，从距地面h=2.7m处沿斜面由静止开始下滑，小物块与斜面间的动摩擦因数μ=0.25，求：(sin37°=0.6，cos37°=0.8，g=10m/s²)

(1)物块滑到斜面底端B时的速度大小。

(2)物块运动到圆轨道的最高点A时，对圆轨道的压力大小。

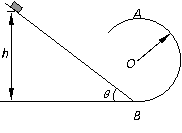
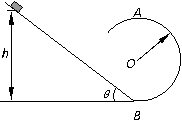解：(1)物块沿斜面下滑过程中，在重力、支持力和摩擦力作用下做匀加速运动，设下滑加速度为a ，到达斜面底端B时的速度为v，则

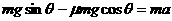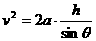　　　　 　(2分)

　　　　　 (2分)　　　　　　　　　　　　　　　

由①、②式代入数据解得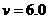：m/s (2分)　　　　　　　　　　　　　　

(2)设物块运动到圆轨道的最高点A时的速度为v_A，在A点受到圆轨道的压力为N，由机械能守恒定律得：

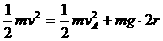　　　　　 (2分)

物块运动到圆轨道的最高点A时，由牛顿第二定律得：

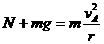　　　　　　　　　 (2分)

代入数据解得：　　 N=20N　　　　　　　　　　　 (1分)

由牛顿第三定律可知，物块运动到圆轨道的最高点A时，对圆轨道的压力大小

N_A=N=20N　　 (1分)

45、如图所示，质量为m的小球置于正方体的光滑盒子中，盒子的边长略大于球的直径．某同学拿着该盒子在竖直平面内做半径为R的匀速圆周运动，已知重力加速度为g，空气阻力不计，问：

(1)　 要使盒子在最高点时盒子与小球之间恰好无作用力，

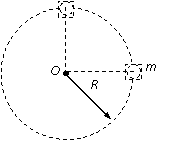则该盒子做匀速圆周运动的周期为多少？

(2) 若盒子以第(1)问中周期的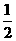做匀速圆周运动，

则当盒子运动到图示球心与O点位于同一水平面位置时，小球

对盒子的哪些面有作用力，作用力为多大？

解：(1)(共4分)设此时盒子的运动周期为T₀，因为在最高点时盒子与小球之间刚好无作用力，因此小球仅受重力作用．根据牛顿运动定律得：

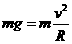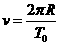　　　　　　 (1分)　　　　　　　

　　　　　　　　 (1分)

解之得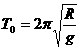：　　　　　　　　　 　 (2分)

(2)(共10分)设此时盒子的运动周期为T，则此时小球的向心加速度为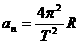： (1分)

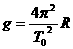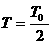由第一问知：　　　　　 且　　　　　　　　 (1分)

由上述三式知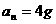：　　　　　　　　　　　　　　　 (1分)

设小球受盒子右侧面的作用力为F，受上侧面的作用力为N，根据牛顿运动定律知：

在水平方向上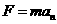：　 　　　　　　　　　　　　　　　　(2分)

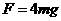即：　　　　　 　　　　　(1分)

在竖直方向上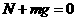：　　　　　　　　　　　　　 (2分)

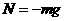即：　　　　　 　　　　　　　　　　(1分)

因为F为正值、N为负值，所以小球对盒子的右侧面和下侧面有作用力，分别为4 mg和mg　　　　　 　(1分)

44、如图所示，一水平放置的半径为r=0.5m的薄圆盘绕过圆心O点的竖直轴转动，圆盘边缘有一质量m=1.0kg的小滑块(可看成是质点)。当圆盘转动的角速度达到某一数值时，滑块从圆盘边缘滑落，滑块与圆盘间的动摩擦因数μ=0.2，圆盘所水平面离水平地面的高度h=2.5m，g取10m/s²．

(1)当圆盘的角速度多大时，滑块从圆盘上滑落？

(2)若取圆盘所在平面为零势能面，求滑块到达地面时的机械能；

(3)若落地点为C，求OC之间的距离．

解：(1)设圆盘的角速度为ω时，滑块从圆盘上滑落

μmg=mrω²-------------------------------------------------①

ω=2rad/s-------------------------------------------------②

(2)抛出时的动能：

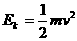= μmgr=0.1J------------------------------------③

平抛运动，只有重力做功，机械能守恒，滑块到达地面时的机械能

E=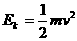=0.1J---------------------------------------------④

(3)滑块离开圆盘后做平抛运动，设水平位移为x，

x=vt----------------------------------------------------⑤

h= gt²------------------------------------------------⑥

∴ x = m----------------------------------------------⑦

由空间几何关系，得

OC==m-----------------------------------------⑧

评分说明：第一问4分，①②式各2分，第二问4分，③④式各2分，第三问6分，⑤⑥各1分，⑦⑧式各2分。

43、如图所示，将一根光滑的细金属棒折成V形，顶角为2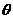，其对称轴竖直，在其中一边套上一个质量为m的小金属环P，

(1)若固定V形细金属棒，小金属环P从距离顶点O为 x的A点处由静止自由滑下，则小金属环由静止下滑至顶点O点时需多少时间？

(2)若小金属环P随V形细金属棒绕其对称轴以每秒n转匀速转动时，则小金属环离对称轴的距离为多少？

解：(1)设小环沿棒运动的加速度为a，由牛顿第二定律得

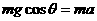　 　①　 (2分)

　　　 由运动学公式得

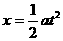　　 　②　 (2分)

由①②式得小环运动的时间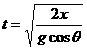　 ③　 (1分)　　　　　

　 (2)设小环离对称轴的距离为r，由牛顿第二定律得

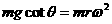　　 　　④　 (2分)

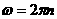　　 　⑤　 (2分)

由④⑤式得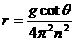 ⑥ (1分)

42、一质量为m的小物块沿半径为R的固定圆弧轨道下滑，滑到最低点时的速度是v，若小物块与轨道的动摩擦因数是μ，则当小物块滑到最低点时受到的摩擦力为： A

A．μm(g+v²/R)　B．μmv²/R　C．μmg　D．μmg(g-v²/R)