
题目列表(包括答案和解析)
33、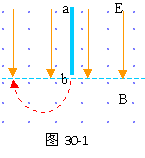 如图30-1所示,虚线上方有场强为E的匀强电场,方向竖直向下,虚线上下有磁感强度相同的匀强磁场,方向垂直纸面向外。ab是一根长L的绝缘细杆,沿电场线放置在虚线上方的场中,b端在虚线上。将一套在杆上的举正电小球从a端由静止释放后,小球先是加速运动,后是匀速运动则达b端。已知小球与绝缘杆间的动因摩擦数μ=0.3,小球的重力可忽略不计。当小球脱离杆进入虚线下方后,运动轨迹是半圆,圆半径为L/3。求:带电小球以 a到b运动过程中克服摩擦力做的功与电场力所做功的比值。
如图30-1所示,虚线上方有场强为E的匀强电场,方向竖直向下,虚线上下有磁感强度相同的匀强磁场,方向垂直纸面向外。ab是一根长L的绝缘细杆,沿电场线放置在虚线上方的场中,b端在虚线上。将一套在杆上的举正电小球从a端由静止释放后,小球先是加速运动,后是匀速运动则达b端。已知小球与绝缘杆间的动因摩擦数μ=0.3,小球的重力可忽略不计。当小球脱离杆进入虚线下方后,运动轨迹是半圆,圆半径为L/3。求:带电小球以 a到b运动过程中克服摩擦力做的功与电场力所做功的比值。
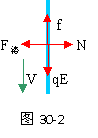 分析与解:(1)带电小球在沿杆向下运动时,
分析与解:(1)带电小球在沿杆向下运动时,
其受力情况如30-2图示。
水平方向:F洛=N=qBV [1]
竖直方向:qE=f [2] (匀速运动时)
又因f=μN [3],联立解[1][2][3]式得:qE=f=μqBVb
小球在磁场中作匀速圆周运动:qBVb=mVb2/R=3mVb2/L,所以Vb=qBL/3m
小球从a到b运动过程中,由动能定理:W电-Wf=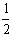 mVb2
mVb2
W电=qEL=μqBVbL=0.3×qBL(qBL/3m)=q2B2L2/10m
所以,Wf=W电-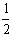 mVb2=q2B2L2/10m-(m/2)(q2B2L2/9m2)=2q2B2L2/45m
mVb2=q2B2L2/10m-(m/2)(q2B2L2/9m2)=2q2B2L2/45m
所以,Wf/W电=(2q2B2L2/45m)/(q2B2L2/10m)=4/9。
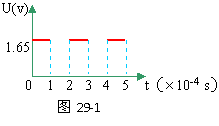
32、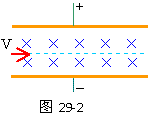 平行金属,板长1.4米,两板相距30厘米,两板间匀强磁场的B为1.3×10-3特斯拉,两板间所加电压随时间变化关系如29-1图所示。当t=0时,有一个a粒子从左侧两板中央以V=4×103米/秒的速度垂直于磁场方向射入,如29-2图所示。不计a粒子的重力,求:该粒子能否穿过金属板间区域?若不能,打在何处?若能,则需多长时间?
(已知a粒子电量q=3.2×10-19库,质量m=6.64×10-27千克)
平行金属,板长1.4米,两板相距30厘米,两板间匀强磁场的B为1.3×10-3特斯拉,两板间所加电压随时间变化关系如29-1图所示。当t=0时,有一个a粒子从左侧两板中央以V=4×103米/秒的速度垂直于磁场方向射入,如29-2图所示。不计a粒子的重力,求:该粒子能否穿过金属板间区域?若不能,打在何处?若能,则需多长时间?
(已知a粒子电量q=3.2×10-19库,质量m=6.64×10-27千克)
 分析与解:在t=0到t=1×10-4秒时间内,两板间加有电压,a粒子受到电场力和洛仑兹力分别为:F=qu/d=q×1.56/0.3=5.2q
方向竖直向下
分析与解:在t=0到t=1×10-4秒时间内,两板间加有电压,a粒子受到电场力和洛仑兹力分别为:F=qu/d=q×1.56/0.3=5.2q
方向竖直向下
f=qBv=q×1.3×10-3×4×103=5.2q 方向竖直向上
因F=f,故做匀速直线运动,其位移为:△S=v△t=4×103×1×10-4=0.4米
在t=1×10-4秒到t=2×10-4秒时间内,两板间无电场,a粒子在洛仑兹力作用下做匀速圆周运动,其轨迹半径为:
r=mv/qB=(6.64×10-27×4×103)/(3.2×10-19×1.3×10-3)=6.37×10-2米<d/4
所以粒子不会与金属板相碰。面a粒子做匀速圆周运动的周期为:
T=2πm/qB=(2×3.14×6.64×10-27)/(3.2×10-19×1.3×10-3)=1.0×10-4秒
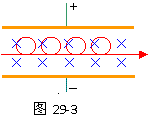
则在不加电压的时间内,a粒子恰好能在磁场中运动一周。当两板间又加上第2个周期和第3个周期的电压时,a粒子将重复上述的运动。故经13/4周期飞出板外(t=6.5×10-4秒)其运动轨迹如29-3图所示。
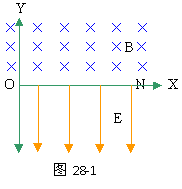
31、如图28-1所示,X轴上方有匀强磁场B,下方
有匀强电场E。电量为q、质量为m、重力不计的粒
子y轴上。X轴上有一点N(L.0),要使粒子在y轴
上由静止释放而能到达N点,问:(1)粒子应带何种
电荷? (2)释放点M应满足什么条件? (3)粒子从M
点运动到N点经历多长的时间?
分析与解:(1) 粒子由静止释放一定要先受电场力作用 (磁场对静止电荷没有作用力),所以 M点要在-Y轴上。要进入磁场必先向上运动,静上的电荷要向上运动必须受到向上的电场力作用,而场强 E方向是向下的,所以粒子带负电。
(2)粒子在M点受向上电场力,从静止出发做匀加速运动。在 O点进入匀强磁场后,只受洛仑兹力(方向沿+X轴)做匀速周围运动,经半个周期,回到X轴上的P点,进入匀强电场,在电场力作用下做匀减速直线运动直到速度为零。然后再向上做匀加速运动,在X轴上P点进入匀强磁场,做匀速圆运动,经半个周期回到X轴上的Q点,进入匀强电场,再在电场力作用下做匀减速运动直到速度为零。此后,粒子重复上述运动直到 X轴上的N点,运动轨迹如图28-2所示。
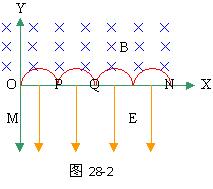 设释放点M的坐标为(0.-yO),在电场中由静
设释放点M的坐标为(0.-yO),在电场中由静
止加速,则:qEyO=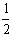 mV2 [1]
mV2 [1]
在匀强磁场中粒子以速率V做匀速圆周运动,
有:qBV=mV2/R [2]
设n为粒子做匀速圆周运动的次数(正整数)
则:L=n2R,所以R=L/2n [3]
解[1][2][3]式得:V=qBL/2mn,所以yO=qB2L2/8n2mE (式中n为正整数)
(3)粒子由M运动到N在电场中的加速运动和减速运动的次数为(2n-1)次,
每次加速或减速的时间都相等,设为t1,则:yO=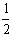 at12=
at12=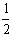 qEt12/m
qEt12/m
所以t1=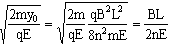
 粒子在磁场中做匀速圆周运动的半周期为t2,共n次,t2=πm/qB
粒子在磁场中做匀速圆周运动的半周期为t2,共n次,t2=πm/qB
粒子从M点运动到N点共经历的时间为:
t=(2n-1)t1+nt2=(2n-1)BL/2nE+nπm/qB (n=1、2、3……)
30、如图27-1所示,光滑导轨EF、GH等高平行放置,
EG间宽度为FH间宽度的3倍,导轨右侧水平且处于竖直向上的匀强磁场中,左侧呈弧形升高。ab、cd是质量均为m的金属棒,现让ab从离水平轨道h高处由静止下滑,设导轨足够长。试求:(1)ab、cd棒的最终速度,(2)全过程中感应电流产生的焦耳热。
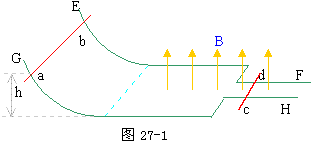 分析与解:ab下滑进入磁场后切割磁感线,在abcd电路中产生感应电流,ab、cd各受不同的磁场力作用而分别作变减速、变加速运动,电路中感应电流逐渐减小,当感应电流为零时,ab、cd不再受磁场力作用,各自以不同的速度匀速滑动。全过程中系统内机械能转化为电能再转化为内能,总能量守恒。
分析与解:ab下滑进入磁场后切割磁感线,在abcd电路中产生感应电流,ab、cd各受不同的磁场力作用而分别作变减速、变加速运动,电路中感应电流逐渐减小,当感应电流为零时,ab、cd不再受磁场力作用,各自以不同的速度匀速滑动。全过程中系统内机械能转化为电能再转化为内能,总能量守恒。
(1) ab自由下滑,机械能守恒:mgh=(1/2)mV2 [1]
由于ab、cd串联在同一电路中,任何时刻通过的电流总相等,金属棒有效长度 Lab=3Lcd,故它们的磁场力为:Fab=3Fcd [2]
在磁场力作用下,ab、cd各作变速运动,产生的感应电动势方向相反,当εab=εcd时,电路中感应电流为零,(I=0),安培力为零,ab、cd运动趋于稳定,此时有:BLabVab=BLcdVcd 所以Vab=Vcd/3 [3]
ab、cd受磁场力作用,动量均发生变化,由动量定理得:
Fab△t=m(V-Vab) [4] Fcd△t=mVcd [5]
联立以上各式解得:Vab=(1/10)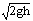 ,Vcd=(3/10)
,Vcd=(3/10)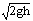
(2)根据系统能量守恒可得:Q=△E机=mgh-(1/2)m(Vab2+Vcd2)=(9/10)mgh
说 明:本题以分析ab、cd棒的受力及运动情况为主要线索求解。
注意要点:①明确ab、cd运动速度稳定的条件。
②理解电磁感应及磁场力计算式中的“L”的物理意义。
③电路中的电流、磁场力和金属棒的运动之间相互影响制约变化复杂, 解题时抓住每一瞬间存在Fab=3Fcd及终了状态时Vab=(1/3)Vcd的关系,用动量定理求解十分方便。
 ④金属棒所受磁场力是系统的外力,且Fab≠Fcd时,合力不为零,故系统动量不守恒,只有当Lab=Lcd时,Fab=Fcd,方向相反,其合力为零时,系统动
④金属棒所受磁场力是系统的外力,且Fab≠Fcd时,合力不为零,故系统动量不守恒,只有当Lab=Lcd时,Fab=Fcd,方向相反,其合力为零时,系统动
量才守恒。
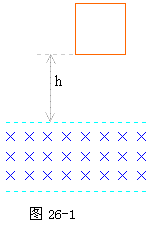
29、如图26-1所示,用密度为D、电阻率为ρ的导线做成正方形线框,从静止开始沿竖直平面自由下落。线框经过方向垂直纸面、磁感应强度为B的匀强磁场,且磁场区域高度等于线框一边之长。为了使线框通过磁场区域的速度恒定,求线框开始下落时的高度h。(不计空气阻力)
分析与解:线框匀速通过磁场的条件是受到的竖直向上的安培力与重力平衡,即:F安=mg [1]
设线框每边长为L,根据线框进入磁场的速度为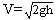 ,则安培力可表达为:
,则安培力可表达为:
F安=BIL=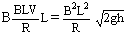 [2]
[2]
 设导线横截面积为S,其质量为:m=4LSD [3]
设导线横截面积为S,其质量为:m=4LSD [3]
其电阻为:R=ρ4L/S [4]
联立解[1]、[2]、[3]、[4]式得:
h=128D2ρ2g/B4
想一想:若线框每边长为L,全部通过匀强磁场的时间
为多少?(t=2L/V)
线框通过匀强磁场产生的焦耳热为多少?(Q=2mgL)
28、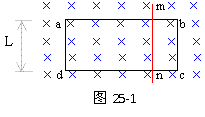 如图25-1所示为矩形的水平光滑导电轨道abcd,ab边和cd边的电阻均为5R0,ad边和bc边长均为L,ad边电阻为4R0,bc边电阻为2R0,整个轨道处于与轨道平面垂直的匀强磁场中,磁感强度为B。轨道上放有一根电阻为R0的金属杆mn,现让金属杆mn在平行轨道平面的未知拉力F作用下,从轨道右端以速率V匀速向左端滑动,设滑动中金属杆mn始终与ab、cd两边垂直,且与轨道接触良好。ab和cd边电阻分布均匀,求滑动中拉力F的最小牵引功率。
如图25-1所示为矩形的水平光滑导电轨道abcd,ab边和cd边的电阻均为5R0,ad边和bc边长均为L,ad边电阻为4R0,bc边电阻为2R0,整个轨道处于与轨道平面垂直的匀强磁场中,磁感强度为B。轨道上放有一根电阻为R0的金属杆mn,现让金属杆mn在平行轨道平面的未知拉力F作用下,从轨道右端以速率V匀速向左端滑动,设滑动中金属杆mn始终与ab、cd两边垂直,且与轨道接触良好。ab和cd边电阻分布均匀,求滑动中拉力F的最小牵引功率。
分析与解:mn金属杆从右端向左端匀速滑动切割磁感线产生感应电动势,mn相当于电源,其电路为内电路,电阻为内电阻。当外电阻最大时,即当mn滑到距离ad=(2/5)ab时,此时电阻Rmadn=Rmbcn=8R0时,外阻最大值Rmax=4R0,这时电路中电流最小值:Imin=ε/(Rmax+r)=BLV/(4R0+R0)=BLV/5R0
所以,Pmin=FminV=BLIminV=BLVBLV/5R0=B2L2V2/5R0
27、如图24-1所示,R1=R2=R3=R4=R,电键S闭合时,间距为d的平行板电容器C 的正中间有一质量为m,带电量为q的小球恰好处于静止状态;电键S断开时,小球向电容器一个极板运动并发生碰撞,碰撞后小球带上与极板同种性质的电荷。设碰撞过程中没有机械能损失,小球反弹后恰好能运动到电容器另一极板。若不计电源内阻,求:(1)电源的电动势,(2)小球与极板碰撞后的带电量。
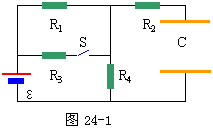 分析与解:(1)电键S闭合时,R1、R3并联与R4串联,(R2中没有电流通过)
分析与解:(1)电键S闭合时,R1、R3并联与R4串联,(R2中没有电流通过)
UC=U4=(2/3)ε
对带电小球有:mg=qE=qUC/d=(2/3)qε/d 得:ε=(3/2)mgd/q
(2)电键S断开后,R1、R4串联,则UC’=ε/2=(3/4)mgd/q [1]
小球向下运动与下极板相碰后,小球带电量变为q’,向上运动到上极板,全过程由动能定理得:mgd/2-qUC’/2-mgd+q’UC’=0 [2]
由[1][2]式解得:q’=7q/6。
26、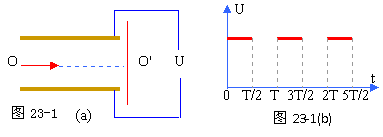 两平行金属板相距为d,加上如图23-1(b)所示的方波形电压,电压的最大值为U0,周期为T。现有一离子束,其中每个离子的质量为m,电量为q,从与两板等距处沿着与板平行的方向连续地射入两板间的电场中。设离子通过平行板所需的时间恰为 T(与电压变化周期相同),且所有离子都能通过两板间的空间打在右端的荧光屏上。试求:离子击中荧光屏上的位置的范围。(也就是与O‘点的最大距离与最小距离)。重力忽略不计。
两平行金属板相距为d,加上如图23-1(b)所示的方波形电压,电压的最大值为U0,周期为T。现有一离子束,其中每个离子的质量为m,电量为q,从与两板等距处沿着与板平行的方向连续地射入两板间的电场中。设离子通过平行板所需的时间恰为 T(与电压变化周期相同),且所有离子都能通过两板间的空间打在右端的荧光屏上。试求:离子击中荧光屏上的位置的范围。(也就是与O‘点的最大距离与最小距离)。重力忽略不计。
分析与解:
 各个离子在电场中运动时,其水平分运动都是匀速直线运动,而经过电场所需时间都是T,但不同的离子进入电场的时刻不同,由于两极间电压变化,因此它们的侧向位移也会不同。
各个离子在电场中运动时,其水平分运动都是匀速直线运动,而经过电场所需时间都是T,但不同的离子进入电场的时刻不同,由于两极间电压变化,因此它们的侧向位移也会不同。
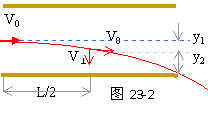
当离子在t=0,T,2T……时刻进入电场时,两板间在T/2时间内有电压U0,因而侧向做匀加速运动,其侧向位移为y1,速度为V。接着,在下一个T/2时间内,两板间没有电压,离子以V速度作匀速直线运动,侧向位移为y2,如图23-2所示。这些离子在离开电场时,侧向位移有最大值,即(y1+y2)。
 当离子在T=t/2,3/2T,5/2T……时刻进入电场
当离子在T=t/2,3/2T,5/2T……时刻进入电场
时,两板间电压为零,离子在水平方向做匀速
直线运动,没有侧向位移,经过T/2时间后,
两板间有电压U0,再经过T/2时间,有了侧向
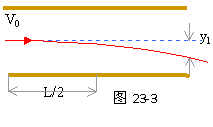
位移y1,如图23-3所示。这些离子离开电场时
有侧向位移的最小值,即y1。
当离子在上述两种特殊时刻之外进入电场的,其侧向位移值一定在(y1+y2)与y1之间。根据上述分析就可以求出侧向位移的最大值和最小值。
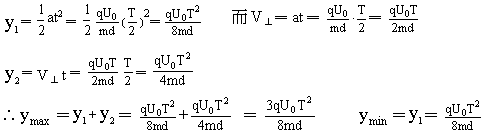
所以,离子击中荧光屏上的位置范围为:
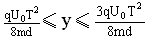
25、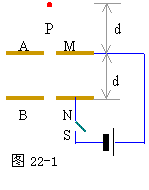 如图22-1所示,A、B为平行金属板,两板相距为d,分别与电源两极相连,两板的中央各有小孔M、N。今有一带电质点,自A板上方相距为d的P点由静止自由下落(P、M、N三点在同一竖直线上),空气阻力不计,到达N点时速度恰好为零,然后按原路径返回。若保持两板间的电压不变,则:
如图22-1所示,A、B为平行金属板,两板相距为d,分别与电源两极相连,两板的中央各有小孔M、N。今有一带电质点,自A板上方相距为d的P点由静止自由下落(P、M、N三点在同一竖直线上),空气阻力不计,到达N点时速度恰好为零,然后按原路径返回。若保持两板间的电压不变,则:
A. 若把A板向上平移一小段距离,质点自P点下落仍能返回。
B. 若把B板向下平移一小段距离,质点自P点下落仍能返回。
C. 若把A板向上平移一小段距离,质点自P点下落后将穿过N孔继续下落。
D. 若把B板向下平移一小段距离,质点自P点下落后将穿过N孔继续下落。
分析与解:当开关S一直闭合时,A、B两板间的电压保持不变,当带电质点从M向N运动时,要克服电场力做功,W=qUAB,由题设条件知:带电质点由P到N的运动过程中,重力做的功与质点克服电场力做的功相等,即:mg2d=qUAB
若把A板向上平移一小段距离,因UAB保持不变,上述等式仍成立,故沿原路返回,应选A。
若把B板下移一小段距离,因UAB保持不变,质点克服电场力做功不变,而重力做功增加,所以它将一直下落,应选D。
由上述分析可知:选项A和D是正确的。
想一想:在上题中若断开开关S后,再移动金属板,则问题又如何?(选A、B)。
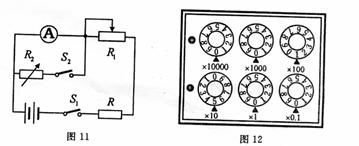
14.福建省龙岩二中2010届高三摸底考试用半偏法测量电流表的内阻,已知电流表满偏电流Ig=300μA,实验电路图如图11所示。
(1)部分实验步骤为:
A.按电路图接好电路,将R1、R2调节至最大
B.断开S2,闭合S1,调节R1,使表头指针 ;(1分)
C.闭合S2,调节R1,使表头指针 。(1分)
(2)上述实验步骤完成时,电阻箱R2的示数如图12所示,则电流表内阻rg=  。(1分)
。(1分)
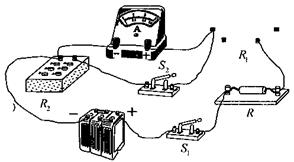
(3)按图11所示的电路,将图13中的器材连成实验电路。(2分)
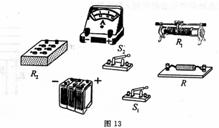
答案:(1)b 指向满刻度,
c指向满刻度的一半
(2)150 (3)如图(有错即不给这2分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com