5．如图所示，质量相同的两个带电粒子P、Q以相同的速度沿垂直于电场方向射入两平行板间的匀强电场中，P从两极板正中央射入，Q从下极板边缘射入，它们最后打在同一点(重力不计)，则从开始射入到打到上板的过程中

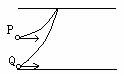A．它们运动的时间t_Q＞t_p　　　　　　

B．它们的电势能减小量之比ΔE_P：ΔE_Q=1：2

C．它们所带的电荷量之比q_p：q_Q=1：2　　

D．它们的动量增量之比Δp_P：Δp_Q=2：1

4．在竖直向上的匀强电场中，将一个带正电荷的小球，以某一初速竖直向上抛出，若小球电量不变，且不计阻力，则小球在上升过程中

A．动能一定增加　　　　　　　 B．电势能一定增加　　　

C．机械能一定增加　　　　　　 D．总能量一定增加

3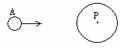．如图所示，P为金属球壳内的点，壳外一带负电体A移近金属球壳时，金属球壳内的P点处的场强E和电势ψ的变化是

A．E不变，ψ降低　　 B．E不变，ψ升高　　

C．E增大，ψ升高　　 D．E增大，ψ降低

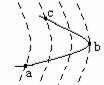
2．如图所示，a、b、c为电场中同一条水平方向电场线上的三点，c为ab中点，a、b电势分别为ψ_a=5V，ψ_b=3V。下列叙述正确的是

A．该电场在c点处的电势一定为4V　　　　

B．a点处的场强E_a一定大于b点处的场强

C．一正电荷从c点运动到b点电势能一定减少　　

D．一正电荷运动到c点时受到的电场力由c指向a

1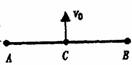．如图所示，A、B两点固定两个带电量绝对值相等的点电荷，在A、B连线的中点C处放一点电荷(不计重力)。若给该点电荷一个初速度V₀，V₀方向与AB连线垂直，则该点电荷可能的运动情况是

A．　 往复直线运动　　　　　　 　　　　　　　

B．匀速直线运动，电势能先增大后减小

C．加速度不断减小，速度不断增大的直线运动　

D．加速度先增大后减小，速度不断增大的直线运动

39.　如图36-1所示，A是一边长为l的正方形线框，电阻为R．现维持线框以恒定的速度v沿x轴运动，并穿过图中所示的匀强磁场B区域．取逆时针方向为电流正方向，线框从图示位置开始运动，则线框中产生的感应电流i随时间t变化的图线是图36-2中的：?［　 ］

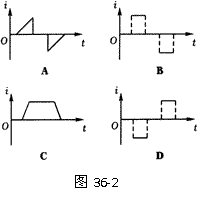解析：由于线框进入和穿出磁场时，线框内磁通量均匀变化，因此在线框中产生的感应电流大小不变．根据楞次定律可知，线框进入磁场时感应电流的方向与规定的正方向相同，穿出磁场时感应电流的方向与规定的正方向相反，因此应选B．

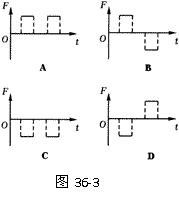想一想:若将题39改为：以x轴正方向作为力的正方向，则磁场对线框的作用力F随时间t的变化图线为图36-3中的：?［　 ］

同理可分析得正确答案应选C．

38.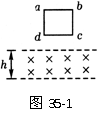　电阻为R的矩形导线框abcd，边长ab＝l、ad＝h、

质量为m，自某一高度自由落下，通过一匀强磁场，磁场方向垂

直纸面向里，磁场区域的宽度为h，如图35-1所示．若线框恰好

以恒定速度通过磁场，线框内产生的焦耳热是　　．(不考虑

空气阻力)

　解析：线框以恒定速度通过磁场，动能不变，重力势能减少，减少的重力势能转化为线框内产生的焦耳热．根据能的转化与守恒定律得：Q＝mg·2h＝2mgh．

37.如图34-1所示，AB、CD是两根足够长的固定平行金属导轨，两导轨间距离为l，导轨平面与水平面的夹角为θ．在整个导轨平面内都有垂直于导轨平面斜向上方的匀强磁场，磁感强度为B．在导轨的A、C端连接一个阻值为R的电阻．一根垂直于导轨放置的金属棒ab，质量为m，从静止开始沿导轨下滑．求ab棒的最大速度．(已知ab和导轨间的动摩擦因数为μ，导轨和金属棒的电阻不计)

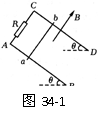解析：本题的研究对象为ab棒，画出ab棒的平面受力图，如图34-2．ab棒所受安培力F沿斜面向上，大小为F＝BIl＝B²l²v／R，则ab棒下滑的加速度

a＝［mgsinθ－(μmgcosθ+F)］／m．

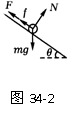ab棒由静止开始下滑，速度v不断增大，安培力F也增大，加速度a减小．当a＝0时达到稳定状态，此后ab棒做匀速运动，速度达最大．

mgsinθ－(μmgcosθ+B²l²v／R)＝0．

解得ab棒的最大速度

　v_m＝mgR(sinθ－μcosθ)／B²l²．

36.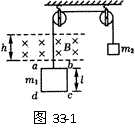如图33-1所示，线圈abcd每边长l＝0.20m，线圈质量m₁＝0.10kg、电阻R＝0.10Ω，砝码质量m₂＝0.14kg．线圈上方的匀强磁场磁感强度B＝0.5T，方向垂直线圈平面向里，磁场区域的宽度为h＝l＝0.20m．砝码从某一位置下降，使ab边进入磁场开始做匀速运动．求线圈做匀速运动的速度．

解析：该题的研究对象为线圈，线圈在匀速上升时受到的安培力F_安、绳子的拉力F和重力m₁g相互平衡，即

F＝F_安+m₁g．　①

砝码受力也平衡：

F＝m₂g．　②

线圈匀速上升，在线圈中产生的感应电流

I＝Blv／R，　③

因此线圈受到向下的安培力

F_安＝BIl．　④

联解①②③④式得v＝(m₂－m₁)gR／B²l²．

代入数据解得：v＝4(m／s)

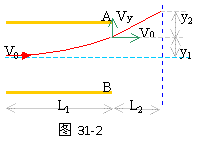
34、如图31-1所示，从阴极K射出的电子经U₀=5000V的电势差加速后，沿平行于板面的方向从中央射入两块长L₁=10cm，间距d=4cm的平行金属板AB之间。在离金属板边缘L₂=75cm处放置一个直径D=20cm，带有记录纸的圆筒。整个装置放在真空内，电子发射的初速度不计。

(1)若在金属板上加以U₁=1000V的直流电压(A板电势高)后，为使电子沿入射方向作匀速直线运动到达圆筒，应加怎样的磁场(大小和方向)；

(2)若在两金属板上加以U₂=1000cos2πtV的交流电压，并使圆筒绕中心轴按图示方向以n=2转/秒匀速转动。试确定电子在记录纸上的轨迹形状，并画出1秒钟内所记录到的图形。

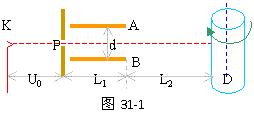分析与解：偏转极板上加恒定电压 U后，电子在电场中受到恒定的电场力作用，故所加的磁场方向只要使运动电子所受到的洛仑兹力与电场力等大反向即可。偏转极板上加上正弦交流电后，板间电场变为交变电场，电子在板间的运动是水平方向作匀速直线运动，竖直方向作简谐运动。偏出极板后作匀速直线运动，电子到达圆筒后，在筒上留下的痕迹是电子在竖直方向的“扫描”和圆筒匀速转动的合运动。

据动能定理：eU0=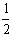mV0²，得电子加速后的入射速度为：

　V0=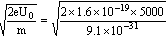 =4.2×10⁷m/s

(1)加直流电压时，A、B两板间场强：

　　E1=U1/d=1000/(4×10^-2)=2.5×10⁴v/m

为使电子作匀速直线运动，应使电子所受电场力与洛仑兹力平衡，即：qE1=qBV0，

得：B=E1/V0=(2.5×10⁴)/(4.2×10⁷)=6×10^-4T

方向为垂直于纸面向里。

(2)加上交流电压时，A、B两板间场强为：

E2=U2/d=1000cos2πt/(4×10^-2)=2.5×10⁴cos2πt v/m

电子飞离金属板时的偏距为：y₁=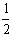at1²=(eE2/m)(L1/V0)²

电子飞离金属板时的竖直速度为：V_y=at₁=(eE2/m)(L1/V0)

从飞离板到到达筒的偏距：y₂=V_yt₂=(eE2/m)(L1/V0)(L2/V0)=(eE2L1L2)/(mV0²)

所以在纸筒上的落点对入射方向的总偏距为：(如图31-2所示)

y=y₁+y₂=(L1/2+L2)(eE2L1/mV0²)=(L1/2+L2)(L1U2/2U0d)

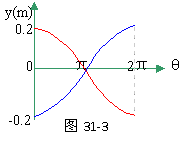　=(10/2+75)×10^-2×(10×1000cos2πt)/(2×5000×4)=0.20cos2πt m

可见，在记录纸上的点以振幅0.20m，周期T=2π/ω=1秒而作简谐运动。因圆筒每秒转2周(半秒转1周)，故在1秒内，纸上的图形如图31-3所示。

　35、如图32-1所示，两根互相平行、间距d=0.4米的金属导轨，水平放置于匀强磁场中，磁感应强度B=0.2T，磁场垂直于导轨平面，金属滑杆ab、cd所受摩擦力均为f=0.2N。两根杆电阻均为r=0.1Ω，导轨电阻不计，当ab杆受力F=0.4N的恒力作用时，ab杆以V₁做匀速直线运动，cd杆以V₂做匀速直线运动，求速度差(V₁－ V₂)等于多少？

分析与解：在电磁感应现象中，若回中的感应电动势是由导体做切割磁感线运动而产生的，则通常用ε=BlVsinθ来求ε较方便，但有时回路中的电动势是由几根棒同时做切割磁感线运动产生的，如果先求出每根导体棒各自的电动势，再求回路的总电动势，有时就会涉及“反电动势”而超纲。如果取整个回路为研究对象，直接将法拉第电磁感应定律ε=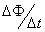用于整个回路上，即可“一次性”求得回路的总电动势，避开超纲总而化纲外为纲内。

cd棒匀速向右运动时，所受摩擦力f方向水平向左，则安培力F_cd方向水平向右，由左手定则可得电流方向从c到d，且有：

F_cd = IdB = f

I = f /Bd　　　　　　①

取整个回路abcd为研究对象，设回路的总电势为ε，由法拉第电磁感应定律ε=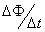，根据B不变，则△φ=B△S，在△t时间内，

△φ=B(V₁－V₂)△td

所以：ε=B(V₁－V₂)△td/△t=B(V₁－V₂)d　　　　 ②

又根据闭合电路欧母定律有：I=ε/2r　　　　 ③　　

由式①②③得：V₁－V₂ = 2fr / B²d²

代入数据解得：V₁－V₂ =6.25(m/s)