2．电磁场：按麦克斯韦的电磁场理论，变化电场和磁场总是相互联系的，形成一个不可分离的统一场，称为电磁场。电场和磁场只是这个统一的电磁场的两种具体表现。

理解电磁场是统一的整体：

根据麦克斯韦电磁场理论的两个要点：在变化的磁场的周围空间将产生涡漩电场，在变化的电场的周围空间将产生涡漩磁场．当变化的电场增强时，磁感线沿某一方向旋转，则在磁场减弱时，磁感线将沿相反方向旋转，如果电场不改变是静止的，则就不产生磁场．同理，减弱或增强的电场周围也将产生不同旋转方向的磁场．因此，变化的电场在其周围产生磁场，变化的磁场在其周围产生电场，一种场的突然减弱，导致另一种场的产生．这样，周期性变化的电场、磁场相互激发，形成的电磁场链一环套一环，如下图所示．需要注意的是，这里的电场和磁场必须是变化的，形成的电磁场链环不可能是静止的，这种电磁场是无源场(即：不是由电荷激发的电场，也不是由运动电荷-电流激发的磁场．)，并非简单地将电场、磁场相加，而是相互联系、不可分割的统一整体．在电磁场示意图中，电场E矢量和磁场B矢量，在空间相互激发时，相互垂直，以光速c在空间传播．

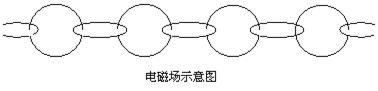
1．麦克斯韦的电磁场理论

(1)变化的磁场(电场)能够在周围空间产生电场(磁场)；

(2)均匀变化的磁场(电场)能够在周围空间产生稳定的电场(磁场)；

(3)振荡的磁场(电场)能够在周围空间产生同频率的振荡电场(磁场)；

可以证明：振荡电场产生同频率的振荡磁场；振荡磁场产生同频率的振荡电场。

点评：变化的磁场在周围激发的电场为涡旋电场，涡旋电场与静电场一样，对电荷有力的作用，但涡旋电场又于静电场不同，它不是静电荷产生的，它的电场线是闭合的，在涡旋电场中移动电荷时，电场力做的功与路径有关，因此不能引用“电势”、“电势能”等概念。另外要用联系的观点认识规律，变化的磁场产生电场是电磁感应的本质。

[例2]右图中，内壁光滑、水平放置的玻璃圆环内，有一直径略小于环口径的带正电的小球，正以速率v₀沿逆时针方向匀速转动。若在此空间突然加上竖直向上、磁感应强度B随时间成正比例增加的变化磁场，设小球运动过程中的电量不变，那么(　 CD　 )

A.小球对玻璃环的压力不断增大　 B.小球受到的磁场力不断增大

C.小球先沿逆时针方向做减速运动，过一段时间后，沿顺时针方向做加速运动

D.磁场力一直对小球不做功

分析：因为玻璃环所处有均匀变化的磁场，在周围产生稳定的涡旋电场，对带正电的小球做功，由楞次定律，判断电场方向为顺时针，在电场力的作用下，小球先沿逆时针方向做减速运动，过一段时间后，沿顺时针方向做加速运动。小球在水平面内沿轨迹半径方向受两个力：环的弹力N和磁场的洛仑兹力f，而且两个力的矢量和始终提供向心力，考虑到小球速度大小的变化和方向的变化以及磁场强弱的变化，弹力和洛仑兹力不一定始终在增大。洛仑兹力始终和运动方向垂直，所以磁场力不做功。正确为CD。

5、注意特殊点和过程

a.充电完毕和放电完毕时的特点

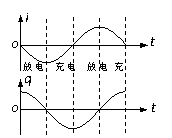b.充电过程和放电过程的特点

c.电场能和磁场能的转化的临界状态

d.电流在什么时候方向改变

[例1]　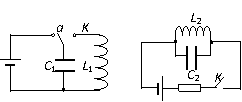　　　　　　　 右边两图中电容器的电容都是C=4×10^-6F，电感都是L=9×10^－4H，左图中电键K先接a，充电结束后将K扳到b；右图中电键K先闭合，稳定后断开。两图中LC回路开始电磁振荡t=3.14×10^－4s时刻，C₁的上极板正在____电(充电还是放电),带_____电(正电还是负电)；L₂中的电流方向向____(左还是右)，磁场能正在_____(增大还是减小)。]

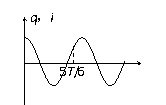解：先由公式求出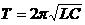=1.2π×10^－4s， t=3.14×10^－4s时刻是开始振荡后的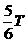。再看与左图对应的q-t图象(以上极板带正电为正)和与右图对应的i-t图象(以LC回路中有逆时针方向电流为正)，图象都为余弦函数图象。在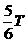时刻，从左图对应的q-t图象看出，上极板正在充正电；从右图对应的i-t图象看出，L₂中的电流向左，正在增大，所以磁场能正在增大。

4、分析电磁振荡要掌握以下三个要点(突出能量守恒的观点)：

⑴理想的LC回路中电场能E_电和磁场能E_磁在转化过程中的总和不变。

⑵回路中电流越大时，L中的磁场能越大(磁通量越大)。

⑶极板上电荷量越大时，C中电场能越大(板间场强越大、两板间电压越高、磁通量变化率越大)。

4、LC回路中的电流图象和电荷图象总是互为余函数。

3．LC回路的振荡周期和频率

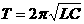
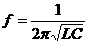
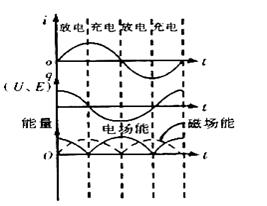
注意：(1)LC回路的T、f只与电路本身性质L、C有关

(2)电磁振荡的周期很小，频率很高，这是振荡电流与普通交变电流的区别。

2．LC回路的电磁振荡过程：可以用图象来形象分析电容器充、放电过程中各物理量的变化规律，如图所示[

1．振荡电路：大小和方向都随时间做周期性变儿的电流叫做振荡电流，能够产生振荡电流的电路叫振荡电路，LC回路是一种简单的振荡电路。

16、解析：设冰壶在未被毛刷擦过的冰面上滑行的距离为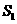，所受摩擦力的大小为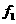：在 被毛刷擦过的冰面上滑行的距离为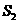，所受摩擦力的大小为。则有

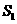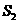+=S　 ①

式中S为投掷线到圆心O的距离。

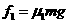　 ②

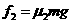　 ③

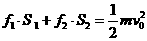设冰壶的初速度为，由功能关系，得　 ④

联立以上各式，解得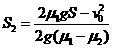　 ⑤

代入数据得

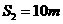　 ⑥

15、解析：设物块到达劈A的低端时，物块和A的的速度大小分别为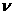和V，由机械能守恒和动量守恒得

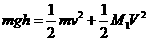　　　　 　　　　　　　　①

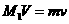　　　　 　　　　　　　　　　　　　②

设物块在劈B上达到的最大高度为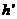，此时物块和B的共同速度大小为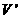，由机械能守恒和动量守恒得

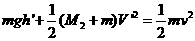　　　　 　　　　③

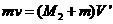　　　　 　　　　　　　　　　④

联立①②③④式得　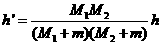　　　 　　　　　　　⑤

14、解析：⑴设AB碰撞后的速度为v₁,AB碰撞过程由动量守恒定律得

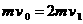
　　 设与C碰撞前瞬间AB的速度为v₂，由动能定理得

　 联立以上各式解得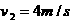

⑵若AB与C发生完全非弹性碰撞，由动量守恒定律得

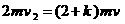
　 代入数据解得 　

　 此时AB的运动方向与C相同

若AB与C发生弹性碰撞，由动量守恒和能量守恒得

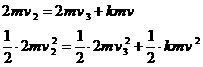
联立以上两式解得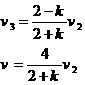

代入数据解得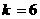　

此时AB的运动方向与C相反

若AB与C发生碰撞后AB的速度为0，由动量守恒定律得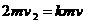

代入数据解得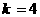

总上所述得　 当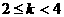时，AB的运动方向与C相同

当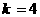时，AB的速度为0

　当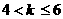时，AB的运动方向与C相反